几何体的展开图—人教版数学七（上）知识点训练
试卷更新日期：2024-10-15 类型：复习试卷
一、正方体的几种展开图的识别
-
1. 下列图形中（ ）可以折成正方体．A、
B、
C、
D、
2. 下列图形中，能围成正方体的是（ ）A、
B、
C、
D、
3. 有5个大小一样的正方形制成如图所示的拼接图形（阴影部分），请你在图中的拼接图形上再拼接一个正方形，使新拼接成的图形折叠后能成为一个封闭的正方体盒子，在如图所示的A，B，C，D四个位置中，能够选择的位置有（ ）
A、1个 B、2个 C、3个 D、4个4. 下列图形中可以作为一个正方体的展开图的是.
5. 小明同学设计了一个产品的正方体包装盒，如图所示，由于粗心少设计了其中一个顶盖，请你把它补上，使其成为一个两面均有盖的正方体盒子．
(1)、共有___________种弥补方法；(2)、任意画出一种成功的设计图（在图中补充）并将这些数字分别填入六个小正方形，使得折成的正方体相对面上的两个数相加得0（直接在图中填上即可）．二、含图案的正方体的展开图
-
6. 如图所示，正方体的展开图为（ ）
A、
B、
C、
D、
7. 一个正方体的六个面分别标有数字1，2，3，4，5，6，从三个不同的方向看到的情形如图1所示，图2为这个正方体的侧面展开图，则图中的x表示的数字是 ．
三、其它几何体的展开图
-
8. 下列选项中，是三棱柱的侧面展开图的为（ ）A、
B、
C、
D、
9. 如图所示的三棱柱的展开图不可能是（ ）
A、
B、
C、
D、
10. 如图是一个长方体包装盒，则它的平面展开图是（ ）
A、
B、
C、
D、
11. 如图，已知BC是圆柱底面的直径，AB是圆柱的高，在圆柱的侧面上，过点A，C嵌有一圈路径最短的金属丝，现将圆柱侧面沿AB剪开，所得的圆柱侧面展开图是（ ）
A、
B、
C、
D、
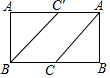12. 圆柱的侧面展开图是形．13. 画出如图所示的底面为直角三角形的直棱柱的表面展开图，并计算它的侧面积和表面积．
14. 如图（1），这是将一个棱长为1的正方体空盒子截去一个角后的剩下的几何体，请在图（2）的 的网格中画出它的一种展开图．
15. （1）如图所示的长方体，长、宽、高分别为4，3，6．若将它的表面沿某些棱剪开，展成一个平面图形，则下列图形中，可能是该长方体表面展开图的有________（填序号）．
（2）图A，B分别是题（1）中长方体的两种表面展开图，求得图A的外围周长为52，请你求出图B的外围周长．
（3）第（1）题中长方体的表面展开图还有不少，聪明的你能画出一个使外围周长最大的表面展开图吗？请画出这个表面展开图，并求出它的外围周长．
16. 某种包装盒的形状是长方体，长比高的三倍多2，宽的长度为3分米，它的展开图如图所示．（不考虑包装盒的黏合处）
(1)、设该包装盒的高为 ， 则该长方体的长为分米，边的长度为分米；（用含的式子表示）(2)、若的长为12分米，现对包装盒外表面涂色，每平方分米涂料的价格是6元，求为每个包装盒涂色的费用是多少？（注：包装盒内壁不涂色）17. 在学习《展开与折叠》这一课时，老师让同学们将准备好的正方体或长方体沿某些棱剪开，展开成平面图形．其中，阿中同学不小心多剪了一条棱，把一个长方体纸盒剪成了图①、图②两部分．根据你所学的知识，回答下列问题：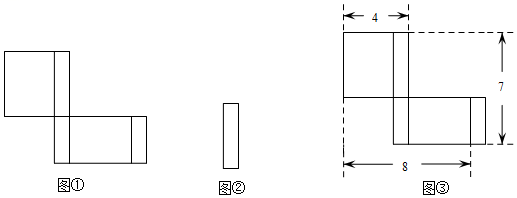
(1)、阿中总共剪开了几条棱？(2)、现在阿中想将剪断的图②重新粘贴到图①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，他有几种粘贴方法？请在图①上画出粘贴后的图形（画出一种即可）；(3)、已知图③是阿中剪开的图①的某些数据，求这个长方体纸盒的体积．四、由展开图判断几何体
-
18. 下列图形能折叠成圆锥的是（ ）A、
B、
C、
D、
19. 如图，是一个几何体的展开图，则该几何体是（ ）
A、长方体 B、圆柱 C、球 D、圆锥20. 下面是几个几何体的展开图，其中能围成棱锥的是（ ）A、
B、
C、
D、
21. 一个长方体的展开图如图所示，每个面分别标上的了1﹣6六个数字（数字在长方体的内侧），已知3、5、6三面面积之和是 ， 且5号面是一个边长3厘米的正方形．如果2号面是长方体底面，那么 号面是长方体上面，这样围成长方体后每相连两个面上的数字之和是质数（可重复）的有 组，这个长方体的体积是 ．
22.(1)、请写出下列展开图中对应几何体的名称：①；②；③ ．
(2)、图③中，侧面展开图的宽（较短边）为 ， 圆的半径为 ， 求图③所对应几何体的表面积．（结果保留π）23. 如图所示的平面图分别是由哪种几何体展开形成的？
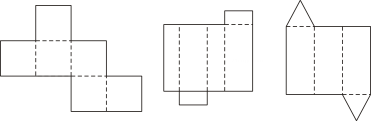
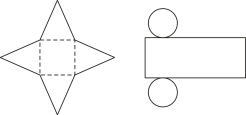
⑴ ▲ ；⑵ ▲ ；⑶ ▲ ；⑷ ▲ ；⑸ ▲ ；
24. 如图，左面的图形可能是右面哪些图形的展开图?
25. 下图是某几何体的表面展开图：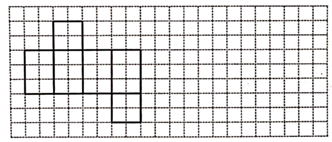
(1)、这个几何体的名称是；(2)、若该几何体的主视图是正方形，请在网格中画出该几何体的左视图、俯视图；(3)、若网格中每个小正方形的边长为1，则这个几何体的体积为.五、已知展开图进行几何体的相关计算
-
26. 如图所示的是一个长方体的表面展开图，其中四边形ABCD是正方形，根据图中标注的数据可求得原长方体的体积是.
27. 【综合与实践：】我们在“几何初步”这一章课题学习中探究了“如何制作长方体纸盒”，小明和小亮在课后对“如何制作正方体纸盒”又进行了探究：【动手操作：】小明用一张正方形的纸板按如图1所示的方式先在纸板四角剪去四个同样大小边长为的小正方形，再沿虚线折合起来就可以做成一个无盖的正方体纸盒．
小亮用一张长方形的纸板按如图2所示的方式先在纸板四角剪去两个同样大小的小正方形和两个同样大小的小长方形，剩余部分折合起来可以制作一个有盖的正方体纸盒．（纸板厚度及接缝处忽略不计）
【问题解决：】现有一块长为、宽为的长方形纸板，请探究；
(1)、若 ， 按图1的方式剪去的小正方形边长为 ， 做成一个无盖的正方体纸盒，此时，你发现c与b之间存在的数量关系为____________．(2)、若 ， 按如图2方式裁剪，做成一个有盖的正方体纸盒，发现a与b之间存在的数量关系是________．(3)、在（2）的条件下，若 ， 求有盖正方体纸盒的表面积．