截一个几何体—北师大版数学七(上)知识点训练
试卷更新日期:2024-10-15 类型:复习试卷
一、基础夯实
-
1. 用一个平面去截下列几何体,截面一定是圆的是( )A、
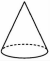 B、
B、 C、
C、 D、
D、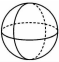 2. 如图,用一个平面去截一个圆锥,截面的形状是( )
2. 如图,用一个平面去截一个圆锥,截面的形状是( )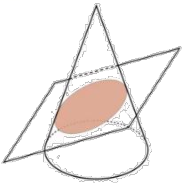 A、
A、 B、
B、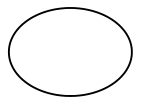 C、
C、 D、
D、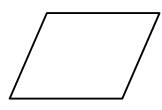 3. 一个物体的外形是长方体,其内部构造不详.用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图2所示,这个长方体的内部构造可能是( )
3. 一个物体的外形是长方体,其内部构造不详.用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图2所示,这个长方体的内部构造可能是( ) A、圆柱 B、棱柱 C、棱锥 D、圆锥4. 如图,一个密闭的圆柱形玻璃杯中装一半的水,任意放置这个玻璃杯,则水面的形状不可能是 ( )
A、圆柱 B、棱柱 C、棱锥 D、圆锥4. 如图,一个密闭的圆柱形玻璃杯中装一半的水,任意放置这个玻璃杯,则水面的形状不可能是 ( ) A、
A、 B、
B、  C、
C、  D、
D、 5. 用一个平面去截长方体,三棱柱,圆柱,和圆锥,其中不能截出三角形的几何体是.6. 用一个平面去截一个几何体,截面是圆形,这个几何体可能是请写出两个7. 用一个平面去截正方体,所得截面可能是、、、 .8. 用一个平面去截一个几何体,如果截面的形状是长方形,你能想象出原来的几何体可能是什么吗?9. 分别指出图中几何体的截面形状的标号:
5. 用一个平面去截长方体,三棱柱,圆柱,和圆锥,其中不能截出三角形的几何体是.6. 用一个平面去截一个几何体,截面是圆形,这个几何体可能是请写出两个7. 用一个平面去截正方体,所得截面可能是、、、 .8. 用一个平面去截一个几何体,如果截面的形状是长方形,你能想象出原来的几何体可能是什么吗?9. 分别指出图中几何体的截面形状的标号: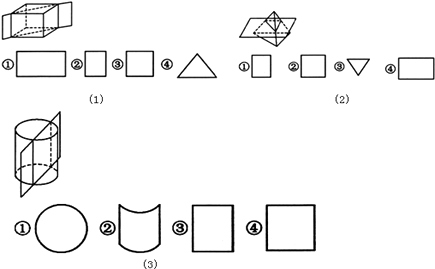 (1)、中截面形状的标号:;(2)、中截面形状的标号:;(3)、中截面形状的标号: .
(1)、中截面形状的标号:;(2)、中截面形状的标号:;(3)、中截面形状的标号: .二、能力提升
-
10. 下列几何体中截面不可能是长方形的是( )A、
 B、
B、 C、
C、 D、
D、 11. 作为中国四大传统节日之一,中秋节自古有祭月、赏月、吃月饼、玩花灯、赏桂花等民俗.如图所示,某月饼可以看成一个圆柱体,用一个平面去截该圆柱体,则截面不可能是( )
11. 作为中国四大传统节日之一,中秋节自古有祭月、赏月、吃月饼、玩花灯、赏桂花等民俗.如图所示,某月饼可以看成一个圆柱体,用一个平面去截该圆柱体,则截面不可能是( )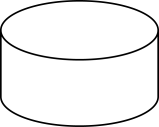 A、三角形 B、圆 C、长方形 D、正方形12. 用一个平面去截一个几何体,得到的截面是六边形,这个几何体可能是( )A、三棱锥 B、三棱柱 C、四棱锥 D、正方体13. 把一个棱长为a米的正方体、任意截成两个长方体,这两个长方体的表面积是( )A、6a2平方米 B、7a2平方米 C、8a2平方米 D、12a2平方米14. 如图,用一个平面去截一个三棱柱,截面的形状不可能是( )
A、三角形 B、圆 C、长方形 D、正方形12. 用一个平面去截一个几何体,得到的截面是六边形,这个几何体可能是( )A、三棱锥 B、三棱柱 C、四棱锥 D、正方体13. 把一个棱长为a米的正方体、任意截成两个长方体,这两个长方体的表面积是( )A、6a2平方米 B、7a2平方米 C、8a2平方米 D、12a2平方米14. 如图,用一个平面去截一个三棱柱,截面的形状不可能是( ) A、三角形 B、四边形 C、五边形 D、六边形15. 用一平面去截下列几何体,其截面可能是长方形的有( )
A、三角形 B、四边形 C、五边形 D、六边形15. 用一平面去截下列几何体,其截面可能是长方形的有( )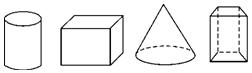 A、1个 B、2个 C、3个 D、4个16. 用一个平面去截一个几何体,截面是三角形,这个几何体不可能是( )A、棱柱 B、圆柱 C、圆锥 D、棱锥17. 用一个平面截下列几何体,截面可能是三角形的是( )
A、1个 B、2个 C、3个 D、4个16. 用一个平面去截一个几何体,截面是三角形,这个几何体不可能是( )A、棱柱 B、圆柱 C、圆锥 D、棱锥17. 用一个平面截下列几何体,截面可能是三角形的是( )①正方体②球体③圆柱④圆锥
A、① B、①② C、①④ D、①③④18. 用一个平面去截一个正方体,不可能出现哪个截面?( )A、四边形 B、五边形 C、六边形 D、七边形19. 如图,用一个平面从不同的角度去截一个正方体,则截面大小、形状相同的是( ) A、(1)(2)相同,(3)(4)相同 B、(1)(3)相同,(2)(4)相同 C、(1)(4)相同,(2)(3)相同 D、都不相同20. 如图所示,用经过A , B , C三点的平面截去正方体的一角,变成一个新的多面体,若这个多面体的面数为m , 棱数为n , 则.
A、(1)(2)相同,(3)(4)相同 B、(1)(3)相同,(2)(4)相同 C、(1)(4)相同,(2)(3)相同 D、都不相同20. 如图所示,用经过A , B , C三点的平面截去正方体的一角,变成一个新的多面体,若这个多面体的面数为m , 棱数为n , 则. 21. 把一个立方体锯掉一个角后(如图),顶点的个数是 , 面的个数是
21. 把一个立方体锯掉一个角后(如图),顶点的个数是 , 面的个数是 22.
22.如图是三个三棱柱,用一刀切下去.

(1)把图①中的三棱柱分割成两个完全相同的三棱柱;
(2)把图②中的三棱柱分割成一个四棱锥与一个三棱锥;
(3)把图③中的三棱柱分割成一个四棱柱与一个三棱柱.
三、拓展创新
-
23. 如图,由图1的正方体切去一角,分别可以得到图2-图5的几何体,请仔细观察,完成下题:
 (1)、填表:
(1)、填表:顶点数a
棱数b
面数c
图1
8
12
6
图2
图3
图4
图5
(2)、若顶点数,棱数,面数分别用a,b,c表示,请你猜测a,b,c之间满足怎样的数量关系?请直接写出你的结论.24. 如图1,大正方体上截去一个小正方体后,可得到图2的几何体. (1)、设原大正方体的表面积为S,图2中几何体的表面积为S′,那么S′与S的大小关系是( )A、S′>S B、S′=S C、S′<S D、不确定(2)、小明说:“设图1中大正方体各棱的长度之和为c,图2中几何体各棱的长度之和为c′,那么c′比c正好多出大正方体3条棱的长度.”若设大正方体的棱长为1,小正方体的棱长为x,请问x为何值时,小明的说法才正确?(3)、如果截去的小正方体的棱长为大正方体棱长的一半,那么图3是图2中几何体的表面展开图吗?如有错误,请在图3中修正.25. 找规律填空.(1)、一个正方体,用刀截去一个角后,所得的几何体有 个顶点.(2)、下列各图中每个正方体的棱长都是a厘米.各图的表面积分别是多少?(按图形顺序依次将答案填在对应的横线内)
(1)、设原大正方体的表面积为S,图2中几何体的表面积为S′,那么S′与S的大小关系是( )A、S′>S B、S′=S C、S′<S D、不确定(2)、小明说:“设图1中大正方体各棱的长度之和为c,图2中几何体各棱的长度之和为c′,那么c′比c正好多出大正方体3条棱的长度.”若设大正方体的棱长为1,小正方体的棱长为x,请问x为何值时,小明的说法才正确?(3)、如果截去的小正方体的棱长为大正方体棱长的一半,那么图3是图2中几何体的表面展开图吗?如有错误,请在图3中修正.25. 找规律填空.(1)、一个正方体,用刀截去一个角后,所得的几何体有 个顶点.(2)、下列各图中每个正方体的棱长都是a厘米.各图的表面积分别是多少?(按图形顺序依次将答案填在对应的横线内)
① 平方厘米;②平方厘米;③平方厘米;④平方厘米.
(3)、观察下面的几个算式:1+2+1=4;
1+2+3+2+1=9;
1+2+3+4+3+2+1=16;
1+2+3+4+5+4+3+2+1=25;
…
根据你所发现的规律,直接写出下面式子的结果:
1+2+3+…+99+100+99+…+3+2+1= .
