几何图形的初步认识—人教版数学七（上）知识点训练
试卷更新日期：2024-10-15 类型：复习试卷
一、基础夯实
-
1. 下列实物图中，能抽象出圆柱体的是（ ）A、
B、
C、
D、
2. 将下列平面图形绕轴旋转一周，可以得到图中所示的立体图形的是 ( ).
A、
B、
C、
D、
3. 如图， 是直角三角形 的高，将直角三角形 按以下方式旋转一周可以得到右侧几何体的是（ ）．
A、绕着 旋转 B、绕着 旋转 C、绕着 旋转 D、绕着 旋转4. 下列几何体是柱体的有（ ）
A、2个 B、3个 C、4个 D、5个5. 如图，某个几何体被遮住了一部分，这个几何体可能是（ ）
A、圆锥 B、圆柱 C、球 D、长方体6. 将一个直角三角形绕它的一条直角边所在直线旋转一周得到的几何体是.7. 飞机表演的“飞机拉线”用数学知识解释为 ， 三角板绕它的一条直角边旋转一周，形成一个圆锥体，这说明了 ．8.观察如图所示的直四棱柱．
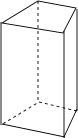(1)、它有几个面？几个底面？底面与侧面分别是什么图形？(2)、侧面的个数与底面多边形的边数有什么关系？(3)、若底面的周长为20cm ， 侧棱长为8cm ， 则它的侧面积为多少？9. 写出下图中各个几何体的名称，并按锥体和柱体把它们分类．
二、能力提升
-
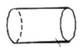
10. 用一个平面截一个几何体，得到的截面是四边形，则这个几何体可能是（ ）.A、球体 B、圆柱 C、圆锥 D、三棱锥11. 五棱柱的顶点总个数有（ ）个．A、.5 B、10 C、15 D、2012. 一个密封的圆柱体容器中装了一半的水，如果将该容器水平放置如图，那么稳定后的水面形状为（ ）
A、
B、
C、
D、
13. 按组成面的平或曲划分，与圆柱为同一类的几何体是（ ）A、长方体 B、正方体 C、棱柱 D、圆锥14. 下列说法中，正确的是（ ）A、棱柱的侧面可以是三角形 B、由六个大小一样的正方形所组成的图形是正方体的展开图 C、正方体的各条棱都相等 D、棱柱的各条棱都相等15.如图所示，该图案中有 个正方形．
16. 一个直角三角形的三条边长分别是、、 ， 若以斜边为轴旋转一周形成的图形体积是立方厘米．（π取3.14）17. 如图，某银行大堂的旋转门内部由三块宽为、高为的玻璃隔板组成．
(1)、将此旋转门旋转一周，能形成的几何体是 ， 这能说明的事实是（选择正确的一项填入）．A．点动成线 B．线动成面 C．面动成体
(2)、求该旋转门旋转一周形成的几何体的体积．（边框及衔接处忽略不计，结果保留）18. 一个长方体的长、宽、高之比为 ， 若长方体的棱长总和等于正方体的棱长总和，则长方体的表面积与正方体的表面积之比为 ， 长方体的体积与正方体的体积之比为 ．19. 将如图所示的长方体用过的平面切割，得到的两个几何体是 ．
20. 推导猜测
(1)、三棱锥有条棱，四棱锥有条棱，五棱锥有条棱．(2)、棱锥有30条棱．(3)、一个棱锥的棱数是100，则这个棱锥是棱锥，面数是 ．21. 由27个小立方体堆成的一个大立方体如下所示，现将它的表面涂成黄色．问：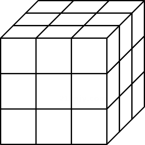
(1)、有三个面涂成黄色的小立方体有几个？(2)、有一个面涂成黄色的小立方体有几个？(3)、有两个面涂成黄色的小立方体有几个？三、拓展创新
-
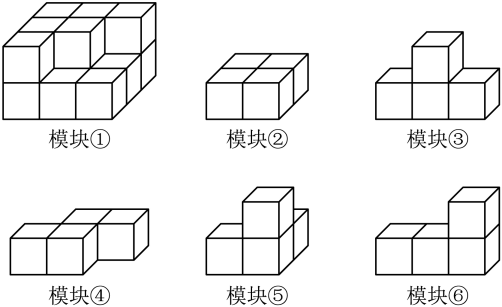
22. 如图，模块①由15个棱长为1的小正方体构成，模块②一⑥均由4个棱长为1的小正方体构成，现在从模块②一⑥中选出三个模块放到模块①上，与模块①组成一个棱长为3的大正方体，则符合上述要求的三个模块序号是 ．
23. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式，请你观察下列几种简单多面体模型，解答下列问题：
(1)、根据上面多面体模型，完成表格中的空格；多面体
顶点数（V）
面数（F）
棱数（E）
正四面体
4
①
6
长方体
8
6
②
正八面体
③
8
12
正十二面体
④
12
30
(2)、你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是；(3)、一个多面体的面数比顶点数小12，且有42条棱，则这个多面体的顶点数是 ．