立体图形—北师大版数学七(上)知识点训练
试卷更新日期:2024-10-14 类型:复习试卷
一、基础夯实
-
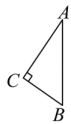
1. 将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )
 A、
A、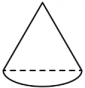 B、
B、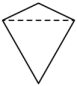 C、
C、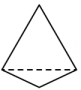 D、
D、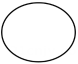 2. 下面现象说明“线动成面”的是( )A、旋转一扇门,门在空中运动的痕迹 B、扔一块小石子,石子在空中飞行的路线 C、天空划过一道流星 D、汽车雨刷在挡风玻璃上面画出的痕迹3. 在朱自清的《春》中描写春雨“像牛毛,像花针、像细丝,密密麻麻地斜织着”的语句,这说明了( )A、点动成线 B、线动成面 C、面动成体 D、两点确定一条直线4. 下列标注的图形名称与图形不相符的是( )A、
2. 下面现象说明“线动成面”的是( )A、旋转一扇门,门在空中运动的痕迹 B、扔一块小石子,石子在空中飞行的路线 C、天空划过一道流星 D、汽车雨刷在挡风玻璃上面画出的痕迹3. 在朱自清的《春》中描写春雨“像牛毛,像花针、像细丝,密密麻麻地斜织着”的语句,这说明了( )A、点动成线 B、线动成面 C、面动成体 D、两点确定一条直线4. 下列标注的图形名称与图形不相符的是( )A、 四棱锥
B、
四棱锥
B、 圆柱
C、
圆柱
C、 正方体
D、
正方体
D、 三棱锥
5.
三棱锥
5.如图,一个长方形绕轴l旋转一周得到的立体图形是( )
 A、棱锥 B、圆锥 C、圆柱 D、球6. 下列几何图形中,属于圆锥的是( )A、
A、棱锥 B、圆锥 C、圆柱 D、球6. 下列几何图形中,属于圆锥的是( )A、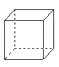 B、
B、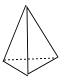 C、
C、 D、
D、 7. 对如图所示的几何体认识正确的是( )
7. 对如图所示的几何体认识正确的是( ) A、几何体是四棱柱 B、棱柱的侧面是三角形 C、棱柱的底面是四边形 D、棱柱的底面是三角形8. 三棱柱的顶点个数是( )A、3 B、4 C、5 D、69. 如图是一个几何体,请你描述这个几何体的特点(写出三点) .
A、几何体是四棱柱 B、棱柱的侧面是三角形 C、棱柱的底面是四边形 D、棱柱的底面是三角形8. 三棱柱的顶点个数是( )A、3 B、4 C、5 D、69. 如图是一个几何体,请你描述这个几何体的特点(写出三点) . 10. 一个棱柱有10个面,则这个棱柱的底面是边形.11. 如图,直角三角形绕其一条直角边旋转一周得到的几何体是 .
10. 一个棱柱有10个面,则这个棱柱的底面是边形.11. 如图,直角三角形绕其一条直角边旋转一周得到的几何体是 . 12. 六棱柱有个顶点.13.
12. 六棱柱有个顶点.13.一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考:
(1)以长方形的一边为轴把长方形绕轴旋转﹣周得到的立体图形是什么?你能画出示意图吗?
(2)把直角三角形以直角边为旋转轴旋转一周得到的几何体又是什么?以斜边呢?你能画出示意图吗?
(3)知果把图绕虚线旋转一周所得的图形是怎样的呢?你能画出示意图吗?
 14. 将下列几何体进行分类.
14. 将下列几何体进行分类. 15. 学校为实验教室配备了一只无盖的圆柱形铁皮消防桶.做这只消防桶至少需要铁皮多少平方分米?
15. 学校为实验教室配备了一只无盖的圆柱形铁皮消防桶.做这只消防桶至少需要铁皮多少平方分米? 16.
16.图中的几何体是由几个面所摆成的?面与面相交成几条线?它们是直的还是曲的?
 17.
17.如图,把一个木制正方体的表面涂上颜色,然后将正方体的棱分成相等的四份,并做上标记,得到许多小正方体.问
(1)有 个小正方体;
(2)有 个小正方体只有两面涂有颜色
(3)有 个小正方体只有3面都涂了颜色.
(4)有 个小正方体6面都未涂色.

二、能力提升
-
18. 如图,把图形绕着给定的直线旋转一周后形成的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 19. “力箭一号”(ZK﹣1A)运载火箭在酒泉卫星发射中心采用“一箭六星”的方式,成功将六颗卫星送入预定轨道,首次飞行任务取得圆满成功.把卫星看成点,则卫星在预定轨道飞行留下的痕迹体现了( )A、点动成线 B、线动成面 C、面动成体 D、面面相交成线20. 下列图形经过折叠不能围成棱柱的是( )A、
19. “力箭一号”(ZK﹣1A)运载火箭在酒泉卫星发射中心采用“一箭六星”的方式,成功将六颗卫星送入预定轨道,首次飞行任务取得圆满成功.把卫星看成点,则卫星在预定轨道飞行留下的痕迹体现了( )A、点动成线 B、线动成面 C、面动成体 D、面面相交成线20. 下列图形经过折叠不能围成棱柱的是( )A、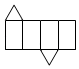 B、
B、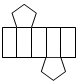 C、
C、 D、
D、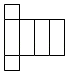 21. 下列说法中,正确的有( )
21. 下列说法中,正确的有( )①圆锥和圆柱的底面都是圆 ②棱锥底面边数与侧棱数相等
③棱柱的上下底面是形状、大小相同的多边形 ④正方体是四棱柱,四棱柱是正方体.
A、1个 B、2个 C、3个 D、4个22. 由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( ) A、10 B、11 C、12 D、1323. 下列说法不正确的是( )A、长方体是四棱柱 B、八棱柱有8个面 C、六棱柱有12个顶点 D、经过棱柱的每个顶点有3条棱24. 若一个棱柱有12个顶点,则下列说法正确的是( )A、这个棱柱是十二棱柱 B、这个棱柱有4个侧面 C、这个棱柱的底面是八边形 D、这个棱柱有6条侧棱25. 下列说法正确的是( )A、棱柱的各条棱都相等 B、有9条棱的棱柱的底面一定是三角形 C、长方体和正方体不是棱柱 D、柱体的上、下两底面可以大小不一样26. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.
A、10 B、11 C、12 D、1323. 下列说法不正确的是( )A、长方体是四棱柱 B、八棱柱有8个面 C、六棱柱有12个顶点 D、经过棱柱的每个顶点有3条棱24. 若一个棱柱有12个顶点,则下列说法正确的是( )A、这个棱柱是十二棱柱 B、这个棱柱有4个侧面 C、这个棱柱的底面是八边形 D、这个棱柱有6条侧棱25. 下列说法正确的是( )A、棱柱的各条棱都相等 B、有9条棱的棱柱的底面一定是三角形 C、长方体和正方体不是棱柱 D、柱体的上、下两底面可以大小不一样26. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.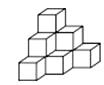 27. 用32个棱长的白色小正方体与32个棱长的蓝色小正方体拼成一个大正方体.如果使蓝色的面向外露的面积最大,那么这个大正方体的6个面上有是蓝色的.
27. 用32个棱长的白色小正方体与32个棱长的蓝色小正方体拼成一个大正方体.如果使蓝色的面向外露的面积最大,那么这个大正方体的6个面上有是蓝色的. 28. 已知一个直棱柱共有15条棱,它的底面边长都是5cm,侧棱长都是4cm,则这个棱柱的所有侧面的面积之和是 .29. 已知长方形的长为4cm、宽为3cm , 将其绕它的一边所在的直线旋转一周,得到一个几何体,
28. 已知一个直棱柱共有15条棱,它的底面边长都是5cm,侧棱长都是4cm,则这个棱柱的所有侧面的面积之和是 .29. 已知长方形的长为4cm、宽为3cm , 将其绕它的一边所在的直线旋转一周,得到一个几何体, (1)、求此几何体的表面积.(结果保留π)(2)、求此几何体的体积;(结果保留π)
(1)、求此几何体的表面积.(结果保留π)(2)、求此几何体的体积;(结果保留π)三、拓展创新
-
30. 观察下列多面体,并把表格补充完整.
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形




顶点数a
6
10
12
棱数b
9
12
面数c
5
8
(1)、完成表格中的数据;(2)、根据表格中的规律判断,十四棱柱共有 个面,共有 个顶点,共有 条棱;(3)、若某个棱柱由30个面构成,则这个棱柱为 棱柱.