数轴的点常规运动模型—人教版数学七（上）知识点训练-在线组卷题库

1. 如图，已知 $A$ ， $B (B$ 在 $A$ 的左侧 $)$ 是数轴上的两点，点 $A$ 对应的数为 $12$ ，且 $A B = 18$ ，动点 $P$ 从点 $A$ 出发，以每秒 $2$ 个单位长度的速度沿数轴向左运动，在点 $P$ 的运动过程中， $M$ ， $N$ 始终为 $A P$ ， $B P$ 的中点，设运动时间为 $t (t > 0)$ 秒，则下列结论中正确的有（）
① $B$ 对应的数是 $- 6$ ；②点 $P$ 到达点 $B$ 时， $t = 9$ ；③ $B P = 2$ 时， $t = 6$ ；
④在点 $P$ 的运动过程中，线段 $M N$ 的长度会发生变化．

A、1个 B、2个 C、3个 D、4个

查看试题解析

2. 如图，数轴上线段 $A B = 2$ （单位长度），线段 $C D = 4$ （单位长度），点A在数轴上表示的数是-12，点C在数轴上表示的数是14.若线段AB以每秒2个单位长度的速度向右匀速运动，同时线段CD以每秒1个单位长度的速度向左匀速运动.设运动时间为ts.当t=时，点B刚好与线段CD的中点重合.

查看试题解析
3. 如图，已知点A ， B ， C是数轴上三点，O为原点，点C对应的数为6， $B C = 4$ ， $A B = 12$ ，动点P ， Q分别同时从A、C出发，分别以每秒6个单位和3个单位的速度沿数轴正方向运动，M为 $A P$ 的中点，N在 $C Q$ 上，且 $C N = \frac{1}{3} C Q$ ，则经过秒时， $M N$ 之间距离为4．

查看试题解析
4. 如图，在数轴上点A、B表示的数分别为-2、4，若点M从A点出发以每秒5个单位长度的速度沿数轴向右匀速运动，点N从B点出发以每秒3个单位长度的速度沿数轴匀速运动，设点M、N同时出发，经过秒后，M、N两点间的距离为10个单位长度．

查看试题解析

5. 如图，已知数轴上点A表示的数为－2，点B是数轴上在点A右侧的一点，且A、B两点间的距离为4．动点Р从点A出发，以每秒3个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒.

(1)、数轴上点B表示的数是，点Р表示的数是（用含t的代数式表示）；

(2)、动点Q从点B出发，以每秒5个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，求：
①当点Р运动多少秒时，点P与点Q重合?
②当点Р运动多少秒时，点P与点Q之间的距离为3个单位长度?（②直接写出t的值）.

查看试题解析
6. 如图，数轴上点A表示数a，点B表示数b，且a、b满足 $| a + 4 | + {(b - 14)}^{2} = 0$ ．

(1)、点A表示的数为；点B表示的数为；

(2)、若数轴上有两动点P，Q，点P以4个单位/秒从A向右运动，同时点Q以2个单位/秒从点B向左运动，问经过几秒P，Q相遇？

(3)、在（2）的条件下，动点P、Q出发经过多少秒，能使 $P A = 3 Q O$ ？

查看试题解析
7. 对于数轴上的A，B，C三点，给出如下定义：若其中一个点与其它两个点的距离恰好满足2倍的数量关系，则称该点是其它两个点的“联盟点”．例如：数轴上点A，B，C所表示的数分别为1，3，4，此时点B是点A，C的“联盟点”．

(1)、若点A表示数 $- 1$ ，点B表示的数2，下列各数： $- \frac{2}{3}$ ， 0，1，4，5所对应的点分别为 $C_{1} ， C_{2} ， C_{3} ， C_{4} ， C_{5}$ ，其中是点A，B的“联盟点”的是；

(2)、点A表示的数是 $- 1$ ，点B表示的数是3，P是数轴上的一个动点：
①若点P在线段 $A B$ 上，且点P是点A，B的“联盟点”，求此时点P表示的数：
②若点P在点A的左侧，点P、A、B中有一个点恰好是其它两个点的“联盟点”，求出此时点P表示的数．

查看试题解析
8. 已知数轴上两点 $A$ ， $B$ 对应的数分别为 $- 10$ ， 2，点 $M$ 为数轴上任意一点，其对应的数为 $x$ ．

(1)、 $A B$ 的长为．

(2)、数轴上是否存在点 $M$ ，使点 $M$ 到点 $A$ ，点 $B$ 的距离之和是18？若存在，求出 $x$ 的值；若不存在，请说明理由．

(3)、如果点 $P$ 以每秒1个单位长度的速度从点 $A$ 出发沿数轴向右运动，同时点 $Q$ 从点 $B$ 出发以每秒2个单位长度的速度沿数轴向左运动，当点 $Q$ 到达点 $A$ 时，点 $P$ 与 $Q$ 同时停止运动，设点 $P$ 的运动时间为 $t$ 秒（ $t > 0$ ）．
①求出点 $P$ 与点 $Q$ 相遇时 $t$ 的值；
②当点 $P$ ，点 $Q$ 与点 $A$ 三个点中，其中一个点是另两个点构成线段的中点时，直接写出 $t$ 的值．

查看试题解析

9. 【阅读理解】数轴体现了“数形结合”的数学思想，能帮助我们直观分析问题．若数轴上点A，B表示的数分别为a，b，A、B两点之间的距离可表示为AB＝|a-b|．如：点A表示的数为2，点B表示的数为5，则AB=|2-5|=3.

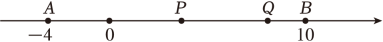(1)、【问题提出】填空：如图，数轴上点A表示的数为-4，点B表示的数为10，AB=；

(2)、【拓展探究】著点P从点A出发，以每秒4个单位长度的速度沿数轴向右运动，同时点Q从点B出发，以每秒3个单位长度的速度沿数轴向左运动，设运动时间为t妙：
①用含t的式子表示：t秒后，点P表示的数为 ▲ ，点Q表示的数为 ▲ ．
②求当t为何值时，P，Q两点相遇，并写出相遇点所表示的数．

查看试题解析

10. 甲、乙两人借助“数轴”和“剪刀、石头、布”设计了一款“移动游戏”

.

两人分别在数轴上随机挑选一个点作为游戏的起点：甲选择的游戏起点记为

A

，乙选择的游戏起点记为

B

；然后两人进行“剪刀、石头、布”，每次“剪刀、石头、布”的结果共有三种可能：平局、甲胜、乙胜；再根据每次“剪刀、石头、布”的结果，

A

、

B

两点沿数轴同时移动，移动规则如下：

“剪刀、石头、布”的结果	A、 $B$ 两点移动方式
平局	点 $A$ 向右移动 $0.5$ 个单位，点 $B$ 向左移动 $0.5$ 个单位
甲胜	点 $A$ 向右移动 $2$ 个单位，点 $B$ 向右移动 $1$ 个单位
乙胜	点 $A$ 向左移动 $1$ 个单位，点 $B$ 向左移动 $2$ 个单位

设甲、乙两人共进行了 $k$ 次“剪刀、石头、布” $(k$ 为正整数 $)$ ．

(1)、如图，起点

A

表示的数是

- 5

，起点

B

表示的数是

3

．

$①$ 当 $k = 3$ 时，其中平局一次，甲胜一次，点 $A$ 最终位置表示的数为，点 $B$ 最终位置表示的数为，此时 $A$ 、 $B$ 两点间的距离为．

$②$ 当 $k = 10$ 时，其中平局 $x$ 次，甲胜 $y$ 次，求 $A$ 、 $B$ 两点最终位置表示的数 $. ($ 用含 $x$ 、 $y$ 的代数式表示 $)$

(2)、若起点

A

表示的数是

a

，起点

B

表示的数是

b (a

、

b

均为整数，且

a < b)

，当

A

、

B

两点最终位置相距

3

个单位时，探究

k

的值，直接写出结论

. (

用含

a

、

b

的代数式表示

)

查看试题解析

11. 阅读下列材料：
我们给出如下定义：数轴上给定不重合两点A，B，若数轴上存在点M，使得点M到点A的距离等于点M到点B的距离的2倍，则称点M为点A与点B的“亚运点”．其中在A，B之间的点M为点A与点B的“亚运@未来点”
解答下列问题：

(1)、若点A表示的数为-5，点B表示的数为1，点M为点A与点B的“亚运点”，则点M表示的数为；

(2)、若A、B两点的“亚运点”M表示的数为2，且A、B两点的距离为9（A在B的左侧），则点A表示的数为，

(3)、点A表示的数为-6，点C，D表示的数分别是-2，0，点O为数轴原点（与静止时的D点重合），点B为线段CD上一点（点B可以与点C与点D重合）．
①设点M表示的数为m，若点M可以为点A与点B的“亚运@未来点”，则m可取得整数有；
②若点A和点D同时以每秒2个单位长度的速度向数轴正半轴方向移动．设移动的时间为t（t＞0）秒，求t的所有整数值，使得点O可以为点A与点B的“亚运@未来点”．

查看试题解析
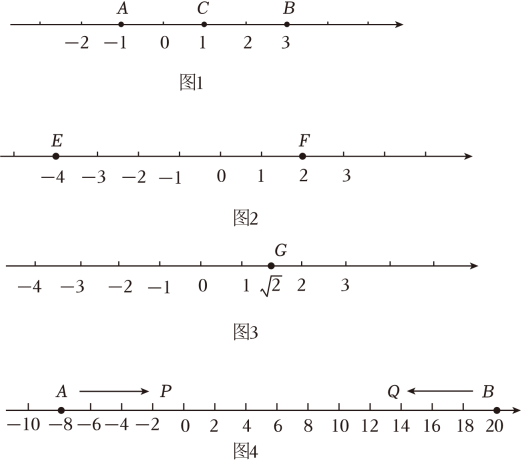
12. 新定义学习：
【新知学习】若A，B，C是数轴上的三个点，如果点C到A的距离等于点C到B的距离，那么我们就称点C是AB的中点．例如，如图1，点A表示的数为-1，点B表示的数为3，表示数1的点C到点A的距离是2，到点B的距离是2，那么点C是AB的中点．

(1)、【知识运用】
①如图2，E、F为数轴上两点，点E所表示的数为-4，点F所表示的数为2，求EF的中点所表示的数，并说明理由．
②如图3，若数 $\sqrt{2}$ 所表示的点G是MN的中点，那么M表示的数为， N表示的数为（只要写出符合条件的一对值即可）．

(2)、【知识拓展】如图4，A，B为数轴上两点，点A所表示的数为-8，点B所表示的数为20．现有一只电子蜗牛P从点A出发，以1个单位每秒的速度向右运动；同时另一只电子蜗牛Q从点B出发，以2个单位每秒的速度向左运动，若点M，N分别是AP和BQ的中点，则在P，Q的运动过程中，当t＝秒时，M，N点到原点的距离相等（请直接写出答案）．

查看试题解析

数轴的点常规运动模型—人教版数学七（上）知识点训练

一、选择题

二、填空题

三、解答题

四、实践探究题