数轴上的和差倍分—北师大版数学七（上）知识点训练

试卷更新日期：2024-10-14 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，O，A，B，C四点在数轴上，其中O为原点，且AC=2，OA=2OB，若C点所表示的数为m，则B点所表示的数正确的是（）

A、-2（m+2） B、 $\frac{m - 2}{2}$ C、 $\frac{m + 2}{2}$ D、 $\frac{2 - m}{2}$

查看试题解析
2. 已知 $A$ ， $B$ 为数轴上的两点， $A$ ， $B$ 所对应的数分别是-5和4， $P$ 为线段 $A B$ 的三等分点( $P$ 点靠近 $A$ 点)，则 $P$ 点所对应的数是（）

A、 $- 2$ B、 $- 1$ C、 $- \frac{1}{2}$ D、 $1$

查看试题解析
3. 如图，数轴上有A，B，C，D四个整数点（即各点均表示整数），且2AB=BC=3CD.若A，D两点所表示的数分别是﹣5和6，则线段BD的中点所表示的数是（）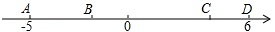

A、6 B、5 C、3 D、2

查看试题解析
4. 已知在数轴上，点A表示的数为x₁ ，点B表示的数为x₂ ，点O表示的数为0，且x_l ＜0＜ x₂ ， $| x_{2} | = 2 | x_{1} |$ ，则（）

A、AO＋ $\frac{1}{2}$ AB＝2BO B、BO＝ $\frac{1}{2}$ AB C、2AO＋ $\frac{1}{2}$ BO ＝AB D、BO＝ $\frac{1}{3}$ AB

查看试题解析
5. 如图，数轴上四点 $O$ ， $A$ ， $B$ ， $C$ ，其中 $O$ 为原点，且 $A C = 3$ ， $O A = O B$ ，若点 $C$ 表示的数为 $x$ ，则点 $B$ 表示的数为（）

A、 $- (x + 3)$ B、 $- (x - 3)$ C、 $x + 3$ D、 $x - 3$

查看试题解析
6. 已知数轴上点A，B，C所表示的数分别是4，x，10，其中点B为AC的三等分点，则x的值是。

查看试题解析
7. 已知 $A$ ， $B$ ， $C$ 是数轴上的三个点，且 $C$ 在 $B$ 的右侧.点 $A$ 、 $B$ 表示的数分别是 $1$ 、 $3$ ，若 $B C = 2 A B$ ，则点 $C$ 表示的数是.

查看试题解析
8.
如图，已知数轴上A、B两点所表示的数分别为﹣2和8．
（1）求线段AB的长；

（2）若P为射线BA上的一点（点P不与A、B两点重合，M为PA的中点，N为PB的中点，当点P在射线BA上运动时；MN的长度是否发生改变？若不变，请你画出图形，并求出线段MN的长；若改变，请说明理由．

查看试题解析

二、能力提升

9. 在数轴上，点M、N分别表示数m，n. 则点M，N 之间的距离为|m-n|.已知点A，B，C，D在数轴上分别表示的数为a，b，c，d.且|a-c|=|b-c|= $\frac{2}{5}$ |d-a|=1 (a≠b)，则线段BD的长度为（）

A、3.5 B、0.5 C、3.5或0.5 D、4.5或0.5

查看试题解析
10. 如图，点A，P，Q，B在一条不完整的数轴上，点A表示数-3，点B表示数3，若动点P从点A出发以每秒1个单位长度向终点B匀速运动，同时动点Q从点B出发以每秒2个单位长度向终点A匀速运动，其中一点到达终点时，另一个点也随之停止运动，当BP=3AQ时，点P在数轴上表示的数是（）

A、2.4 B、-1.8 C、0.6 D、-0.6

查看试题解析
11. 已知多项式 $x^{2} - 3 x y^{2} - 4$ 的常数项是a，次数是b，且a，b两个数轴上所对应的点分别为A、B，若点A、点B同时沿数轴向正方向运动，点A的速度是点B的2倍，且3秒后， $\frac{3}{2} O A = O B$ ，求点B的速度为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{4}$ 或 $\frac{3}{4}$ C、 $\frac{1}{4}$ 或 $\frac{3}{2}$ D、 $\frac{3}{2}$

查看试题解析
12. 数轴上，点 $A$ 对应的数是 $- 6$ ，点 $B$ 对应的数是 $- 2$ ，点 $O$ 对应的数是0.动点 $P$ 、 $Q$ 从 $A$ 、 $B$ 同时出发，分别以每秒3个单位和每秒1个单位的速度向右运动.在运动过程中，下列数量关系一定成立的是（）

A、 $P Q = 2 O Q$ B、 $O P = 2 P Q$ C、 $3 Q B = 2 P Q$ D、 $P B = P Q$

查看试题解析
13. 在数轴上，点A，O，B分别表示－16，0，14，点P，Q分别从点A，B同时开始沿数轴正方向运动，点P的速度是每秒3个单位，点Q的速度是每秒1个单位，运动时间为t秒．若点P，Q，O三点在运动过程中，其中一点恰好是另外两点为端点构成的线段的三等分点时，则运动时间为秒.

查看试题解析
14. 如图，在数轴上，点A，B分别表示-15，9，点P，Q分别从点A，B同时开始沿数轴正方向运动，点P的速度是每秒3个单位，点Q的速度是每秒1个单位，运动时间为t秒．在运动过程中，当点P，点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点时，t的值是．

查看试题解析
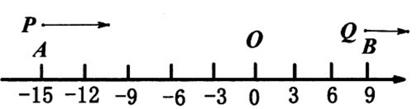15. 如图，点O是数轴的原点，点A在数轴上位于原点左侧，点B在数轴上位于原点右侧， $A B = m$ ．

(1)、当 $A B = m$ ， $A B = 4 O B$ 时，点A表示的数为，点B表示的数为；

(2)、若点C、D为数轴上任意两点，点M是线段AC的中点，点N是线段BD的中点．
①当点C与点D重合时，探究AB与MN的数量关系，并说明理由．
②当 $C D = n$ 时，直接写出MN的长度（用m ， n表示）．

查看试题解析
16. 数轴是数学中的一个重要工具，利用数轴可以将数与形进行完美的结合，如：数轴上点 $A$ 表示的数为 $a$ ，点 $B$ 表示的数为 $b$ ，则 $A ， B$ 两点之间的距离为 $A B = | a - b |$ ．如图所示，点 $A ， B ， C$ 为数轴上的三个点，表示的数分别为 $a ， b ， c$ ，满足 ${(a + 12)}^{2} + | b + c | = 0$ ，且 $b$ 为 $- \frac{1}{3}$ 的倒数．动点 $M$ ， $P$ 分别从点 $A ， B$ 出发，分别以每秒1个单位长度和4个单位长度的速度向右运动，动点 $N$ 从点 $C$ 出发，以每秒3个单位长度的速度向左运动，三个动点同时出发，设运动的时间为 $t$ 秒（ $t > 0$ ），请回答下列问题：

(1)、直接写出 $a ， b ， c$ 的值： $a =$ ， $b =$ ， $c =$ ；

(2)、当 $M N = 3$ 时，求 $t$ 的值；

(3)、在运动过程中， $P M - C N$ 的值是否发生变化？若发生变化，请用含 $t$ 的式子表示；若不发生变化，请求出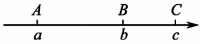 $P M - C N$ 的值．

查看试题解析
17. 如图：在数轴上A点表示数a，B点表示数b，C点表示数c，b是最小的正整数，且a，c满足|a+2|+（c-7）²＝0.

(1)、a＝， b＝， c＝；

(2)、若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合；

(3)、点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，则AB＝， AC＝， BC＝.（用含t的代数式表示）

(4)、请问：3BC-2AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值.

查看试题解析

三、拓展创新

18. 已知数轴上两点A、B，若在数轴上存在一点C，使得 $A C + B C = n A B$ ，则称点C为线段AB的“n倍点”.例如图1所示：当点A表示的数为－2，点B表示的数为2，点C表示的数为0，有 $A C + B C = 2 + 2 = 4 = A B$ ，则称点C为线段AB的“1倍点”.

图1 图2

备用图备用图
请根据上述规定回答下列问题：
已知图2中，点A表示的数为－3，点B表示的数为1，点C表示的数为x.

(1)、当 $- 3 \leq x \leq 1$ 时，点C（填“一定是”或“一定不是”或“不一定是”）线段AB的“1倍点”；

(2)、若点C为线段AB的“n倍点”，且 $x = - 4$ ，求n的值；

(3)、若点D是线段AB的“2倍点”，则点D表示的数是多少？请说明理由.

查看试题解析