数轴上的和差倍分—人教版数学七（上）知识点训练

试卷更新日期：2024-10-14 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，在数轴上，点A、B表示的数分别是 $- 19$ 和3．点C为线段 $A D$ 的中点，且 $B C = 6 B D$ ，则点C表示的数为（）．

A、 $- 9$ B、 $- 9.5$ C、 $- 10$ D、 $- 10.5$

查看试题解析
2. 如图，未标出原点的数轴上有A，B，C，D，E，F六个点，若相邻两点之间的距离相等，则点D所表示的数是（）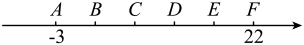

A、15 B、12 C、11 D、10

查看试题解析
3. 在数轴上有六个点，且 $A B = B C = C D = D E = E F$ ，则点 $C$ 所表示的数最接近的整数是（）

A、2 B、1 C、0 D、 $- 1$

查看试题解析
4. 数轴上，点A对应的数是﹣6，点B对应的数是﹣2，点O对应的数是0.动点P、Q从A、B同时出发，分别以每秒3个单位和每秒1个单位的速度向右运动.在运动过程中，下列数量关系一定成立的是（　　）

A、PQ＝2OQ B、OP＝2PQ C、3QB＝2PQ D、PB＝PQ

查看试题解析
5. 如图，数轴上四点 $O$ ， $A$ ， $B$ ， $C$ ，其中 $O$ 为原点，且 $A C = 3$ ， $O A = O B$ ，若点 $C$ 表示的数为 $x$ ，则点 $B$ 表示的数为（）

A、 $- (x + 3)$ B、 $- (x - 3)$ C、 $x + 3$ D、 $x - 3$

查看试题解析
6. 已知在数轴上，点A表示的数为x₁ ，点B表示的数为x₂ ，点O表示的数为0，且x_l ＜0＜ x₂ ， $| x_{2} | = 2 | x_{1} |$ ，则（）

A、AO＋ $\frac{1}{2}$ AB＝2BO B、BO＝ $\frac{1}{2}$ AB C、2AO＋ $\frac{1}{2}$ BO ＝AB D、BO＝ $\frac{1}{3}$ AB

查看试题解析
7. 如图，在数轴上有A，B，C，D四个点，且2AB=BC=3CD，若A，D两点表示的数分别为-5，6，点E为BD的中点，则该数轴上点E表示的数是.

查看试题解析
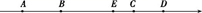8. 如图，数轴上A、B两点所表示的数分别是－4和2，点C是线段AB的中点，则点C所表示的数是.

查看试题解析
9. 已知数轴上有点A，B，C，它们所表示的数分别是+4，-6，x(x<0)．

(1)、求线段AB的长．

(2)、求线段AB的中点D所表示的数．

(3)、若AC=8，求x的值．

(4)、求线段OD(O为原点)的长．

查看试题解析
10. 如图，数轴上点A，B，M，N表示的数分别为－1，5，m，n，且AM＝ $\frac{2}{3}$ AB，点N是线段BM的中点，求m，n的值．

查看试题解析

二、能力提升

11. 在数轴上，点M、N分别表示数m，n.则点M、N之间的距离为 $| m - n |$ .已知点A，B，C，D在数轴上分别表示的数为a，b，c，d.且 $| a - c | = | b - c | = 2 ， \frac{2}{5} | d - a | = 1 (a \neq b)$ ，则线段 $B D$ 的长度为（）

A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.5

查看试题解析
12. 在数轴上，点 $A$ 对应的数为 $a$ ，点 $B$ 对应的数为 $b$ ，且 $a$ ， $b$ 满足 $| a + 5 | + {(b - 3)}^{2} = 0$ ．点 $P$ 为直线 $A B$ 上点 $B$ 右边的一点，且 $A P = 3 P B$ ，点 $Q$ 为 $P B$ 中点，则线段 $A Q$ 的长为（）

A、6 B、8 C、10 D、15

查看试题解析
13. 如图，数轴上的点 $O$ 和点 $A$ 分别表示0和10，点 $P$ 是线段 $O A$ 上一动点.点 $P$ 沿 $O \to A \to O$ 以每秒2个单位的速度往返运动1次， $B$ 是线段 $O A$ 的中点，设点 $P$ 运动时间为 $t$ 秒（ $t$ 不超过10秒）.若点 $P$ 在运动过程中，当 $P B = 2$ 时，则运动时间 $t$ 的值为（）

A、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒 B、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 或 $\frac{17}{2}$ 秒 C、3秒或7秒 D、3秒或 $\frac{13}{2}$ 或7秒或 $\frac{17}{2}$ 秒

查看试题解析
14. 数轴上，点 $A$ 对应的数是 $- 6$ ，点 $B$ 对应的数是 $- 2$ ，点 $O$ 对应的数是0.动点 $P$ 、 $Q$ 从 $A$ 、 $B$ 同时出发，分别以每秒3个单位和每秒1个单位的速度向右运动.在运动过程中，下列数量关系一定成立的是（）

A、 $P Q = 2 O Q$ B、 $O P = 2 P Q$ C、 $3 Q B = 2 P Q$ D、 $P B = P Q$

查看试题解析
15. 如图，一条数轴上点A表示-12，点B表示10，点C表示20．动点P从点A出发，以2个单位/秒的速度沿着数轴的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1个单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．

(1)、当t=秒时，点P运动到O点.

(2)、当t=秒时，PO=2QB.

查看试题解析
16. 数轴上的点A，C，B分别表示-2，4，8，若 $A C = B D$ ，则数轴上的点D表示的数是．

查看试题解析
17. 数轴上A，B两点表示的数分别为-4，2，C是射线BA上的一个动点，以C为折点，将数轴向左对折，点B的对应点落在数轴上的B'处.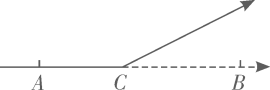

(1)、当点C是线段AB的中点时，线段AC=.

(2)、若B'C=3AC，则点C表示的数是.

查看试题解析
18. 如图，在数轴上 $A$ 点表示数a，B点表示数 $b$ ，且a、b满足 $| a + 12 | + (b - 6)^{2} = 0$ .

(1)、求A、B两点之间的距离；

(2)、点C、D在线段AB上，AC为14个单位长度，BD为8个单位长度，求线段CD的长；

(3)、在（2）的条件下，动点P以3个单位长度/秒的速度从A点出发沿正方向运动，同时点 $Q$ 以2个单位长度/秒的速度从 $D$ 点出发沿正方向运动，求经过几秒，点 $P$ 、点 $Q$ 到点 $C$ 的距离相等.

查看试题解析
19. 点O为数轴的原点，点A，B在数轴上的位置如图所示，点A表示的数为5，线段AB的长为线段OA长的1.2倍，点C在数轴上．

(1)、点B表示的数为；

(2)、若线段BC＝5，求线段OC的长；

(3)、在（2）的条件下，若点M为线段OC的中点，直接写出线段AM的长．

查看试题解析

三、拓展创新

20. 如图①，点C在线段AB上，图中有三条线段AB、AC和BC ，在这三条线段中，若其中一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”，如图②，点A和B在数轴上表示的数分别是﹣10和26，点C是线段AB的巧点，则点C在数轴上表示的数为．

查看试题解析
21. 长方形纸片上有一数轴，剪下6个单位长度(从-1到5)的一条线段，并把这条线段沿某点折叠，然后在重叠部分某处剪一刀得到三条线段(如图所示)．若这三条线段的长度之比为1：1：2，则折痕处对应的点所表示的数可能是．

查看试题解析
22. 阅读理解：
若A ， B ， C为数轴上三点且点C在A ， B之间，若点C到A的距离是点C到B的距离的3倍，我们就称点C是（A ， B）的好点．

例如，如图1，点A表示的数为－2，点B表示的数为2．表示1的点C到A的距离是3，到B的距离是1，那么点C是（A ， B）的好点；又如，表示－1的点D到A的距离是1，到B的距离是3，那么点D就不是（A ， B）的好点，但点D是（B ， A）的好点．

知识运用：

(1)、若M、N为数轴上两点，点M所表示的数为－6，点N所表示的数为2．
数所表示的点是（M ， N）的好点；

数所表示的点是（N ， M）的好点；

(2)、若点A表示的数为a ，点B表示的数为b ，点B在点A的右边，且点B在A ， C之间，点B是（C ， A）的好点，求点C所表示的数（用含a、b的代数式表示）；

(3)、若A、B为数轴上两点，点A所表示的数为－33，点B所表示的数为27，现有一只电子蚂蚁P从点A出发，以每秒6个单位的速度向右运动，运动时间为t秒．如果P ， A ， B中恰有一个点为其余两点的好点，求t的值．

查看试题解析