判断数轴上未知数的数量关系—人教版数学七（上）知识点训练

试卷更新日期：2024-10-14 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，数轴上的点A、B分别对应实数a、b，下列结论中正确的是（）

A、 $a + b < 0$ B、 $- a + b < 0$ C、 $a - b < 0$ D、 $- a - b > 0$

查看试题解析
2. 实数a在数轴上的对应点的位置如图所示.若实数b满足-a<b<a，则b的值可以是( )

A、2 B、-1 C、-2 D、-3

查看试题解析
3. 如图，数轴上点A、B、C、D所表示的数分别是a、b、c、d，若abcd＜0，ab＞cd，则原点的位置在（）

A、点A的左边 B、线段AB上 C、线段BC上 D、线段CD上

查看试题解析
4. 实数 $a$ 、 $b$ 、 $c$ 在数轴上对应点的位置如图所示，以下结论正确的是（）

A、 $a c < 0$ B、 $| a + b | = a - b$ C、 $| c - a | = a - c$ D、 $| a | > | b |$

查看试题解析
5. 若a、b为有理数，它们在数轴上的位置如图所示，那么a、b、﹣a、﹣b的大小关系是（）

A、b＜﹣a＜﹣b＜a B、b＜﹣b＜﹣a＜a C、b＜﹣a＜a＜﹣b D、﹣a＜﹣b＜b＜a

查看试题解析
6. 实数a，b在数轴上的对应点如图所示，则下列结论中① $a < b$ ；② $a + b < 0$ ；③ $a - b < 0$ ；④ $a b > 0$ ， ⑤ $\frac{a}{b} < 0$ 其中正确的有．（填序号）

查看试题解析
7. 已知 $a ， b ， c$ 三个有理数在数轴上的位置如图所示．

(1)、 $a + b$ 0， $a b c$ 0；（填“>”或“<”）

(2)、如果 $a ， c$ 互为相反数，则 $\frac{a}{c} =$ ；

(3)、化简： $| b - c | - 3 | a - b | - | b - c |$

查看试题解析
8. 有理数a，b在数轴上的对应点的位置如图所示．

(1)、判断： $- a$ _______1（填“＞”，“＜”或“＝”）；

(2)、用“＜”将 $a$ ， $a + 1$ ， $b$ ， $- b$ 连接起来（直按写出结果）

查看试题解析

二、能力提升

9. 如图，数轴上点 A， M， B 分别表示数 $a, a + b, b$ ，若 $A M > B M$ ，则下列运算结果一定是正数的是（）

A、 $a + b$ B、 $a - b$ C、a b D、 $| a | - b$

查看试题解析
10. 有理数a，b，c在数轴上对应的点的位置如图所示，给出下面三个判断：① $a b c > 0$ ；② $a + c < 0$ ；③ $| b | < 1 - a c$ ．其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
11. 如图，在数轴上点A表示的数是 $- 1$ ，点B表示的数是b ，点P是数轴上的一点，且满足 $A P = 2 B P$ ，则点P表示的数（用含b的式子表示）是（）

A、 $\frac{b - 2}{3}$ 或 $\frac{2 b - 1}{3}$ B、 $\frac{2 b - 1}{3}$ C、 $\frac{b - 2}{3}$ D、 $\frac{2 b - 1}{3}$ 或 $2 b + 1$

查看试题解析
12. 已知实数a，b在数轴上的对应点如图所示，下列式子：① $| a | < | b |$ ；② $a b < 0$ ；③ $a + b > 0$ ；④ $\frac{| a |}{a} + \frac{b}{| b |} = 0$ ．其中正确结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
13. 已知a、b是有理数，a、b在数轴上的对应点的位置如图所示，有以下结论：① $b < 0$ ；② $b - a > 0$ ；③ $| a | > - b$ ；④ $\frac{a}{b} > - 1$ ，则所有正确结论的序号是．

查看试题解析
14. 已知有理数 $a, b$ 在数轴上的位置如图，且 $| a | = | b |$ ，则关于x的方程 $2022 (a + b) - \frac{2 a}{b} x = 10$ 的解为．

查看试题解析
15. 已知数a，b，c的大小关系如图所示：

则下列各式：① $(- a) - b + c > 0$ ；② $b + a + (- c) > 0$ ；③ $\frac{a}{| a |} + \frac{b}{| b |} + \frac{| c |}{c} = 1$ ；④ $b c - a > 0$ ；⑤ $| a - b | - | c + b |$ $+ | a - c | = - 2 b$ ，其中正确的有（请填写编号）．

查看试题解析
16. 有理数a，b在数轴上对应点的位置如图所示，给出下列关系式；① $a < 0$ ， $b > 0$ ；② $a - b > 0$ ；③ $a + b > 0$ ；④ $|a| - |b| > 0$ ， ⑤ $\frac{| a |}{a} + \frac{| b |}{b} = 0$ ．其中正确的有（填序号）．

查看试题解析
17. 如图，在数轴上有A ， B ， C ， D四点，点A表示的数是1，点B表示的数是7，点C位于点B的左侧并与点B的距离是2，点D是线段 $A C$ 的中点．

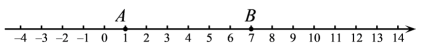(1)、在数轴上表示出点C ，点D ，直接写出点D表示的数；

(2)、若点E在数轴上，且满足 $E A = 2 E C$ ，求点E表示的数．

查看试题解析
18. 在数学综合实践活动课上，小亮借助两根小木棒 $m$ 、 $n$ 研究数学问题：如图，他把两根木棒放在数轴上，木棒的端点 $A$ 、 $B$ 、 $C$ 、 $D$ 在数轴上对应的数分别为 $a$ 、 $b$ 、 $c$ 、 $d$ ，已知 $| a + 5 | + (b + 1)^{2} = 0$ ， $c = 3$ ， $d = 8$ ．

(1)、求 $a$ 和 $b$ 的值．

(2)、小亮把木棒 $m$ 、 $n$ 同时沿 $x$ 轴正方向移动， $m$ 、 $n$ 的速度分别为 $4$ 个单位长度 $/ s$ 和 $3$ 个单位长度 $/ s$ ，设平移时间为 $t (s)$ ．
$①$ 若在平移过程中原点 $O$ 恰好是木棒 $m$ 的中点，求 $t$ 的值；
$②$ 在平移过程中，当木棒 $m$ 、 $n$ 重叠部分的长为 $3$ 个单位长度时，求 $t$ 的值．

查看试题解析

三、拓展创新

19. 【背景知识】数轴是初中数学学习的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律，例如：若数轴上点A，B分别对应数a， B．则A，B两点之间的距离为 $A B = | a - b |$ ．
【问题情境】如图，数轴上点A，B分别对应数a， B．其中 $a < 0 ， b > 0$ ．
【综合运用】

(1)、当 $a = - 8 ， b = 2$ 时，线段AB的长度是；

(2)、若该数轴上另有一点N对应着数n．
①在（1）的条件下，若点N在点A，B之间，且满足 $N A = 4 N B$ ，则数n是 ▲ ；
②当 $b = 3$ ，且 $B N = 3 A N$ 时，探究a与n之间的数量关系．

查看试题解析