有理数在数轴上的表示—人教版数学七（上）知识点训练

试卷更新日期：2024-10-14 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 数轴上，把表示 $- 4$ 的点移动1个单位长度后，所得到的对应点表示的数为（）．

A、 $- 3$ B、 $- 5$ C、 $- 3$ 或 $- 5$ D、无法确定

查看试题解析
2. a，b是有理数，它们在数轴上的位置如图所示．把a，b，﹣a，﹣b按照从小到大的顺序排列，正确的是（）

A、 $b < a < - a < - b$ B、 $- a < b < - b < a$ C、 $b < - a < a < - b$ D、 $- b < - a < a < b$

查看试题解析
3. 在数轴上，表示一个数的相反数的点不在原点的右边，则这个数是（）

A、正数 B、非负数 C、负数 D、非正数

查看试题解析
4. 在数轴上，点 $A$ 表示的数是 $- 4$ ，点 $B$ 表示的数是2，则线段 $A B$ 的长度数为（）

A、2 B、4 C、6 D、8

查看试题解析
5. 已知在数轴上点M表示的数是 $- 4$ ，点N与点M的距离是3个单位长度，则点N表示的数是．

查看试题解析
6. 数轴上表示数 $- 5$ 和表示数 $- 14$ 的两点之间的距离是；若点 $P$ 表示 $- 2$ ，则距 $P$ 点5个单位长的点表示的数是．

查看试题解析
7. 小明不慎将墨水滴在数轴上，根据图中的数值，判定墨迹盖住部分的整数的和是．

查看试题解析
8. 已知有理数 $a$ ， $b$ 所对应的点在数轴上的位置如图所示．

(1)、在数轴上表示出 $a$ ， $b$ 的相反数的位置；

(2)、若数 $b$ 对应的点与其相反数对应的点相距 $12$ 个单位长度，求 $b$ 的值；

(3)、在（ $2$ ）的条件下，若数 $a$ 对应的点与数 $b$ 的相反数对应的点相距 $2$ 个单位长度，求 $a$ 的值．

查看试题解析
9. （1）画数轴并在数轴上表示下列各数：0，3， $1.5$ ， $- 4$ ， 1， $- \frac{3}{2}$ ；
（2）按从小到大的顺序用“ $<$ ”号把（1）中的这些数连接起来；
（3）直接填空：数轴上表示3和表示1的两点之间的距离是，数轴上 $A$ 点表示的数为 $1.5$ ， $B$ 点表示的数为 $- \frac{3}{2}$ ，则点 $A$ ， $B$ 两点之间的距离是．

查看试题解析
10. 阅读理解：数轴上线段的长度可以用线段端点表示的数进行减法运算得到，如图，线段 $B C =$ 2=3-1；线段 $A B = 3 = 1 - (- 2)$ ．
问题：

(1)、数轴上点M、N代表的数分别为10和3，则线段 $M N =$ ；

(2)、数轴上点E、F代表的数分别为3和 $- 1$ ，则线段 $E F =$ ；

(3)、数轴上的两个点之间的距离为5，其中一个点表示的数为12，求另一个点表示的数．

查看试题解析
11. 如图，点 $A 、 B$ 为数轴上的两点，点 $A$ 表示 $- 8$ ，点 $B$ 表示4，点 $P$ 为数轴上一动点．

(1)、若点 $P$ 在 $A 、 B$ 之间，满足 $P B = 2 P A$ 时，求点 $P$ 表示的数；

(2)、若点 $P$ 以每秒1个单位的速度从原点开始向右运动，点 $P$ 到点 $A$ 的距离是点 $P$ 到点 $B$ 的距离的3倍时，求点 $P$ 运动的时间．

查看试题解析

二、能力提升

12. 已 $A 、 B$ 两点在数轴上表示的数分别是 $- 3$ 和 $- 6$ ，若在数轴上找一点 $C$ ，使得 $A$ 和 $C$ 之间的距离是 $4$ ，使得 $B 、 D$ 之的距离是 $1$ ，则 $C 、 D$ 之间的距离不可能是（　　）

A、 $0$ B、 $6$ C、 $2$ D、 $4$

查看试题解析
13. 有理数a、b、c在数轴上对应点的位置如图所示，若|b|＞|c|，则下列结论中正确的是（）

A、abc＜0 B、b＋c＜0 C、a＋c＞0 D、ac＞ab

查看试题解析
14. 数轴上点 $A$ ， $B$ ， $C$ ， $D$ 对应的有理数都是整数．若点 $A$ 对应有理数 $a$ ，点 $D$ 对应有理数 $d$ ，且 $2 a + d + 2 = 0$ ，则数轴上原点应是（）

A、A点 B、B点 C、C点 D、D点

查看试题解析
15. 在数轴上，若把表示数 $a$ 的点 $A$ 向右平移6个单位到达点 $B$ ，点 $B$ 表示的数恰好为 $- a$ ，则 $a$ 等于（）

A、 $- 3$ B、3 C、6 D、 $- 6$

查看试题解析
16. 如图所示，圆的周长为 $4$ 个单位长度，在圆周的 $4$ 等分点处标上字母 $A ， B ， C ， D$ ，先将圆周上的字母 $A$ 对应的点与数轴的数字 $1$ 所对应的点重合，若将圆沿着数轴向左滚动、那么数轴上的 $- 2025$ 所对应的点与圆周上重合的字母是（　　）

A、 $A$ B、 $B$ C、 $C$ D、 $D$

查看试题解析
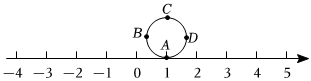17. 点P在数轴上从0开始，第1次向右移动1个单位，紧接着第2次向左移动2个单位，第3次向右移动3个单位，第4次向左移动4个单位，⋯，依此规律移动，当它移动160次时，落在数轴上的点表示的数是．

查看试题解析
18. 长方形 $A B C D$ 在数轴上的位置如图所示，点B、C对应的数分别为 $- 2$ 和 $- 1$ ， $C D = 3$ ．若长方形 $A B C D$ 绕着点C顺时针方向在数轴上翻转，翻转1次后，点D所对应的数为2；绕点D翻转第2次；继续翻转，则翻转2023次后，落在数轴上的两点所对应的数中较大的是．

查看试题解析
19. 等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和-1，若△ABC绕顶点按顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2023次后，点B对应的数是．

查看试题解析
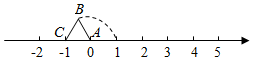20. 数轴上两点A ， B表示的数分别为a ， b ，其中 $(a + 1)^{2} + | b - 6 | = 0$ ，有一点M位于点B的左侧并与点B的距离是5，点M为线段 $A C$ 的中点.

(1)、画出数轴，并用数轴上的点表示点A ，点B ，点C ，点M；

(2)、若点P从点O出发，沿数轴以每秒2个单位长度的速度向右匀速移动，设移动时间为t秒，当 $t = 1$ 时，线段 $P M$ 的长是；此时线段PM与线段PC的数量关系是；

(3)、若点P从点A出发，沿数轴以每秒2个单位长度的速度向右匀速移动，同时点Q从点B出发，沿数轴以每秒1个单位长度的速度向左匀速移动，设移动时间为t秒．当 $P Q = 1$ 时，求t的值．

查看试题解析

三、拓展创新

21. 一点 $P$ 从距离原点1个单位的 $A$ 点处向原点方向跳动，第一次跳动到 $O A$ 的中点 $A_{1}$ 处，第二次从点 $A_{1}$ 跳动到 $O A_{1}$ 的中点 $A_{2}$ 处，第三次从点 $A_{2}$ 跳动到 $O A_{2}$ 的中点 $A_{3}$ 处，如此不断跳动下去，则第6次跳动后，则 $A_{6} A$ 的长度是（）

A、 $1 - \frac{1}{7}$ B、 $1 - \frac{1}{12}$ C、 $1 - \frac{1}{32}$ D、 $1 - \frac{1}{64}$

查看试题解析
22. 数轴上表示整数的点称为整点，某数轴的单位长度是1厘米，若在这个数轴上随意画出一条长2022厘米的线段AB，则线段AB盖住的整点共有个．

查看试题解析
23. 有理数a和b分别对应数轴上的点A和点B，定义 $M (a, b) = \frac{a + b}{2}$ 为数a、b的中点数，定义 $D (a, b) = |a - b|$ 为点A、B之间的距离，其中 $|a - b|$ 表示数a、b的差的绝对值．例如：数 $- 1$ 和3的中点数是 $M (- 1, 3) = \frac{- 1 + 3}{2} = 1$ ，数轴上表示数 $- 1$ 和3的点之间的距离是 $D (- 1, 3) = |- 1 - 3| = 4$ ．请阅读以上材料，完成下列问题：

(1)、 $M (2, 4) =$ ______， $D (2, 4) =$ ______；

(2)、已知 $M (0, x) + D (6, 8) = - 2$ ，求 $D (x, 2)$ 的值；

(3)、当 $D (- 2, 7) + D (4, x) = 13$ 时，求 $M (\frac{x - 1}{2}, 6)$ 的值．

查看试题解析