人教版数学九年级全册知识点训练营——一元二次方程的几何问题

试卷更新日期：2024-10-12 类型：复习试卷

进入出卷网下载

一、静态几何问题

1. 如图，在长为54米、宽为38米的矩形草地上修同样宽的路，余下部分种植草坪．要使草坪的面积为1800平方米，设道路的宽为x米，则可列方程为（）

A、 $(54 - x) (38 - x) = 1800$ B、 $(54 - x) (38 - x) + x^{2} = 1800$ C、 $54 \times 38 - 54 x - 38 x = 1800$ D、 $54 x + 38 x = 1800$

查看试题解析
2. 如图所示，某景区内有一块长方形油菜花田地（单位：m），现在其中修建一条观花道（阴影部分）供游人赏花，要求观花道的面积占长方形油菜花田地面积的 $\frac{1}{3}$ ．设观花道的直角边（如图所示）为x ，则可列方程为（）

A、（10+x）（9+x）＝30 B、（10+x）（9+x）＝60 C、（10﹣x）（9﹣x）＝30 D、（10﹣x）（9﹣x）＝60

查看试题解析
3. 如图，学校要在校园内建一个矩形的开心农场，其中一边 $A D$ 是围墙，且 $A D$ 的长不能超过 $28 m$ ，其余三边 $A B$ ， $B C$ ， $C D$ 用 $60 m$ 长的铁质栅栏．有下列结论：
① $A B$ 的长可以为 $15 m$ ；
②当农场 $A B C D$ 面积为 $200 m^{2}$ 时，满足条件的 $A B$ 的长只有一个值；
③农场 $A B C D$ 面积的最大值为 $450 m^{2}$ ；
④若把农场的形状改成半圆形，且直径一侧利用已有围墙，则农场的面积可以超过 $560 m^{2}$ ．
其中，正确结论的是． (只需填序号)

查看试题解析

4. 如何利用闲置纸板箱制作储物盒

如何利用闲置纸板箱制作储物盒
素材 $1$	如图 $1$ ，图中是小琴家需要设置储物盒的区域，该区域可以近似看成一个长方体，底面尺寸如图 $2$ 所示．
素材 $2$	如图是利用闲置纸板箱拆解出的①，②两种均为 $a cm (a < 50 cm)$ 长方形纸板．
	长方形纸板①	长方形纸板②

	小琴分别将长方形纸板①和②以不同的方式制作储物盒．
	长方形纸板①的制作方式	长方形纸板②制作方式
	裁去角上 $4$ 个相同的小正方形，折成一个无盖长方体储物盒．	将纸片四个角裁去 $4$ 个相同的小长方形，折成一个有盖的长方体储物盒．
目标 $1$	熟悉材料	按照长方形纸板①的制作方式制成的储物盒能够无缝障的放入储物区域，则长方形纸板宽 $a$ 为______．
目标 $2$	利用目标 $1$ 计算所得的数据 $a$ ，进行进一步探究．
	初步应用	（1）按照长方形纸板①的制作方式，为了更方便地放入或取出储物盒，盒子四周需要留出一定的空间，当储物盒的底面积是 $936 {cm}^{2}$ ，求储物盒的容积．
	储物收纳	（2）按照长方形纸板②的制作方式制作储物盒，若 $E F$ 和 $H G$ 两边恰好重合且无重叠部分，盒子的底面积为 $702 {cm}^{2}$ ．如图，是家里一个玩具机械狗的实物图和尺寸大小，请通过计算判断玩具机械狗能否完全放入该储物盒．

查看试题解析

5. 阅读下列材料，并完成相应学习任务：
一元二次方程在几何作图中的应用

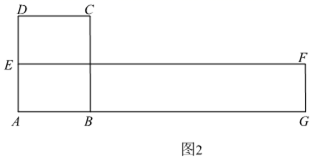
如图1，在矩形ABCD中，AB＝3，BC＝4，求作一个矩形，使其周长和面积分别是矩形ABCD的周长和面积的2倍．

因为矩形ABCD的周长是14，面积是12，所以所求作的矩形周长是28，面积是24

若设所求作的矩形一边的长为x，则与其相邻的一边长为14﹣x，所以，得x（14﹣x）＝24，解得x₁＝2，x₂＝12

当x＝2时，14﹣x＝12；当x＝12时，14﹣x＝2，所以求作的矩形相邻两边长分别是2和12

如图2，在边AB的延长线取点G，使得AG＝4AB．在AD上取AE＝ $\frac{1}{2}$ AD，以AG和AE为邻边作出矩形AGFE，则矩形AGFE的周长和面积分别是矩形ABCD的周长和面积的2倍．

学习任务：

(1)、在作出矩形AGFE的过程中，主要体现的数学思想是___________；（填出序号即可）

A、转化思想； B、数形结合思想； C、分类讨论思想； D、归纳思想

(2)、是否存在一个矩形，使其周长与面积分别是矩形ABCD的周长和面积的 $\frac{1}{2}$ ？若存在，请在图1中作出符合条件的矩形；若不存在，请说明理由．

查看试题解析

二、动态几何问题

6. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 8 c m$ ， $B C = 6 c m$ ，动点P ， Q分别从点A ， B同时开始沿 $A B$ ， $B C$ 运动（运动方向如图所示），点P的速度为 $1 c m / s$ ，点Q的速度为 $2 c m / s$ ，当点Q移动到点C时，两点同时停止运动，设运动的时间为 $t s$ ，当 $△ P B Q$ 的面积为 $12 c m^{2}$ 时，则可列方程为（）

A、 $\frac{1}{2} t (8 - t) = 12$ B、 $2 t (8 - t) = 12$ C、 $\frac{1}{2} t (8 - 2 t) = 12$ D、 $t (8 - t) = 12$

查看试题解析
7. 如图所示，A，B，C，D为矩形的四个顶点，AB=16cm，AD=8cm，动点P，Q分别从点A，C同时出发，点P以3cm/s的速度向B移动，一直到达B为止；点Q以2cm/s的速度向D移动．当P，Q两点从出发开始几秒时，点P和点Q的距离是10cm．(若一点到达终点，另一点也随之停止运动)（）

A、2s或 $\frac{23}{5}$ s B、1s或 $\frac{22}{5}$ s C、 $\frac{22}{5}$ s D、2s或 $\frac{22}{5}$ s

查看试题解析
8. 如图， $A O = B O = 50 c m ， O C$ 是一条射线， $O C ⊥ A B$ ，一只蚂蚁由点 $A$ 以 $2 c m / s$ 的速度向点 $B$ 爬行，同时另一只蚂蚁由点 $O$ 以 $3 c m / s$ 的速度沿 $O C$ 方向爬行，则经过 $s$ 后，两只蚂蚁与点 $O$ 组成的三角形的面积为 $450 {cm}^{2}$ ．

查看试题解析
9. 如图，在平面直角坐标系中，O为坐标原点，四边形 $O A B C$ 是矩形，点A ， C的坐标分别为 $A (9 ， 0)$ ， $C (0 ， 3)$ ，点D以2个单位长度/s的速度从A出发沿A至O方向向终点O运动，点P以1个单位长度/s的速度从C出发沿C至B方向向终点B运动，当 $△ O D P$ 是以 $O P$ 为一腰的等腰三角形时，点P的坐标为．

查看试题解析
10. 如图，在 Rt $△ A B C$ 中， $∠ C = 90^{\circ} ， B C = 7 c m ， A C > B C$ ．动点 $P$ 在线段 $A C$ 上并从点 $C$ 出发，沿 $C A$ 方向运动；动点 $Q$ 在线段 $B C$ 上并同时从点 $B$ 出发，沿 $B C$ 方向运动．如果点 $P ， Q$ 的运动速度均为 $1 c m / s$ ，那么运动多少秒时，它们相距 $5 c m ？$

查看试题解析
11. 如图，在Rt△ABC中，∠ACB＝90°，AB＝5cm ， BC＝3cm ，将△ABC绕点A按逆时针方向旋转90°得到△ADE ，连接CD ．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，点Q从点A出发，沿AD方向匀速运动，速度为1cm/s ，连接CP ， PQ ．设运动时间为t（s）（0＜t＜5）．解答下列问题：

(1)、当CP⊥AB时，求t的值；

(2)、设五边形BCDQP的面积为S（cm²），求S与t之间的函数关系式；

(3)、是否存在某一时刻t ，使五边形BCDQP的面积为10？若存在，求出t的值；若不存在，请说明理由．

(4)、当t＝时，PQ∥CD ．（此问只需填空）

查看试题解析
12. 在矩形 $A B C D$ 中， $A B = 5 c m$ ， $B C = 6 c m$ ，点 $P$ 从点 $A$ 开始沿边 $A B$ 向终点 $B$ 以 $1 c m / s$ 的速度移动；与此同时，点 $Q$ 从点 $B$ 开始沿边 $B C$ 向终点 $C$ 以 $2 c m / s$ 的速度移动，如果 $P$ ， $Q$ 分别从 $A$ ， $B$ 同时出发，当点 $Q$ 运动到点 $C$ 时，两点停止运动．设运动时间为 $t$ 秒．

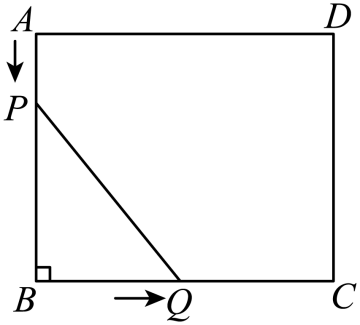(1)、填空： $B Q =$ $c m$ ， $P B =$ $c m$ （用含 $t$ 的代数式表示）；

(2)、当 $t$ 为何值时， $P Q$ 的长度等于 $5 c m$ ？

(3)、是否存在 $t$ 的值，使得五边形 $A P Q C D$ 的面积等于 $26 c m^{2}$ ？若存在，请求出此时 $t$ 的值；若不存在，请说明理由．

查看试题解析
13. 如图，在直角梯形 $A B C D$ 中， $A D ∥ C B$ ， $∠ C = 90 ° ， B C = 16 ， D C = 12 ， A D = 21$ ，动点P从点D出发，沿射线 $D A$ 的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段 $C B$ 上以每秒1个单位长的速度向点B运动，点P ， Q分别从点D ， C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．

(1)、设 $△ B P Q$ 的面积为S ，求S与t之间的函数关系式；

(2)、当t为何值时，四边形 $A B Q P$ 是平行四边形；

(3)、当t为何值时，以B ， P ， Q三点为顶点的三角形是等腰三角形?

查看试题解析