人教版数学九年级全册知识点训练营——高次方程

试卷更新日期：2024-10-12 类型：复习试卷

进入出卷网下载

1. 方程 $2 x^{3} - 2 = 0$ 的解是（）

A、 $x = - 1$ B、 $x = 0$ C、 $x = 1$ D、 $x = \pm 1$

查看试题解析
2. 若方程 $x^{2} - 2 x - 1 = 0$ 的根也是方程 $x^{3} + a x^{2} + b x + c = 0$ 的根，则 $3 a + b + c$ 的值为（）.

A、7 B、 $- 7$ C、5 D、 $- 5$

查看试题解析
3. 关于x的方程x³+x-1=0的根的情况是（　　）

A、有三个实数根 B、有两个实数根 C、有一个实数根 D、无实数跟

查看试题解析
4. 下列方程中，有实数根的是（）

A、 $x^{2} - x + 4 = 0$ B、 $\sqrt{x - 3} + 2 = 0$ C、 $\sqrt{x + 2} = - x$ D、 $\frac{x}{x^{2} - 1} = \frac{1}{x^{2} - 1}$

查看试题解析
5. 下列方程中， $x ＝ 1$ 是它的根的方程为（）

A、 $\frac{x^{2} - 1}{x - 1} = 0$ B、 $2 x^{3} - 6 = 0$ C、 $\sqrt{x} + 1 = 0$ D、 $\frac{x^{2}}{x + 1} = \frac{1}{x + 1}$

查看试题解析

6. 已知 $x^{4} - 5 x^{3} + 8 x^{2} - 5 x + 1 = 0$ ，则 $x + \frac{1}{x} =$ ．

查看试题解析
7. 方程 $x^{3} + 8 = 0$ 的解是．

查看试题解析
8. 方程 $\frac{1}{2} x^{5} + \frac{3}{2} = 0$ 的解是．（保留三位小数）．

查看试题解析
9. 方程 $x^{2} = 27 x^{3}$ 的实数解为．

查看试题解析
10. 方程 $4 x^{4} = \frac{1}{4}$ 的解是．

查看试题解析
11. 阅读材料：若 $x^{3} + 2 x^{2} - 2 x + m (m$ 为常数 $)$ 有一个因式为 $(x - 1)$ ，则如何因式分解 $x^{3} + 2 x^{2} - 2 x + m$ ？
解：因为 $x^{3} + 2 x^{2} - 2 x + m$ 有一个因式为 $(x - 1)$ ，所以当 $x - 1 = 0$ 时， $x^{3} + 2 x^{2} - 2 x + m = 0$ ，于是把 $x = 1$ 代入 $x^{3} + 2 x^{2} - 2 x + m = 0$ 得 $1 + 2 - 2 + m = 0$ ，解得 $m = - 1$ ，原代数式变为 $x^{3} + 2 x^{2} - 2 x - 1$ ，接着可以通过列竖式做多项式除法的方式求出其它因式，如图所示，则因式分解 $x^{3} + 2 x^{2} - 2 x - 1 = (x - 1) (x^{2} + 3 x + 1)$

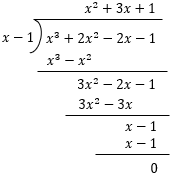
若 $x^{3} + 4 x^{2} + m x + 2 (m$ 为常数 $)$ 有一个因式为 $(x + 2)$ ，则因式分解 $x^{3} + 4 x^{2} + m x + 2 =$ .

查看试题解析