湖南省长沙市长郡教育集团2024-2025学年九年级上学期数学第一次月考试题

试卷更新日期：2024-10-10 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 如图各交通标志中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 地球上的陆地面积约为149000000平方千米，这个数字用科学记数法表示应为（）

A、0.149×10⁶ B、1.49×10⁷ C、1.49×10⁸ D、14.9×10⁷

查看试题解析
3. 下列计算正确的是（）

A、x²•x³＝x⁵ B、（x³）³＝x⁶ C、x（x+1）＝x²+1 D、（2a﹣1）²＝4a²﹣1

查看试题解析
4. 下面是2024年丽江市某周发布的最高温度：16℃， $19 ℃$ ， $22 ℃$ ， $24 ℃$ ， $26 ℃$ ， $24 ℃$ ， $23 ℃$ ．关于这组数据，下列说法正确的是（）

A、中位数是24 B、众数是24 C、平均数是20 D、方差是9

查看试题解析
5. 下列关于x的一元一次不等式 ${\begin{cases} 1 - x ＞ 0 \\ 2 x - 1 ＞ - 5 \end{cases}$ 的解集在数轴上的表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，已知AB是⊙O的直径，D、C是劣弧EB的三等分点，∠BOC＝40°，那么∠AOE＝（）

A、40° B、60° C、80° D、120°

查看试题解析
7. 关于函数y＝﹣2x+1，下列结论正确的是（）

A、图象必经过点（﹣2，1） B、图象经过第一、二、三象限 C、图象与直线y＝﹣2x+3平行 D、y随x的增大而增大

查看试题解析
8. 如图，直线AB∥CD，直线EF分别与AB，CD交于点E，F，EG平分∠BEF，交CD于点G，若∠1＝70°，则∠2的度数是（　　）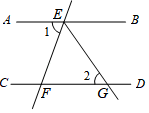

A、60° B、55° C、50° D、45°

查看试题解析
9. 函数y＝ax²+b（a≠0）与y＝ax+b（a为常数，a≠0），在同一平面直角坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D．且DC＋DA＝12， ⊙O的直径为20，则AB的长等于( )

A、8 B、12 C、16 D、18

查看试题解析

二、填空题（共6小题，满分18分，每小题3分）

11. 因式分解：﹣a²﹣6a﹣9＝．

查看试题解析
12. 请写出一个经过点（0，﹣2），且y随着x增大而增大的一次函数：．

查看试题解析
13. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示，则不等式ax²+bx+c＞0的解集是．

查看试题解析
14. 如图，石拱桥的主桥拱是圆弧形．如图，一石拱桥的跨度AB＝16m ，拱高CD＝4m ，那么桥拱所在圆的半径OA＝m ．

查看试题解析
15. 已知关于x的方程x²﹣kx﹣6=0的一个根为x=3，则实数k的值为．

查看试题解析
16. 如图，四边形ABCD内接于⊙O ，点M在AD的延长线上，∠CDM＝71°，则∠AOC＝．

查看试题解析

三、解答题（共9小题，满分72分）

17. 计算： ${(\frac{1}{2})}^{- 1} + | 1 - \sqrt{3} | - \sqrt{27} + 202 4^{0}$ ．

查看试题解析
18. 先化简，再求值：（2y+1）（2y-1）﹣（y﹣1）（y+5）-3y² ，其中y＝﹣2．

查看试题解析
19. 如图所示，每个小正方形的边长为1个单位长度，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．

(1)、点A关于点O中心对称的点的坐标为；

(2)、△AOB绕点O顺时针旋转90°后得到△A₁OB₁ ，在图中画出△A₁OB₁ ，并写出点B₁的坐标： ▲ ．

查看试题解析
20. 如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE ，连接CD ， BE ．

(1)、求证：∠AEB＝∠ADC；

(2)、连接DE ，若∠ADC＝125°，求∠BED的度数．

查看试题解析
21. 如图，在⊙O中，直径AB与弦CD相交于点P， $∠ C A B = 45 °$ ， $∠ A P D = 75 °$ ．

(1)、求 $∠ B$ 的大小；

(2)、已知圆心O到BD的距离为3，求AD的长．

查看试题解析
22. 如图，已知抛物线的顶点坐标为 $(- 1, - \frac{9}{4})$ ，与 $y$ 轴交于点 $E (0, - 2)$ ，与 $x$ 轴交于B，C两点.

(1)、求抛物线的解析式，并求出B，C两点的坐标；

(2)、在抛物线的对称轴上找一点H，使 $C H + E H$ 的值最小，求出点 $H$ 的坐标.

查看试题解析
23. 为了迎接中秋节的到来，河西某商场计划购进一批甲、乙两种月饼，已知一盒甲种月饼的进价与一盒乙种月饼的进价的和为180元，用4000元购进甲种月饼的盒数与用5000元购进乙种月饼的盒数相同.

(1)、求每盒甲种、乙种月饼的进价分别是多少元；

(2)、商场用不超过4600元的资金购进甲、乙两种月饼共50盒，其中甲种月饼的盒数不超过乙种月饼的盒数，甲种月饼售价190元，乙种月饼售价200元，为了回馈顾客，每卖一盒甲种月饼就返利顾客m元(10<m<12)，当月饼售完后，要使利润最大，对甲种、乙种月饼应该怎样进货?

查看试题解析
24. 定义：如果两个正方形满足，一个正方形的边长与另一个正方形的对角线长相等，那么称这两个正方形互为“完美嵌套”

(1)、若两个互为“完美嵌套”正方形的边长分别为a，b，则a，b满足的关系式为；

(2)、如图1，正方形ABCD和正方形AEFG互为“完美嵌套”，边AE在边AB上，且AB=12.将正方形AEFG绕点A逆时针旋转α(0°≤α≤45°)
①在旋转的过程中，当∠BEA=120°时，试求BE的长；
②BE的延长线交直线DG于点Q，当正方形AEFG由图1绕点A逆时针旋转45°，请求出在旋转过程中四边形BDQA面积的最大值.

查看试题解析
25. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与 $x$ 轴分别交于点 $A (- 1, 0)$ ， $B (3, 0)$ ，与 $y$ 轴交于点 $C (0, - 3)$ .

(1)、求二次函数的解析式；

(2)、如图1，点 $E$ 位于第四象限内的抛物线上一点，过点 $E$ 作 $E F / / y$ 轴，交 $x$ 轴于点 $F$ ，点 $H$ 在线段EF上(不与E，F重合)，连接BH.
①若BH=HE，BF：HF=3：4，求点 $E$ 的坐标；
②如图2，若点 $E$ 横坐标为2，延长BH交抛物线于点 $N$ ，连接AH并延长交抛物线于点 $M$ ，连接 $A N, B M, △ B H M$ 的面积为 $S_{1}$ ， $△ A N H$ 的面积为 $S_{2}$ ，求 $S_{1} : S_{2}$ 的值.

查看试题解析