广东省深圳市福田区红岭教育集团2023-2024学年九年级上学期数学期中试卷

试卷更新日期：2024-10-10 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 一元二次方程x²＝x的解为（）

A、﹣x＝1 B、x₁＝x₂＝1 C、x₁＝0，x₂＝1 D、x₁＝x₂＝0

查看试题解析
2. 已知 $2 x = 3 y$ （ $x y \neq 0$ ），则下列比例式成立的是（）

A、 $\frac{x}{2} = \frac{3}{y}$ B、 $\frac{x}{3} = \frac{y}{2}$ C、 $\frac{x}{y} = \frac{2}{3}$ D、 $\frac{y}{x} = \frac{3}{2}$

查看试题解析
3. 随机掷一枚均匀的硬币两次，落地后至少有一次正面朝上的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 菱形，矩形，正方形都具有的性质是（　　）

A、四条边相等，四个角相等 B、对角线相等 C、对角线互相垂直 D、对角线互相平分

查看试题解析
5. 方程x²﹣8x+15=0左边配成一个完全平方式后，所得的方程是（）

A、（x﹣6）²=1 B、（x﹣4）²=1 C、（x﹣4）²=31 D、（x﹣4）²=﹣7

查看试题解析
6. 如图，平面直角坐标系中，点C位于第一象限，点B位于第四象限，四边形OABC是边长为1的正方形，OC与x轴正半轴的夹角为15°，则点B的纵坐标为（）

A、﹣2 B、 $- \frac{\sqrt{2}}{2}$ C、 $- \frac{\sqrt{2}}{3}$ D、 $- \frac{1}{2}$

查看试题解析
7. 如图，正方形ABCD外取一点E ，连接AE、BE、DE ．过点A作AE的垂线交DE于点P ，若AE＝AP＝1，PB＝ $\sqrt{3}$ ．下列结论：①EB⊥ED；②点B到直线DE的距离为 $\frac{\sqrt{2}}{2}$ ；③S_△_APD+S_△_APB＝ $\frac{\sqrt{2} + 1}{2}$ ；④S_正方形_ABCD＝2+ $\sqrt{2}$ ．其中正确结论的序号是（）

A、①③④ B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题（每题3分，共15分）

8. 将方程（2x+1）（x﹣3）＝x²+1化为一般形式，可知一次项系数为．

查看试题解析
9. 如图， $A D ∥ B E ∥ C F$ ，直线 $l_{1}$ 、 $l_{2}$ 与这三条直线分别交于点A、B、C和D、E、F，若 $A B = 6$ ， $B C = 3$ ， $D F = 12$ ，则DE的长为．

查看试题解析
10. 已知a是方程x²﹣3x﹣1011＝0的一个根，则代数式2a²﹣6a+1的值是．

查看试题解析
11. 在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机抽出一个球.记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球个.

查看试题解析
12. 如图，在Rt△ABC和Rt△ABD中，∠ACB＝∠ADB＝90°，AB＝10，M是AB的中点，连接MC ， MD ， CD ，若CD＝6，则△MCD的面积．

查看试题解析

三、解答题（共55分）

13. 解方程：

(1)、x（x+2）＝2（x+2）；

(2)、3x²﹣x﹣1＝0．

查看试题解析
14. 已知，△ABC在直角坐标系内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）（正方形网格中每个小正方形的边长均为一个单位长度）．
①画出△ABC向下平移4个单位得到的△A₁B₁C₁；
②以点B为位似中心，在网格内画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2：1；
③△A₃B₃C₃与△A₁B₁C₁是位似图形，位似中心为原点，位似比为3：2，若M（a ， b）为线段A₁C₁上任一点，写出点M对应点M₂的坐标．

查看试题解析
15. 某校在课后服务中，成立了以下社团： $A .$ 计算机， $B .$ 围棋， $C .$ 篮球， $D .$ 书法每人只能加入一个社团，为了解学生参加社团的情况，从参加社团的学生中随机抽取了部分学生进行调查，并将调查结果绘制成如下两幅不完整的统计图，其中图 $1$ 中 $D$ 所占扇形的圆心角为 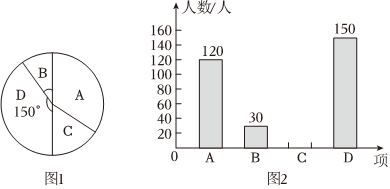$150 °$ ．
请结合图中所给信息解答下列问题：

(1)、这次被调查的学生共有人；

(2)、请你将条形统计图补充完整；

(3)、若该校共有 $1800$ 学生加入了社团，请你估计这 $1800$ 名学生中有多少人参加了篮球社团；

(4)、在书法社团活动中，由于甲、乙、丙、丁四人平时的表现优秀，恰好四位同学中有两名是男同学，两名是女同学 $.$ 现决定从这四人中任选两名参加全市书法大赛，用画树状图求恰好选中一男一女的概率．

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中， $B D ⊥ A B$ ，延长 $A B$ 至点E，使 $B E = A B$ ，连接 $E C$ ．

(1)、求证：四边形 $B E C D$ 是矩形．

(2)、连接 $A C$ ，若 $A D = 3 ， C D = 2$ ，求 $A C$ 的长．

查看试题解析
17. 某商店销售一款工艺品，平均每天可销售20件，每件盈利40元，为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，在一定范围内，每件工艺品的单价每降价1元，商场平均每天可多售出2件．

(1)、如果商店通过销售这种工艺品每天想盈利1050元，那么每件工艺品单价应降多少元？

(2)、能否通过降价使商店每天盈利达到1600元？请说明理由．

查看试题解析
18. 已知：RT△ABC与RT△DEF中，∠ACB＝∠EDF＝90°，∠DEF＝45°，EF＝8cm ， AC＝16cm ， BC＝12cm ．现将RT△ABC和RT△DEF按图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，并按如下方式运动．
运动一：如图2，△ABC从图1的位置出发，以1cm/s的速度沿EF方向向右匀速运动，DE与AC相交于点Q ，当点Q与点D重合时暂停运动；
运动二：在运动一的基础上，如图3，RT△ABC绕着点C顺时针旋转，CA与DF交于点Q ， CB与DE交于点P ，此时点Q在DF上匀速运动，速度为 $\sqrt{2} c m / s$ ，当QC⊥DF时暂停旋转；
运动三：在运动二的基础上，如图4，RT△ABC以1cm/s的速度沿EF向终点F匀速运动，直到点C与点F重合时为止．
设运动时间为t（s），中间的暂停不计时，
解答下列问题

(1)、在RT△ABC从运动一到最后运动三结束时，整个过程共耗时s；

(2)、在整个运动过程中，设RT△ABC与RT△DEF的重叠部分的面积为S（cm²），求S与t之间的函数关系式，并直接写出自变量t的取值范围；

(3)、在整个运动过程中，是否存在某一时刻，点Q正好在线段AB的中垂线上，若存在，求出此时t的值；若不存在，请说明理由．

查看试题解析
19. 如图所示的一张矩形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与C重合，再展开，折痕EF交AD边于点E ，交BC边于点F ，交AC于点O ，分别连接AF和CE ．

(1)、求证：四边形AFCE是菱形；

(2)、过E点作AD的垂线EP交AC于点P ，求证：2AE²＝AC•AP；

(3)、若AE＝10cm ， △ABF的面积为24cm² ，求△ABF的周长．

查看试题解析