【基础版】北师大版数学九年级上册第六章反比例函数章节测试卷

试卷更新日期：2024-10-10 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共24分）

1. 若函数 $y = \frac{k}{x}$ 的图象经过点 $A (3 ， - 4)$ ，则 $k$ 的值为（）

A、6 B、 $- 6$ C、12 D、 $- 12$

查看试题解析
2. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{1}{x}$ 的图象交于 $(- 1 ， m)$ ， $(- 5 ， n)$ 两点，则不等式 $k x + b - \frac{1}{x} > 0$ 的解集为（）

A、 $x < - 5$ B、 $x > - 1$ C、 $- 5 < x < - 1$ D、 $x < - 5$ 或 $- 1 < x < 0$

查看试题解析
3. 在同一平面直角坐标系中，函数 $y = k x + 1 (k \neq 0)$ 和 $y = \frac{k}{x} (k \neq 0)$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
4. 如图，双曲线 $y = \frac{k}{x}$ 与直线 $y = 2 x$ 相交于A、B两点，点A坐标为 $(1 ， 2)$ ，则点B坐标为（）

A、 $(- 1 ， - 2)$ B、 $(1 ， 2)$ C、 $(- 1 ， 2)$ D、 $(1 ， - 2)$

查看试题解析
5. 已知蓄电池两端电压 $U$ 为定值，电流 $I$ 与 $R$ 的函数关系为 $I = \frac{U}{R} .$ 当 $I = 3 A$ 时， $R = 8 Ω$ ，则当 $I = 6 A$ 时， $R$ 的值为（）

A、 $4 Ω$ B、 $6 Ω$ C、 $8 Ω$ D、 $10 Ω$

查看试题解析
6. 如图，点P是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上任意一点，过点P作 $P M ⊥ x$ 轴，垂足为M ，若 $△ P O M$ 的面积等于4，则k的值等于（）

A、8 B、 $- 8$ C、4 D、 $- 4$

查看试题解析
7. 公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即：阻力×阻力臂＝动力×动力臂．小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是1200N和0.5m ，则动力F（单位：N）关于动力臂l（单位：m）的函数解析式正确的是（　　）

A、F＝ $\frac{1200}{l}$ B、F＝ $\frac{600}{l}$ C、F＝ $\frac{500}{l}$ D、F＝ $\frac{0.5}{l}$

查看试题解析
8. 一次函数 $y = a x - a$ 与反比例函数 $y = \frac{a}{x} (a \neq 0)$ 在同一平面直角坐标系中的图象可能是（　　　）

A、 B、 C、 D、

查看试题解析

二、填空题（每题3分，共15分）

9. 如图，点 $P$ 在反比例函数 $y = \frac{k}{x}$ 的图象上， $P A ⊥ x$ 轴于点 $A$ ， $△ P A O$ 的面积为3，则 $k$ 的值为．

查看试题解析
10. 若函数 $y = (m - 1) x^{m^{2} - 2}$ 是反比例函数，则 $m$ 的值等于．

查看试题解析
11. 如图，在平面直角坐标系中，函数 $y = \frac{5}{x} (x > 0)$ 与y＝x-1的图象交于点P（a ， b），则代数式 $\frac{1}{a} - \frac{1}{b}$ 的值为．

查看试题解析
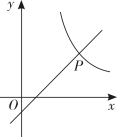12. 如图，等边△ABO的顶点O与原点重合，点A的坐标是（-4，0），点B在第二象限．反比例函数 $y = \frac{k}{x}$ 的图象经过点B，则k的值是．

查看试题解析
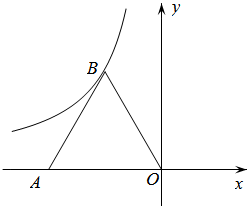13. 已知反比例函数 $y = \frac{1}{x}$ 的图像上的三点 $(- 2 ， y_{1}) ， (- 1 ， y_{2}) ， (1 ， y_{3})$ ，判断 $y_{1} ， y_{2} ， y_{3}$ 的大小关系：（用“＜”连接）

查看试题解析

三、解答题（共7题，共61分）

14. 如图所示的双曲线是函数 $y = \frac{m - 3}{x} (m$ 为常数， $x > 0$ )图象的一支若该函数的图象与一次函数 $y = x + 1$ 的图象在第一象限的交点为 $A (2 ， n)$ ，求点A的坐标及反比例函数的表达式.

查看试题解析
15. 如图，反比例函数 $y = \frac{k}{x}$ （ $k \neq 0$ ）的图像与正比例函数 $y = 2 x$ 的图像相交于 $A (1, a)$ 、 $B$ 两点，点 $C$ 在第四象限， $B C ∥ x$ 轴．

(1)、求 $k$ 的值；

(2)、以 $A B 、 B C$ 为边作菱形 $A B C D$ ，求 $D$ 点坐标及菱形的面积．

查看试题解析
16. 如图，在平面直角坐标系中，直线 $y = k x + 2 (k \neq 0)$ 与 $x$ 轴、 $y$ 轴分别交于点 $A (\frac{3}{2} ， 0)$ ，点 $D$ ，与反比例函数 $y = \frac{m}{x} (m \neq 0)$ 的图象交于点 $B (n ， 4)$ ．

(1)、求直线与反比例函数的表达式；

(2)、过点 $B$ 作 $B C ⊥ x$ 轴于点 $C$ ，若点 $P$ 在反比例函数 $y = \frac{m}{x}$ 的图象上，且 $△ P A C$ 的面积为3，求点 $P$ 的坐标．

查看试题解析
17. 某工厂生产化肥的总任务一定，平均每天化肥产量y（吨）与完成生产任务所需要的时间x（天）之间成反比例关系，如果每天生产化肥125吨，那么完成总任务需要7天.

(1)、求y关于x的函数表达式，并指出比例系数；

(2)、若要5天完成总任务，则每天产量应达到多少？

查看试题解析
18. 已知y与x成反比例，且当x＝2时，y＝﹣3．

(1)、求y关于x的函数解析式；

(2)、直接写出：当x为何值时，y＞﹣3？

查看试题解析
19. 如图，反比例函数 $y = \frac{a}{x}$ 的图像经过点 $A (- 2 ， 2)$ ，一次函数 $y = k x + b (k \neq 0)$ 的图像经过点 $A$ 且与反比例函数图象的另一个交点为 $B (1 ， n)$ ．

(1)、求一次函数与反比例函数的解析式，并在图中画出该一次函数的图象；

(2)、结合图像，直接写出不等式组 $\frac{a}{x} \leq k x + b$ 的解集．

(3)、把 $y = k x + b (k \neq 0)$ 的图像向下平移4个单位长度，若平移后的直线与反比例函数的图象在第三象限交于点 $C (- 1 ， m)$ ，求 $△ A B C$ 的面积．

查看试题解析
20. 如图，一次函数 $y = k x + b (k \neq 0)$ 与反比例函数 $y = \frac{m}{x} (m \neq 0)$ 的图象相交于A、B两点，过点B作 $B C ⊥ x$ 轴，垂足为C，连接 $A C$ ，已知点A的坐标是 $(2 ， 3)$ ， $B C = 2$ ．

(1)、求反比例函数与一次函数的关系式．

(2)、根据图象，直接写出不符式 $k x + b > \frac{m}{x}$ 的解集．

(3)、点P为反比例函数 $y = \frac{m}{x}$ 在第一象限图象上的一点，若 $S_{△ P O C} = 2 S_{△ A B C}$ ，直接写出点P的坐标．

查看试题解析

【基础版】北师大版数学九年级上册 第六章 反比例函数 章节测试卷

一、选择题（每题3分，共24分）

二、填空题（每题3分，共15分）

三、解答题（共7题，共61分）

【基础版】北师大版数学九年级上册第六章反比例函数章节测试卷