【培优版】北师大版数学九年级上册6.3反比例函数的应用同步练习

试卷更新日期：2024-10-10 类型：同步测试

进入出卷网下载

一、选择题

1. 如图表示两种材料的电阻 $R (Ω)$ 与温度 $T (℃)$ 的关系，下列说法错误的是（）

A、当 $T = a$ 时，两种材料的电阻大小相同 B、两种材料的电阻都是随着温度的增大而减小 C、当温度低于 $a ℃$ 时，半导体热敏电阻的电阻值在 $b Ω$ 以上 D、当铂热电阻的电阻值超过 $b Ω$ 时，温度在 $a ℃$ 以上

查看试题解析
2. 伟大的古希腊哲学家、数学家、物理学家阿基米德有句名言：“给我一个支点，我可以撬动地球！”这句名言道出了“杠杆原理”的意义和价值．“杠杆原理”在实际生产和生活中，有着广泛的运用．比如：小明用撬棍撬动一块大石头，运用的就是“杠杆原理”．已知阻力 $F_{1} (N)$ 和阻力臂 $L_{1} (m)$ 的函数图象如图所示，若小明想使动力 $F_{2}$ 不超过 $120 N$ ，则动力臂 $L_{2}$ （单位：m）需满足（）

A、 $L_{2} < 5$ B、 $L_{2} > 5$ C、 $L_{2} \geq 5$ D、 $0 < L_{2} \leq 5$

查看试题解析
3. 如图所示，小亮设计了一个探究杠杆平衡条件的实验：在一根匀质的木杆中点O左侧固定位置B处悬挂重物A ，右侧用一个弹簧测力计向下拉，改变弹簧测力计与支点O的距离 $x (c m),$ ，观察弹簧测力计的示数 $y (N)$ 的变化情况．实验数据记录如下表：
$x (c m),$
……
10
15
20
25
30
……
$y (N)$
……
45
30
22.5
18
15
……
下列说法不正确的是（）

A、弹簧测力计的示数 $y (N)$ 与支点O的距离 $x (c m),$ 之间关系的图象如图 B、y与x的函数关系式为 $y = \frac{450}{x} (x > 0)$ C、当弹簧测力计的示数为 $12.5 N$ 时，弹簧测力计与O点的距离是37.5 D、随着弹簧测力计与O点的距离不断增大，弹簧测力计上的示数不断减小

查看试题解析
4. 某品牌自动饮水机，开机加热时每分钟上升 $10 ℃$ ，加热到 $100 ℃$ ，停止加热，水温开始下降．此时水温 $y (℃)$ 与通电时间 $x (m i n)$ 成反比例关系．当水温降至 $20 ℃$ 时，饮水机再自动加热，若水温在 $20 ℃$ 时接通电源，水温 $y$ 与通电时间 $x$ 之间的关系如图所示，则下列说法中正确的是（）

A、上午 $8$ 点接通电源，可以保证当天 $9 ： 30$ 能喝到不超过 $40 ℃$ 的水 B、水温下降过程中， $y$ 与 $x$ 的函数关系式是 $y = \frac{400}{x}$ C、水温从 $20 ℃$ 加热到 $100 ℃$ ，需要 $7 m i n$ D、水温不低于 $30 ℃$ 的时间为 $\frac{77}{3} m i n$

查看试题解析
5. 如图，一次函数y=ax+b的图象与x轴、y轴交于A、B两点，与反比例函数 $y = \frac{k}{x}$ 的图象相交于C、D两点，分别过C、D两点作y轴，x轴的垂线，垂足为E、F，连接CF、DE，有下列结论：①△CEF与△DEF的面积相等；②EF∥CD；③△DCE≌△CDF；④AC=BD；⑤△CEF的面积等于 $\frac{k}{2}$ ，其中正确的个数有（）

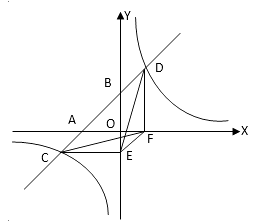A、2 B、3 C、4 D、5

查看试题解析
6. 如图所示为某新款茶吧机，开机加热时每分钟上升 $20 ℃$ ，加热到 $100 ℃$ ，停止加热，水温开始下降，此时水温 $y (℃)$ 与通电时间 $x (min)$ 成反比例关系．当水温降至 $20 ℃$ 时，饮水机再自动加热，若水温在 $20 ℃$ 时接通电源，水温y与通电时间x之间的关系如图所示，则下列说法中错误的是（　　）

A、水温从 $20 ℃$ 加热到 $100 ℃$ ，需要 $4 min$ B、水温下降过程中，y与x的函数关系式是 $y = \frac{400}{x}$ C、上午10点接通电源，可以保证当天 $10 : 30$ 能喝到不低于 $38 ℃$ 的水 D、在一个加热周期内水温不低于 $40 ℃$ 的时间为 $7 min$

查看试题解析
7. 某商家设计了一个水箱水位自动报警仪，其电路图如图1所示，其中定值电阻 $R_{1} = 10 Ω, R_{2}$ 是一个压敏电阻，用绝缘薄膜包好后放在一个硬质凹形绝缘盒中，放入水箱底部，受力面水平，承受水压的面积 $S$ 为 $0.01 m^{2}$ ，压敏电阻 $R_{2}$ 的阻值随所受液体压力 $F$ 的变化关系如图2所示（水深 $h$ 越深，压力 $F$ 越大），电源电压保持6V不变，当电路中的电流为0.3A时，报警器（电阴不计）开始报警，水的压强随深度变化的关系图象如图3所示（参考公式x $I = \frac{U}{R}, F = p S, 1000 P a$ $= 1 k P a$ ），则下列说法中不正确的是（）

A、当水箱未装水（h=0m）时，压强 $p$ 为0kPa B、当报警器刚好开始报警时，水箱受到的压力 $F$ 为40N C、当报警器刚好开始报警时，水箱中水的深度 $h$ 是0.8m D、若想使水深1m时报警，应使定值电阻 $R_{1}$ 的阻值为 $12 Ω$

查看试题解析

二、填空题

8. 青藏铁路是当今世界上海拔最高、线路最长的高原铁路，因路况、季节、天气等原因行车的平均速度在 $250 ~ 360$ （千米/小时）之间变化，铁路运行全程所需要的时间（小时）与运行的平均速度（千米/小时）满足如图所示的函数关系，列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差小时．

查看试题解析
9. 如图，已知直线y=k₁x与双曲线y= $\frac{k_{1}}{x}$ 交于A B两点，将线段AB绕点A沿顺时针方向旋转60°后，点B落在点C处，双曲线y= $\frac{k_{2}}{x}$ 经过点C，则 $\frac{k_{2}}{k_{1}}$ 的值是。

查看试题解析
10. 如图，直线y= $\frac{1}{2}$ x+4与x轴、y轴交于4、B两点，AC⊥AB，交双曲线y= $\frac{k}{x}$ (x<0)于C点，且BC交x轴于M点，BM=2CM，则k=。

查看试题解析
11. 如图是某种电子理疗设备工作原理的示意图，其开始工作时的温度是 $20 ℃$ ，然后按照一次函数关系一直增加到 $70 ℃$ ，这样有利于打通病灶部位的血液循环，在此温度下再沿反比例函数关系缓慢下降至 $35 ℃$ ，然后在此基础上又沿着一次函数关系一直将温度升至 $70 ℃$ ，再在此温度下沿着反比例函数关系缓慢下降至， $35 ℃$ 如此循环下去．

(1)、t的值为；

(2)、如果在 $0 ∼ t$ 分钟内温度大于或等于 $50 ℃$ 时，治疗效果最好，则维持这个温度范围的持续时间为分钟．

查看试题解析
12. 如图1，将一个长方体放置于一水平桌面上，按不同的方式摆放，记录桌面所受压强与受力面积的关系如下表所示：
桌面所受压强 p(Pa)
400
500
800
1000
1250
受力面积S(m²)
0.5
0.4
a
0.2
0.16

(1)、根据表中数据，计算a的值为.

(2)、将另一个长、宽、高分别为 60 cm， 20cm，10cm，且与原长方体重量相同的长方体按照如图2所示的方式放置于该水平桌面上，则桌面所承受的压强为Pa.

查看试题解析

三、解答题

13. 综合与实践：如何称量一个 $1$ 元硬币的重量？
素材 $1$ ：如图是一架自制天平，左侧托盘固定在点 $A$ 处，右侧托盘的点 $P$ 可以在横梁 $B C$ 段滑动 $.$ 已知 $A C = 30 c m ， B C = 76 c m$ ，支点 $O 在 A C$ 的中点处，一个 $100 g$ 的砝码．
素材 $2$ ：由于一个硬币太轻，这个自制天平无法直接称量，小组进行如下操作：左侧托盘放置一个 $100 g$ 砝码，右侧托盘放入 $10$ 个相同的 $1$ 元硬币，调整点 $P$ 的位置，发现当 $P C = 10 c m$ 时，天平平衡．
链接：根据杠杆原理，平衡时：左盘砝码重量 $\times O A =$ 右盘物体重量 $\times O P . ($ 不计托盘与横梁重量 $)$

(1)、任务 $1$ ：左侧托盘放入 $1 个 100 g$ 砝码，设右侧托盘放置 $y g$ 物体， $O P$ 长为 $x c m$ ，求 $y$ 关于 $x$ 的函数表达式；

(2)、任务 $2$ ：求一个 $1$ 元硬币的重量；并判断左侧托盘放入 $1 个 100 g$ 砝码时，右侧托盘至少要放置几个 $1$ 元硬币，该天平才能保持平衡；

(3)、任务 $3$ ：横梁 $A B$ 长度保持不变的情况下，通过调整天平支点的位置，使左侧托盘放入 $1 个 100 g$ 砝码，右侧托盘放置一个 $1$ 元硬币时，天平能保持平衡， $O A$ 的长度至多是多少 $c m$ ？

查看试题解析
14. 某公司的饮水机在水温为20℃时开机加热，加热时每分钟上升20℃，加热到100℃停止加热，水温开始下降，此时水温 $y$ （℃）与开机后用时 $x$ （min）成反比例关系，如图所示，直至水温降至20℃，饮水机关机（这是一个加热周期），饮水机关机后即刻自动开机，重复上述自动程序.

(1)、将水从20℃加热到100℃需要min；在图15中的水温下降的过程中，求水温 $y$ 与开机后用时 $x$ 的函数解析式（不写自变量 $x$ 的取值范围）；

(2)、在一个加热周期中，求水温不低于40℃的时长；

(3)、王经理去接水时看到饮水机的水温刚好降到50℃，若他想接到60℃的水（在不打断加热周期的情况下），请直接写出他至少还要等待多长时间？

查看试题解析
15. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = 2 x + 4$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象相交于 $A (a, - 2)$ ， $B$ 两点．

(1)、求反比例函数的表达式；

(2)、点 $C$ 是反比例函数第一象限图象上一点，且 $△ A B C$ 的面积是 $△ A O B$ 面积的一半，直接写出点 $C$ 的横坐标．

查看试题解析
16. 某农户共摘收水蜜桃1920千克，为寻求合适的销售价格，进行了6天试销，试销情况如下：

第1天
第2天
第3天
第4天
第5天
第6天
售价
x（元/千克）
20
18
15
12
10
9
销售量
y（千克）
45
50
60
75
90
100
由表中数据可知，试销期间这批水蜜桃的每天销售量y（千克）与售价x（元/千克）之间满足我们曾经学过的某种函数关系．若在这批水蜜桃的后续销售中，每天的销售量y（千克）与售价x（元/千克）之间都满足这一函数关系．

(1)、你认为y与x之间满足什么函数关系？并求y关于x的函数表达式．

(2)、在试销6天后，该农户决定将这批水密桃的售价定为15元/千克．
① 若每天都按15元/千克的售价销售，则余下的水蜜桃预计还要多少天可以全部售完？
② 该农户按15元/千克的售价销售20天后，发现剩下的水蜜桃过于成熟，必须在不超过2天内全部售完，因此需要重新确定一个售价，使后面2天都按新的售价销售且能如期全部售完，则新的售价最高可以定为多少元/千克？

查看试题解析
17. 阅读下列材料：
实验数据显示，一般成人喝250毫升低度白酒后，其血液中酒精含量（毫克/百毫升）随时间的增加逐步增高达到峰值，之后血液中酒精含量随时间的增加逐渐降低．
小带根据相关数据和学习函数的经验，对血液中酒精含量随时间变化的规律进行了探究，发现血液中酒精含量y是时间x的函数，其中y表示血液中酒精含量（毫克/百毫升），x表示饮酒后的时间（小时）．
下表记录了6小时内11个时间点血液中酒精含量y（毫克/百毫升）随饮酒后的时间x（小时）（x＞0）的变化情况．
下面是小带的探究过程，请补充完整：

(1)、如图，在平面直角坐标系xOy中，以上表中各对数值为坐标描点，图中已给出部分点，请你描出剩余的点，画出血液中酒精含量y随时间x变化的函数图象；

(2)、观察表中数据及图象可发现此函数图象在直线 $x = \frac{3}{2}$ 两侧可以用不同的函数表达式表示，请你任选其中一部分写出表达式；

(3)、按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：30在家喝完250毫升低度白酒，第二天早上7：00能否驾车去上班？请说明理由．

查看试题解析