【提升版】北师大版数学九年级上册6.3反比例函数的应用同步练习

试卷更新日期：2024-10-10 类型：同步测试

进入出卷网下载

一、选择题

1. 当温度不变时，某气球内的气压 $p (kPa)$ 与气体体积 $V (m^{3})$ 的函数关系如图所示，已知当气球内的气压 $p > 120 kPa$ 时，气球将爆炸，为了安全起见，气球的体积 $V$ 应(　　)

A、不大于 $\frac{4}{5} m^{3}$ B、大于 $\frac{4}{5} m^{3}$ C、不小于 $\frac{4}{5} m^{3}$ D、小于 $\frac{4}{5} m^{3}$

查看试题解析
2. 在四个密闭容器中分别装有甲、乙、丙、丁四种气体，如图，用四个点分别描述这四种气体的密度 $ρ (k g / m^{2})$ 与体积 $V (m^{2})$ 的情况，其中描述乙、丁两种气体情况的点恰好在同一个反比例函数的阁象上，则这四种气体的质量最小的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 某个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．如图所示的是该台灯的电流 $I (A)$ 与电阻 $R (Ω)$ 的关系图象，该图象经过点 $P (880 ， 0.25)$ ．根据图象可知，下列说法正确的是（）

A、当 $I = 0.2$ 时， $R = 1000$ B、I与R的函数表达式是 $I = \frac{200}{R} (R > 0)$ C、当 $R > 500$ 时， $I > 0.44$ D、当 $880 < R < 1000$ 时，则 $0.22 < I < 0.25$

查看试题解析
4. 在物理学中，功率表示做功的快慢，功与做功时间的比叫做功率，即所做的功一定时，功率 $P (w)$ 与做功所用的时间 $t (s)$ 成反比例函数关系，图象如图所示，下列说法不正确的是（）

A、P与t的函数关系式为 $P = \frac{60000}{t}$ B、当 $t = 5 s$ 时， $P = 12000 w$ C、当 $t > 5 s$ 时， $P > 12000 w$ D、p随t的增大而减小

查看试题解析
5. 已知经过闭合电路的电流 $I$ （单位： $A$ ）与电路的电阻 $R$ （单位： $Ω$ ）之间的关系如表所示，则下列说法中错误的是（）
$I / A$
……
5
4
$\frac{10}{3}$
$m$
2
1
0.5
0.25
……
$R / Ω$
……
20
25
30
40
50
100
200
400
……

A、 $m$ 的值为2.5 B、 $I$ 与 $R$ 之间的函数表达式为 $I = \frac{100}{R}$ C、当 $I \leq 20 A$ 时， $R \leq 5 Ω$ D、 $I$ 随 $R$ 的增大而减小

查看试题解析
6. 在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强p（kPa）与汽缸内气体的体积V（mL）成反比例，p关于V的函数图象如图所示．若压强由75kPa加压到100kPa，则气体体积压缩了（　　）

A、10mL B、15mL C、20mL D、25mL

查看试题解析
7. 物理兴趣小组在实验室研究电学时设计了一个电路，其电路图如图1所示．经测试，发现电流I（A）随着电阻R（Ω）的变化而变化，并结合数据描点，连线，画成图2所示的函数图象．若该电路的最小电阻为1Ω，则该电路能通过的（）

A、最大电流是36A B、最大电流是27A C、最小电流是36A D、最小电流是27A

查看试题解析
8. 某品牌自动饮水机，开机加热时每分钟上升 $10 ℃$ ，加热到 $100 ℃$ ，停止加热，水温开始下降．此时水温 $y (℃)$ 与通电时间 $x (m i n)$ 成反比例关系．当水温降至 $20 ℃$ 时，饮水机再自动加热，若水温在 $20 ℃$ 时接通电源，水温 $y$ 与通电时间 $x$ 之间的关系如图所示，则下列说法中正确的是（）

A、上午 $8$ 点接通电源，可以保证当天 $9 ： 30$ 能喝到不超过 $40 ℃$ 的水 B、水温下降过程中， $y$ 与 $x$ 的函数关系式是 $y = \frac{400}{x}$ C、水温从 $20 ℃$ 加热到 $100 ℃$ ，需要 $7 m i n$ D、水温不低于 $30 ℃$ 的时间为 $\frac{77}{3} m i n$

查看试题解析

二、填空题

9. 学校科技兴趣小组为探索如图所示的电路中电压 $U (V)$ 、电流 $I (A)$ 、电阻 $R (Ω)$ 三者之间的关系，测得数据如下，根据数据猜想得到三者之间为： $I = \frac{U}{R}$ ．由此可得，当电阻 $R = 110 Ω$ 时，电流 $I =$ A．
$R (Ω)$
$100$
$200$
$220$
$400$
$I (A)$
$2.2$
$1.1$
$0.55$

查看试题解析
10. 饮水机中原有水的温度为 $20 ℃$ ，通电开机后，饮水机自动开始加热(此过程中，水温 $y ℃$ 与开机时间 $x$ 分满足一次函数关系)，当加热到 $100 ℃$ 时自动停止加热，随后水温开始下降(此过程中，水温 $y ℃$ 与开机时间x分成反比例函数关系)，当水温降至 $20 ℃$ 时，饮水机又自动开始加热，……如此循环下去(如图所示)．那么开机后 $56$ 分钟时，水的温度是 $℃$ ．

查看试题解析
11. 如图，直线 $y = - x + 6$ 与y轴交于点A ，与反比例函数 $y = \frac{k}{x}$ 图象交于点C ，过点C作 $C B ⊥ x$ 轴于点B ， $A O = 3 B O$ ，则k的值为．

查看试题解析
12. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{1}{x}$ 的图象交于 $(- 1 ， m)$ ， $(- 5 ， n)$ 两点，则不等式 $k x + b - \frac{1}{x} > 0$ 的解集为．

查看试题解析
13. 小明要把一篇文章录入电脑，所需时间y（min）与录入文字的速度x（字/min）之间的函数关系如图所示．如果小明要在7min内完成录入任务，那么他录入文字的速度至少为字/min．

查看试题解析

三、解答题

14. 如图，一次函数 $y = k x + b$ 的图象与反比例的数 $y = \frac{m}{x} (x > 0)$ 的图象交于点 $A (2 n - 1 ， 6)$ 和点 $B (3 ， 3 n - 1)$ ，与x轴交于点C．

(1)、求一次函数和反比例函数的表达式；

(2)、连接 $O A$ ， $O B$ ，求 $△ A O B$ 的面积；

(3)、直接写出关于x的不等式： $\frac{m}{x} > k x + b$ 的解集．

查看试题解析
15. 如图，在平面直角坐标系中，反比例函数 $y = \frac{n}{x} (n \neq 0)$ 与一次函数 $y = k x + b (k \neq 0)$ 的图象相交于 $A (4, m), B (- 12, - 3)$ 两点，直线 $A B$ 交y轴于点C ．

(1)、求反比例函数与一次函数的表达式；

(2)、直接写出关于x的不等式 $k x + b > \frac{n}{x}$ 的解集为．

查看试题解析
16. 建筑是一门不断演化和创新的艺术，近年来，一种名为双曲铝单板的新兴材料以其独特的曲线和光泽，为建筑注入了新的时尚元素，同时也赋予了建筑更多的创意和流动性．图1为某厂家设计制造的双曲铝单板建筑，其横截面（图2）由两条曲线 $E G$ ， $F H$ （反比例函数图象的一部分）和若干线段围成，为轴对称图形，其中四边形 $A B D C$ 与四边形 $G M N H$ 均为矩形， $A B = 2 m$ ， $B E = 2 m$ ， $A C = 20 m$ ， $G M = 10 m$ ， $M N = 4 m$ ，以AC的中点 $O$ 为原点， $A C$ 所在直线为 $x$ 轴建立平面直角坐标系．

请回答下列问题：

(1)、如图2，求 $E G$ 所在图象的函数表达式．

(2)、如图3，为在曲面实现自动化操作，工程师安装了支架 $E G$ ，并加装了始终垂直于 $E G$ 的伸缩机械臂 $P Q$ 用来雕刻 $E G$ 所在曲面的花纹，请问点P在 $E G$ 上滑动过程中， $P Q$ 最长为多少米？

查看试题解析
17. 通过实验研究发现：初中生在数学课上听课注意力指标数随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散．学生注意力指标数y随时间x（分）变化的函数图象如图所示．当 $0 \leq x < 10$ 和 $10 \leq x < 20$ 时，图象是线段：当 $20 \leq x \leq 40$ 时，图象是双曲线的一部分，根据函数图象回答下列问题：

(1)、点A的注意力指标数是；

(2)、当 $0 \leq x < 10$ 时，求注意力指标数y随时间x（分）的函数解析式；

(3)、张老师在一节课上讲解一道数学综合题需要 $20$ 分钟，他能否经过适当的安排，使学生在听这道综合题的讲解时，注意力指标数都不低于 $36$ ？请说明理由．

查看试题解析
18. 驾驶员血液中每毫升的酒精含量大于或等于 $200$ 微克即为酒驾，某研究所经实验测得，成人饮用某品牌 $38$ 度白酒后血液中酒精浓度 $y ($ 微克 $/$ 毫升 $)$ 与饮酒时间 $x ($ 小时 $)$ 之间函数关系如图所示 $($ 当 $4 \leq x \leq 10$ 时， $y$ 与 $x$ 成反比例 $)$ ．

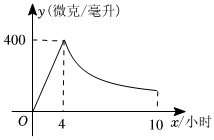(1)、根据图象直接写出：血液中酒精浓度上升阶段的函数解析式为；下降阶段的函数解析式为； $($ 并写出 $x$ 的取值范围 $)$

(2)、问血液中酒精浓度不低于 $200$ 微克 $/$ 毫升的持续时间是多少小时？

查看试题解析
19. 生活中处处充满着趣味数学，如图是河南省某海洋公园娱乐设施“水上滑梯”的侧面图，建立如图坐标系，其中 $B C$ 段可以看成是反比例函数 $y = \frac{k}{x} (x > 0)$ 图象的一段， $O D$ 为水面，矩形 $A O E B$ 为向上攀爬的梯子，每节梯子高 $0.6$ 米，宽1米．其中点A ， E ， D均在坐标轴上，且 $C D ⊥ x$ 轴．

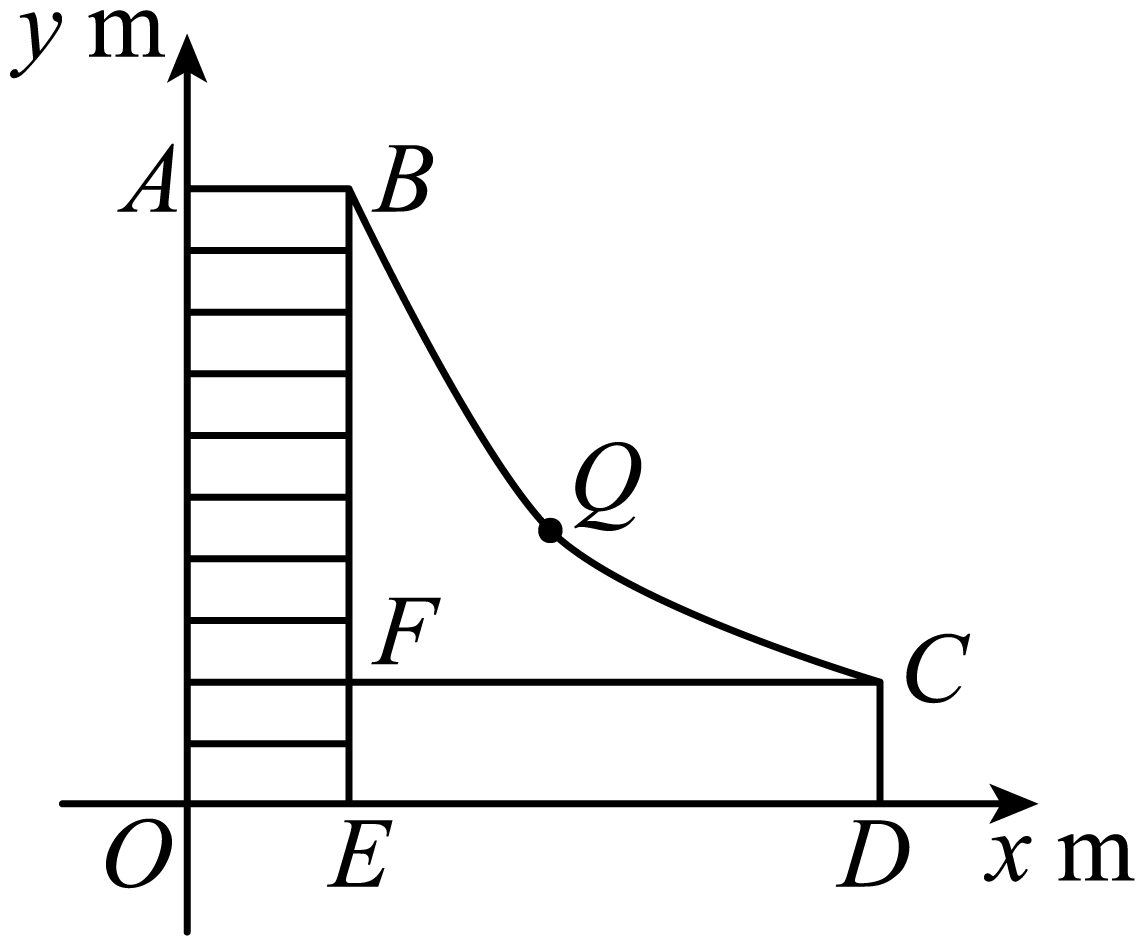(1)、求反比例函数的表达式；

(2)、求出口C点到 $B E$ 的距离 $C F$ 的长；

(3)、若滑梯 $B C$ 上有一个小球Q ，要求Q到水面的距离不高于3米，则Q到 $B E$ 的距离至少是多少米？

查看试题解析
20. 在实验课上，小明做了一个试验．如图，在仪器左边托盘 $A$ (固定)中放置一个物体，在右边托盘 $B$ (可左右移动) 中放置一个可以装水的容器，容器的质量为 $5 g$ ．在容器中加入一定质量的水，可以使仪器左右平衡．改变托盘 $B$ 与点 $C$ 的距离 $x (c m) (0 < x ⩽ 60)$ ，记录容器中加入的水的质量，得到下表：
托盘 $B$ 与点 $C$ 的距离 $x / c m$
30
25
20
15
10
容器与水的总质量 $y_{1} / g$
10
12
15
20
30
加入的水的质量 $y_{2} / g$
5
7
10
15
25
把上表中的 $x$ 与 $y_{1}$ 各组对应值作为点的坐标，在平面直角坐标系中描出这些点，并用光滑的曲线连接起来，得到如图所示的 $y_{1}$ 关于 $x$ 的函数图象．

(1)、请在该平面直角坐标系中作出 $y_{2}$ 关于 $x$ 的函数图象．

(2)、观察函数图象，并结合表中的数据：
①猜测 $y_{1}$ 与 $x$ 之间的函数关系，并求 $y_{1}$ 关于 $x$ 的函数表达式．
②求 $y_{2}$ 关于 $x$ 的函数表达式．
③当 $0 < x ⩽ 60$ 时， $y_{1}$ 随 $x$ 的增大而 ▲ (填“增大”或“减小”)， $y_{2}$ 随 $x$ 的增大而 ▲ (填“增大”或“减小”)， $y_{2}$ 的图象可以由 $y_{1}$ 的图象向 ▲ (填“上” “下”“左”或“右”)平移得到．

(3)、若在容器中加入的水的质量 $y_{2} (g)$ 满足 $19 ⩽ y_{2} ⩽ 45$ ，求托盘 $B$ 与点 $C$ 的距离 $x (c m)$ 的取值范围．

查看试题解析

$I / A$	……	5	4	$\frac{10}{3}$	$m$	2	1	0.5	0.25	……
$R / Ω$	……	20	25	30	40	50	100	200	400	……

托盘 $B$ 与点 $C$ 的距离 $x / c m$	30	25	20	15	10
容器与水的总质量 $y_{1} / g$	10	12	15	20	30
加入的水的质量 $y_{2} / g$	5	7	10	15	25

$R (Ω)$	$100$	$200$	$220$	$400$
$I (A)$	$2.2$	$1.1$		$0.55$

【提升版】北师大版数学九年级上册6.3反比例函数的应用 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学九年级上册6.3反比例函数的应用同步练习