【基础版】北师大版数学九年级上册 6.3反比例函数的应用同步练习

试卷更新日期：2024-10-10 类型：同步测试

进入出卷网下载

一、选择题

1. 在同一平面直角坐标系中，一次函数 $y_{1} = k_{1} x + b$ 与反比例函数 $y_{2} = \frac{k_{2}}{x} (x > 0)$ 的图象如图所示、则当 $y_{1} > y_{2}$ 时，自变量 $x$ 的取值范围为（）

A、 $x < 1$ B、 $x > 3$ C、 $0 < x < 1$ D、 $1 < x < 3$

查看试题解析
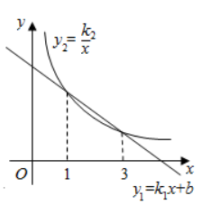2. 公元前3世纪，古希腊科学家阿基米德发现：若两物体与支点的距离与其重量成反比，则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说，已知阻力和阻力臂分别为1200N和0.5m，那么动力（）和动力臂为1.5m.

A、360N B、400N C、450N D、500N

查看试题解析
3. 古希腊著名的科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即“阻力 $\times$ 阻力臂 $=$ 动力 $\times$ 动力臂” $.$ 小明同学用撬棍撬动一块大石头，已知阻力和阻力臂分别是 $1200 N$ 和 $0.5 m$ ，则动力 $F ($ 单位： $N)$ 关于动力臂 $l ($ 单位： $m)$ 的函数表达式正确的是（）

A、 $F = \frac{1200}{l}$ B、 $F = \frac{600}{l}$ C、 $F = \frac{1000}{l}$ D、 $F = \frac{2400}{l}$

查看试题解析
4. 水果店销售某种水果，根据以往的销售经验可知：日销量 $y$ (千克)随售价 $x$ (元/千克)的变化规律符合某种函数关系．该水果店以往的售价与日销量记录如下表． $y$ 与 $x$ 的函数关系式可能是( )
售价 $x$ (元/千克)
10
15
20
25
30
日销量 $y$ (千克)
30
20
15
12
10

A、 $y = 300 x$ B、 $y = - 2 x + 50$ C、 $y = - x + 40$ D、 $y = \frac{300}{x}$

查看试题解析
5. 已知近视眼镜的度数y（度）与镜片焦距x（米）之间成反比例函数关系，如图所示，则眼镜度数y与镜片焦距x之间的函数关系式是（　　）

A、 $y = 100 x$ B、 $y = 200 x$ C、 $y = \frac{100}{x}$ D、 $y = \frac{200}{x}$

查看试题解析
6. 根据欧姆定律 $I = \frac{U}{R}$ 可知，若一个灯泡的电压 $U (V)$ 保持不变，通过灯泡的电流 $I (A)$ 越大，则灯泡就越亮 $.$ 当电阻 $R = 30 Ω$ 时，可测得某灯泡的电流 $I = 0.4 A .$ 若电压保持不变，电阻 $R$ 减小为 $15 Ω$ 时，该灯泡亮度的变化情况为( )

A、不变 B、变亮 C、变暗 D、不确定

查看试题解析
7. 2020年益阳始建高铁站，该站建设初期需要运送大量的土石方，某运输公司承担了运送总量为 $10^{6} m^{3}$ 土石方的任务，该运输公司平均运送土石方的速度 $v$ （单位： $m^{3}$ /天）与完成运送任务所需的时间 $t$ （单位：天）之间的函数关系式是（）

A、 $v = \frac{10^{6}}{t}$ B、 $v = 10^{6}$ C、 $v = \frac{1}{10^{6}} t^{2}$ D、 $v = 10^{6} t^{2}$

查看试题解析
8. 如图，直线y₁= $\frac{1}{2}$ x+2与双曲线y₂= $\frac{6}{x}$ 交于A(2，m)、B(-6，n)两点．当y₁<y₂时，x的取值范围是（）

A、x>-6或0<x<2 B、x<-6或0<x<2 C、-6<x<0或x>2 D、-6<x<2

查看试题解析

二、填空题

9. 正比例函数 $y_{1} = k_{1} x (k \neq 0)$ 与反比例函数 $y_{2} = \frac{k_{2}}{x} (k \neq 0)$ 的图象的一个交点是 $M (- 3, 2)$ ，若 $y_{2} < y_{1}$ ，则 $x$ 的取值范围是．

查看试题解析
10. 杜杆平衡时，“阻力 $\times$ 阻力臂=动力 $\times$ 动力臂”．已知阻力和阻力臂分别为 $1600 N$ 和 $0.5 m$ ，动力为 $F (N)$ ，动力臂为 $l (m)$ ．则动力 $F$ 关于动力臂 $l$ 的函数表达式为．

查看试题解析
11. 在平面直角坐标系中，函数 $y = \frac{2}{x} (x > 0)$ 与 $y = x - 1$ 的图象交于点 $P (a ， b)$ ，则代数式 $a - b + a b$ 的值为.

查看试题解析
12. 一个游泳池的容积为 $2000 m^{3}$ ，游泳池注满水所用时间 $t$ 与注水速度 $v$ （填“成正比例”、“成反比例”、“不成比例”）．

查看试题解析
13. 验光师通过检测发现近视眼镜的度数 $y ($ 度 $)$ 与镜片焦距 $x ($ 米 $)$ 成反比例， $y$ 关于 $x$ 的函数图象如图所示 $.$ 经过一段时间的矫正治疗后，小雪的镜片焦距由 $0.25$ 米调整到 $0.5$ 米，则近视眼镜的度数减少了度

查看试题解析

三、解答题

14. 周末，学校组织全体团员进行社会实践活动，活动结束后，李杰要把一份1600字的社会调查报告录入电脑.设他录入文字的速度为 $v$ 字/分，完成录入所需的时间为 $t$ 分钟.

(1)、求 $t$ 与 $v$ 之间的函数关系式；

(2)、当李杰录入文字的速度 $v$ 为100字/分，完成录入的时间 $t$ 为多少？

查看试题解析
15. 如图，一次函数y=kx+b的图象经过第一、二、三象限，且与反比例函数图象相交于A，B两点，与x轴交于点D，OB= $\sqrt{5}$ ，且点B的横坐标是点B的纵坐标的2倍．

(1)、求反比例函数的解析式．

(2)、如图，一次函数y=kx+b的图象向下平移10个单位长度，得到新的函数图象与x轴交于点C．设点A的横坐标为m，若△ABC的面积S=15，求m的值．

查看试题解析
16. 设每名工人一天能做某种型号的工艺品 $x$ 个．若某工艺品厂每天要生产这种工艺品 $60$ 个，则需工人 $y$ 名．

(1)、求 $y$ 关于 $x$ 的函数表达式．

(2)、若一名工人每天能做的工艺品个数最少 $6$ 个，最多 $8$ 个，估计该工艺品厂每天需要做这种工艺品的工人多少人．

查看试题解析
17. 石阡是“中国苔茶之乡”，是茶树的原产地之一，有千年的茶叶栽种历史．某次茶艺比赛中指定使用的饮水机4分钟就可以将 $20 ℃$ 的饮用水加热到 $100 ℃$ ．此后停止加热，水温开始下降．如图所示，已知整个下降过程中水温 $y (℃)$ 与通电时间 $x (m i n)$ 成反比例关系．

(1)、在水温下降过程中，求y与x的函数解析式；

(2)、比赛组织方要求，参赛选手必须把组织方提供的 $20 ℃$ 的饮用水用该款饮水机加热到 $100 ℃$ ，然后降温到 $80 ℃$ 方可使用．求从饮水机加热开始，到可以使用需要等待多长时间？

查看试题解析
18. 某一菩水池中有水若干吨，若单一个出水口，排水速度 $v (m^{3} / h)$ 与排完蓄水池中的水所用的时间 $t (h)$ 之间的对应关系如下表：
排水速度 $v (m^{3} / h)$
1
2
3
4
6
8
12
所用的时间 $t (h)$
12
6
4
3
2
1.5
1

(1)、在如图的直角坐标系中，用描点法画出相应函数的图象．

(2)、写出 $t$ 与 $v$ 之间的函数关系式．

(3)、若 $5 h$ 排完蓄水池中的水，那么每小时的排水量至少应该是多少？

查看试题解析
19. 某学校准备修建一个面积为 $100 m^{2}$ 的矩形花圃，设矩形花圃的一边长为 $x m$ ，相邻的另一边长为 $y m$ ．

(1)、求y关于x的函数表达式；

(2)、若矩形的一边长x满足 $x > 50$ ，求另一边长y的取值范围；

(3)、杭杭在实践后得到如下结论：在面积为 $100 m^{2}$ 的情况下，不存在周长为 $30 m$ 的矩形．请判断他的说法是否正确，并说明理由．

查看试题解析
20. 如图，在左边托盘A（固定）中放置一个重物，在右边托盘B（可左右移动）中放置一定质量的砝码，可使得仪器左右平衡．托盘B中的砝码质量m随着托盘B与点O的距离d变化而变化，已知m与d是反比例函数关系，下面是它们的部分对应值：
托盘B与点O的距离d/厘米
5
10
15
20
25
托盘B中的砝码质量m/克
30
15
10
$7.5$
6

(1)、根据表格数据求出m关于d的函数解析式．

(2)、当砝码质量为12克时，求托盘B与点O的距离．

查看试题解析

售价 $x$ (元/千克)	10	15	20	25	30
日销量 $y$ (千克)	30	20	15	12	10

排水速度 $v (m^{3} / h)$	1	2	3	4	6	8	12
所用的时间 $t (h)$	12	6	4	3	2	1.5	1

托盘B与点O的距离d/厘米	5	10	15	20	25
托盘B中的砝码质量m/克	30	15	10	$7.5$	6

【基础版】北师大版数学九年级上册 6.3反比例函数的应用 同步练习

一、选择题

二、填空题

三、解答题

【基础版】北师大版数学九年级上册 6.3反比例函数的应用同步练习