【培优版】北师大版数学九年级上册6.2反比例函数的图象与性质 同步练习
试卷更新日期:2024-10-09 类型:同步测试
一、选择题
-
1. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则2. 如图 , 点、在反比例函数的图象上,过点、作轴的垂线,垂足分别为 , , 延长线段交轴于点 , 当时,阴影部分的面积;如图 , 点、在反比例函数的图象上,过点、作轴的垂线,垂足分别为 , , 连接 , 交于于点 , 当时,阴影部分的面积 , 则的值为( )
 A、 B、 C、 D、3. 如图,在反比例函数的图像上,有点 , , , , 它们的横坐标依次为1,2,3,4.分别过这些点作垂直于x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为 , , , 若 , 则的值为( )
A、 B、 C、 D、3. 如图,在反比例函数的图像上,有点 , , , , 它们的横坐标依次为1,2,3,4.分别过这些点作垂直于x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为 , , , 若 , 则的值为( ) A、2.5 B、3 C、4 D、无法确定4. 如图,已知点A(3,0),B(0,4),C是y轴上位于点B上方的一点,AD平分∠OAB,BE平分∠ABC,直线BE交AD于点D.若反比例函数y=(x<0)的图象经过点D,则k的值是( )
A、2.5 B、3 C、4 D、无法确定4. 如图,已知点A(3,0),B(0,4),C是y轴上位于点B上方的一点,AD平分∠OAB,BE平分∠ABC,直线BE交AD于点D.若反比例函数y=(x<0)的图象经过点D,则k的值是( ) A、-8 B、-9 C、-10 D、-125. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( )
A、-8 B、-9 C、-10 D、-125. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( ) A、-8 B、-6 C、-4 D、-26. 如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( )
A、-8 B、-6 C、-4 D、-26. 如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( ) A、-2 B、-4 C、-6 D、-87. 如图, 的边 在x轴上,边 交y轴于点E, ,反比例函数 过C点,且交线段 于D, ,连接 ,若 ,则k的值为( )
A、-2 B、-4 C、-6 D、-87. 如图, 的边 在x轴上,边 交y轴于点E, ,反比例函数 过C点,且交线段 于D, ,连接 ,若 ,则k的值为( ) A、 B、 C、4 D、68. 如图,点A、M是第一象限内双曲线 (k为常数, , )上的点(点M在点A的左侧),若M点的纵坐标为1,且△OAM为等边三角形,则k的值为( )
A、 B、 C、4 D、68. 如图,点A、M是第一象限内双曲线 (k为常数, , )上的点(点M在点A的左侧),若M点的纵坐标为1,且△OAM为等边三角形,则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,反比例函数的图象经过矩形对角线的交点 , 分别交 , 于点、 . 若四边形的面积为12,则的值为 .
 10. 如图,点在反比例函数()的图象上,且点是线段的中点,点为轴上一点,连接交反比例函数图象于点 , 连接 , 若 , , 则的值为 .
10. 如图,点在反比例函数()的图象上,且点是线段的中点,点为轴上一点,连接交反比例函数图象于点 , 连接 , 若 , , 则的值为 . 11. 如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C . 交AB于点D , 连结CD . 若△ACD的面积是2,则k的值是 .
11. 如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C . 交AB于点D , 连结CD . 若△ACD的面积是2,则k的值是 . 12. 如图,已知等边 , 顶点在双曲线上,点的坐标为 . 过作交双曲线于点 , 过作交轴于点 , 得到第二个等边;过作交双曲线于点 , 过作交轴于点 , 得到第三个等边;以此类推,…,则点的坐标为 .
12. 如图,已知等边 , 顶点在双曲线上,点的坐标为 . 过作交双曲线于点 , 过作交轴于点 , 得到第二个等边;过作交双曲线于点 , 过作交轴于点 , 得到第三个等边;以此类推,…,则点的坐标为 . 13. 如图,在矩形AOBC中,OB=8,OA=6,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 (k>0)的图象与AC边交于点E,将△CEF沿EF对折后,C点恰好落在OB上的点D处,则k的值为.
13. 如图,在矩形AOBC中,OB=8,OA=6,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 (k>0)的图象与AC边交于点E,将△CEF沿EF对折后,C点恰好落在OB上的点D处,则k的值为.
三、解答题
-
14. 如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作为的整数).反比例函数的图象为曲线 .
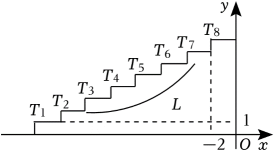 (1)、若过点 , 求反比例函数的解析式;(2)、若过点 , 则它必定还过另一点 , 求的坐标;(3)、若曲线使得这些点分布在它的两侧,每侧各4个点,求出所有满足条件的整数 .15. 综合与探究
(1)、若过点 , 求反比例函数的解析式;(2)、若过点 , 则它必定还过另一点 , 求的坐标;(3)、若曲线使得这些点分布在它的两侧,每侧各4个点,求出所有满足条件的整数 .15. 综合与探究如图1,反比例函数的图象经过点A,点A的横坐标是-2,点A关于坐标原点O的对称点为点B,作直线 .
 (1)、判断点B是否在反比例函数的图象上,并说明理由;(2)、如图1,过坐标原点O作直线交反比例函数的图象于点C和点D,点C的横坐标是4,顺次连接 , , 和 . 求证:四边形是矩形;(3)、已知点P在x轴的正半轴上运动,点Q在平面内运动,当以点O,B,P和Q为顶点的四边形为菱形时,请直接写出此时点P的坐标.16. 如图,在平面直角坐标系中,、是矩形的两个顶点,点D是线段上的一个动点(不与重合),双曲线()经过点D,与矩形的边相交于点E.
(1)、判断点B是否在反比例函数的图象上,并说明理由;(2)、如图1,过坐标原点O作直线交反比例函数的图象于点C和点D,点C的横坐标是4,顺次连接 , , 和 . 求证:四边形是矩形;(3)、已知点P在x轴的正半轴上运动,点Q在平面内运动,当以点O,B,P和Q为顶点的四边形为菱形时,请直接写出此时点P的坐标.16. 如图,在平面直角坐标系中,、是矩形的两个顶点,点D是线段上的一个动点(不与重合),双曲线()经过点D,与矩形的边相交于点E.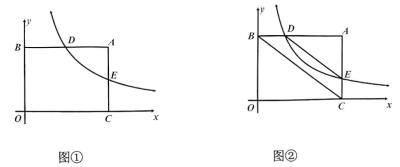
 (1)、如图①,当点D为中点时,k的值为 , 点E的坐标为;(2)、如图②,当点D在线段上的任意位置时(不与重合),连接 , 求证:;(3)、是否存在反比例函数上不同于点D的一点F,满足:为直角三角形, , 且 , 若存在,请直接写出满足以上条件时点D的横坐标,若不存在,请说明理由.17. 阅读理解:
(1)、如图①,当点D为中点时,k的值为 , 点E的坐标为;(2)、如图②,当点D在线段上的任意位置时(不与重合),连接 , 求证:;(3)、是否存在反比例函数上不同于点D的一点F,满足:为直角三角形, , 且 , 若存在,请直接写出满足以上条件时点D的横坐标,若不存在,请说明理由.17. 阅读理解:材料一:若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三数组”.
材料二:若关于x的一元二次方程ax2+bx +c= 0(a≠0)的两根分别为 , ,则有 , .
问题解决:
(1)、请你写出三个能构成“和谐三数组”的实数;(2)、若 , 是关于x的方程ax2+bx +c= 0 (a,b,c均不为0)的两根, 是关于x的方程bx+c=0(b,c均不为0)的解.求证:x1 , x2 , x3可以构成“和谐三数组”;(3)、若A(m,y1) ,B(m + 1,y2) ,C(m+3,y3)三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成“和谐三数组”,求实数m的值.18. (1)、【感知】如图1,已知反比例函数上有两点 , , 轴交轴于点 , 轴交轴于点 , 则 , , 与的位置关系为: .(2)、【探究】我们对上述问题进行了思考,如图2,当 , 是双曲线同一支上任意两点,过、分别向轴、轴作垂线,交轴于点 , 交轴于点 , 连接、 .
(1)、【感知】如图1,已知反比例函数上有两点 , , 轴交轴于点 , 轴交轴于点 , 则 , , 与的位置关系为: .(2)、【探究】我们对上述问题进行了思考,如图2,当 , 是双曲线同一支上任意两点,过、分别向轴、轴作垂线,交轴于点 , 交轴于点 , 连接、 .①试探究与面积的关系并说明理由;
②试探究与之间的位置关系并说明理由.
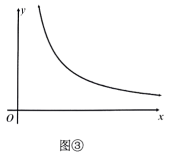
(3)、【运用】我们对上述问题进行了实践,如图3,已知点 , 在反比例函数的图像上,且 , 则是反比例函数第三象限内图像上的一动点,过点作轴,过点作轴,垂足分别分为、 , 若四边形的面积为45,求点的坐标;(4)、【拓展】我们对上述问题进行了延伸,如图4,函数的图像与过原点的直线相交于 , 两点,点是此函数第二象限内图像上的动点(点在点的右侧),直线分别交于轴、轴于点、 , 连接分别交轴、轴于点、 . 若 , 求的值?