【提升版】北师大版数学九年级上册6.2反比例函数的图象与性质同步练习

试卷更新日期：2024-10-09 类型：同步测试

进入出卷网下载

一、选择题

1. 反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象如图所示，则k的值可能是（　　）

A、5 B、12 C、-5 D、-12

查看试题解析
2. 如图直线y＝mx与双曲线y= $\frac{k}{x}$ 交于点A、B ，过A作AM⊥x轴于M点，连接BM ，若S_△_AMB＝2，则k的值是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 若点 $A (- 4, a)$ ， $B (1, b)$ ， $C (2, c)$ 都在反比例 $y = \frac{4}{x}$ 的图象上，则 $a$ ， $b$ ， $c$ 大小关系正确的是（）

A、 $a < b < c$ B、 $a < c < b$ C、 $b < c < a$ D、 $c < b < a$

查看试题解析
4. 在函数 $y = \frac{- m^{2} - 3}{x - 1}$ （ $m$ 为常数）的图象上有三点 $(- 4, y_{1}), (- 2, y_{2}), (1, y_{3})$ ，则函数值 $y_{1}, y_{2}, y_{3}$ 的大小关系为（）

A、 $y_{2} < y_{1} < y_{3}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
5. 当k＜0时，反比例函数 $y = \frac{k}{x}$ 和一次函数y＝kx＋2的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 得天独厚的自然条件和生态资源，已让铜仁这片黔东沃土孕育出33个地理标志产品．在2023梵净山国际地理标志研讨会议召开之际，某区举行地理标志产品知识竞赛，如图使用 $S_{矩形 A B C O}$ 、 $S_{矩形 D E F O}$ 、 $S_{矩形 G H I O}$ 、 $S_{矩形 J K L O}$ 分别描述了甲、乙、丙、丁四个社区居民竞赛成绩的优秀人数，已知y表示社区居民竞赛成绩的优秀率，x表示该社区参赛居民人数，占B和点K在同一条反比例函数图象上，则这四个社区在这次知识竞赛中优秀人数最多的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 如图，直线AB交x轴于点C，交反比例函数y＝ $\frac{a - 1}{x}$ （a＞1）的图像于A、B两点，过点B作BD⊥y轴，垂足为点D，若S_△BCD＝5，则a的值为（）

A、8 B、9 C、10 D、11

查看试题解析
8. 点 $(2 ， - 3)$ 在函数 $y = \frac{k}{x}$ 图象上，下列说法中错误的是（）

A、它的图象分布在二、四象限 B、当 $x > 0$ 时，y的值随x的增大而增大 C、当 $x < 0$ 时，y的值随x的增大而减小 D、它的图象过点 $(- 1 ， 6)$

查看试题解析

二、填空题

9. 如图，点M是反比例函数y＝ $\frac{a}{x}$ （a≠0）的图象上一点，过M点作x轴、y轴的平行线，若S_阴影=8，则此反比例函数解析式为

查看试题解析
10. 如图，双曲线 $y = \frac{k}{x} (x > 0)$ 经过 $△ A B C$ 的两顶点A、C， $A B ∥ x$ 轴交y轴于点B，过点C作 $C D ⊥ y$ 轴于点D，若 $O B = C D = 2$ ，且 $△ A B C$ 的面积为4，则k的值为．

查看试题解析
11. 如图，矩形ABCD的边AB与y轴平行，顶点B的坐标为（1，m），D（5，m＋2），反比例函数 $y = \frac{k}{x}$ （x>0）的图象同时经过点A与点C，则k的值为．

查看试题解析
12. 如图，已知点A、B分别在反比例函数y＝﹣ $\frac{3}{x}$ （x＜0）与y＝ $\frac{6}{x}$ （x＞0）图象上，且OA⊥OB ，若AB＝6，则△AOB的面积为．

查看试题解析
13. 如图，正方形的顶点 $A ， C$ 分别在 $y$ 轴和 $x$ 轴上，边 $B C$ 的中点 $F$ 在 $y$ 轴上，若反比例函数 $y = \frac{12}{x}$ 的图象恰好经过 $C D$ 的中点 $E$ ，则 $O A$ 的长为．

查看试题解析

三、解答题

14. 已知反比例函数 $y = \frac{k - 4}{x}$ 的图象经过第一、三象限．

(1)、求 $k$ 的取值范围；

(2)、若 $a > 0$ ，此函数的图象过第一象限的两点 $(a + 5 ， y_{1}) (2 a + 1 ， y_{2})$ ，且 $y_{1} < y_{2}$ ，求 $a$ 的取值范围．

查看试题解析
15. 如图，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像分别交正方形 $O A B C$ 的边 $A B 、 B C$ 于点 $D$ 、 $E$ ，若 $A$ 点坐标为 $(1 ， 0)$ ，若 $△ O D E$ 是等边三角形，求 $k$ 的值.

查看试题解析
16. 如图，点A、B分别在反比例函数 $y_{1} = \frac{k_{1}}{x} (x > 0)$ 和 $y_{2} = \frac{k_{2}}{x} (x > 0)$ 的图象上，线段AB与x轴相交于点P．

(1)、如图①，若AB⊥x轴，且|AP|＝2|PB|，k₁+k₂＝1．求k₁、k₂的值；

(2)、如图②，若点P是线段AB的中点，且△OAB的面积为2．求k₁-k₂的值．

查看试题解析
17. 如图，点A在反比例函数 $y = \frac{m}{x} (m > 0 ， x > 0)$ 的图像上，点A的纵坐标为3.过点A作x轴的平行线交反比例函数 $y = \frac{n}{x} (n > m ， x > 0)$ 的图像于点C.点P为线段AC上一动点，过点P作 $A C$ 的垂线，分别交反比例函数 $y = \frac{m}{x}$ 和 $y = \frac{n}{x}$ 的图像于点B，D.

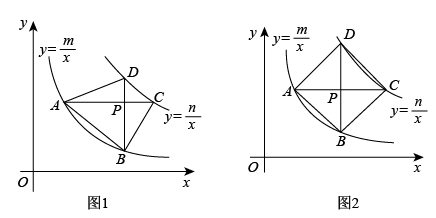(1)、当 $m = 4 ， n = 16$ 时，
①若点P的横坐标为4（如图1），求直线 $A B$ 的函数表达式；
②若点P是 $A C$ 的中点（如图2），试判断四边形 $A B C D$ 的形状，并说明理由；

(2)、四边形 $A B C D$ 能否成为正方形？若能，求此时m，n之间的数量关系；若不能，说明理由.

查看试题解析
18. 阅读理解：
如图（1），在平面直角坐标系xOy中，已知点A的坐标是（1，2），点B的坐标是（3，4），过点A、点B作平行于x轴、y轴的直线相交于点C，得到Rt△ABC，由勾股定理可得，线段AB＝ $\sqrt{A C^{2} + B C^{2}} = \sqrt{{(3 - 1)}^{2} + {(4 - 2)}^{2}} = 2 \sqrt{2}$ .

得出结论：

(1)、若A点的坐标为（x₁ ， y₁），B点的坐标为（x₂ ， y₂）请你直接用A、B两点的坐标表示A、B两点间的距离；
应用结论：

(2)、若点P在y轴上运动，试求当PA＝PB时，点P的坐标.

(3)、如图（2）若双曲线L₁：y＝ $\frac{k}{x}$ （x＞0）经过A（1，2）点，将线段OA绕点O旋转，使点A恰好落在双曲线L₂：y＝﹣ $\frac{k}{x}$ （x＞0）上的点D处，试求A、D两点间的距离.

查看试题解析

【提升版】北师大版数学九年级上册6.2反比例函数的图象与性质 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学九年级上册6.2反比例函数的图象与性质同步练习