人教版数学八年级上学期第一次质量检测进阶测试

试卷更新日期：2024-10-09 类型：月考试卷

进入 出卷网 下载

一、选择题（每题3分，共30分）

  • 1. 下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（       ）
    A、2cm ， 3cm ， 1cm B、2cm ， 2cm ， 6cm C、5cm ， 10cm ， 4cm D、7cm ， 5cm ， 10cm

    查看试题解析

  • 2. 如图，△ABC≌△DEC ， B、C、D在同一直线上，且CE=6 ， AC=8 ， 则BD长（       ）

    A、12 B、14 C、16 D、18

    查看试题解析

  • 3. 如图，将△ABC纸片沿DE折叠，使点A落在四边形BCED内点A'的位置∠A=35° ， 则∠1+∠2的度数是（     ）

    A、80° B、70° C、45° D、35°

    查看试题解析

  • 4. 已知直角三角形30°角所对的直角边长为5，则斜边的长为（ ）
    A、5 B、10 C、8 D、12

    查看试题解析

  • 5. 如图，OC平分∠AOB，OD平分∠AOC，∠AOD=40°，则∠AOB的度数是（ ）

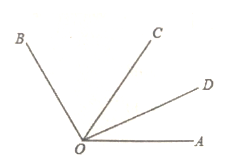    A、160° B、120° C、80° D、60°

    查看试题解析

二、填空题（每题3分，共24分）

  • 6. 如图， ΔABC 中， ∠ACB=90∘ ， AC<BC ，将 ΔABC 沿 EF 折叠，使点 A 落在直角边 BC 上的 D 点处，设 EF 与 AB、AC 边分别交于点 E、F ，如果折叠后 ΔCDF 与 ΔBDE 均为等腰三角形，那么 ∠B= .

    查看试题解析

  • 7. 如图，△ABC中∠BAC=60° ， 将△ACD沿AD折叠，使得点C落在AB上的点C'处，连接C'D与C'C ， ∠ACB的角平分线交AD于点E；如果BC'=DC'；那么下列结论：①∠1=∠2；②AD垂直平分C'C；③∠B=3∠BCC'；④DC'∥EC；其中正确的是：；（只填写序号）

    查看试题解析

  • 8. 如图，△ABC的周长为12，OB、OC分别平分∠ABC和∠ACB，过点O作OD⊥BC于点D，OD=3，则△ABC的面积为.

    查看试题解析

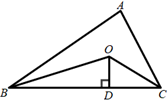  • 9. 如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB'C'．若点B'恰好落在BC边上，且AB'＝CB'，则∠C'的度数为 ．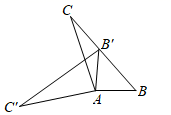

    查看试题解析

三、证明题（共8题）

  • 10. 如图，在Rt△ABC中，∠B=90°，点E是AC的中点，AC=2AB，∠BAC的平分线AD交BC于点D，作AF∥BC，连接DE并延长交AF于点F，连接FC．求证：AF=DA．

    查看试题解析

四、作图题（共10分）

  • 11. 如图，在规格为8×8的边长为1个单位的正方形网格中（每个小正方形的边长为1），△ABC的三个顶点都在格点上，且直线m、n互相垂直．

    (1)、画出△ABC关于直线n对称的△A'B'C'；
    (2)、在直线m上作出点P ， 使得△APB的周长最小.（保留作图痕迹）

    查看试题解析

五、解答题（共2题，共32分）

  • 12. 如图，已知B(−1 ， 0) ， C(1 ， 0) ， A为y轴正半轴上一点，点D为第二象限一动点，E在BD的延长线上，CD交AB于F ， 且∠BDC=2∠BAO ．

    (1)、求证：∠ABD=∠ACD；
    (2)、求证：AD平分∠CDE；
    (3)、若在D点运动的过程中，始终有DC=DA+DB在此过程中，∠BAC的度数是否变化?如果变化，请说明理由；如果不变，请求出∠BAC的度数．

    查看试题解析

六、实践探究题（共16分）

  • 13. 在直线m上依次取互不重合的三个点D ， A ， E ， 在直线m上方有AB=AC ， 且满足∠BDA=∠AEC=∠BAC=α ．
    (1)、【积累经验】

    如图1，当α=90°时，猜想线段DE ， BD ， CE之间的数量关系是；

    (2)、【类比迁移】

    如将2，当0<α<180°时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；

    (3)、【拓展应用】

    如图3，在△ABC中，∠BAC是钝角，AB=AC ， ∠BAD<∠CAE ， ∠BDA=∠AEC=∠BAC ， 直线m与CB的延长线交于点F ， 若BC=3FB ， △ABC的面积是12，请直接写出△FBD与△ACE的面积之和．

    查看试题解析