浙教版（2024）数学七年级上册《第6章 图形的初步知识》单元提升测试卷
试卷更新日期：2024-10-03 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 观察图形，下列有四种说法：①经过一点可以作无数条直线；②射线和射线是同一条射线；③三条直线两两相交，有3个交点；④ ． 其中正确的个数为（ ）
A、1 B、2 C、3 D、42.如图，下列表示角的方法，错误的是（ ）
A、∠1与∠AOB表示同一个角 B、∠AOC也可用∠O来表示 C、图中共有三个角：∠AOB、∠AOC、∠BOC D、∠β表示的是∠BOC3. 已知线段 ， 延长至点 ， 使 ， 点 ， 分别为线段 ， 的中点，则的长度为（ ）A、2cm B、3cm C、5cm D、1cm或5cm4. 已知线段 ， 点C为线段AB的中点，点D为线段AC上的三等分点，则线段BD的长的最大值为（ ）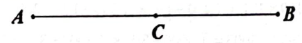
A、16 B、18 C、15 D、205. 下列说法正确的个数是（ ）①连接两点之间的线段叫两点间的距离
②射线有两个端点
③若AB＝2CB，则点C是AB的中点
④若∠A＝20°18′，∠B＝20°28″，∠C＝20.25°，则有∠A＞∠C＞∠B
A、1个 B、2个 C、3个 D、4个6. 如图，将一副三角板叠在一起使直角顶点重合于点O，（两块三角板可以在同一平面内自由转动），下列结论一定成立的是（ ）
A、∠BOA＞∠DOC B、∠BOA﹣∠DOC＝90° C、∠BOA+∠DOC＝180° D、∠BOC≠∠DOA7. 如图，直线AB、CD交于点O，OE平分∠BOC，若∠1＝36°，则∠DOE等于（ ）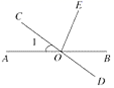
A、73° B、90° C、107° D、108°8.将矩形ABCD沿AE折叠，得到如图图形．若∠CED′=56°，则∠AED的大小是（ ）
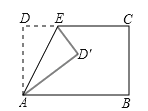A、56° B、60° C、62° D、65°9. 定义：从的顶点出发，在角的内部引一条射线 ， 把分成：的两部分，射线叫做的三等分线若在中，射线是的三等分线，射线是的三等分线，设 ， 则用含的代数式表示为（ ）A、或或 B、或或 C、或或 D、或或10. 如图， ， 平分 ， 平分 ， 若 ， 则的度数是（ ）
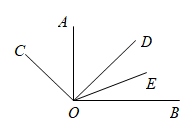A、 B、 C、 D、二、填空题（每题3分，共18分）
-
11. 如图，O是直线上的点，是的平分线，若 ， 则 ．
12. 一个角的补角比这个角的余角的4倍少60°，这个角的度数是（度）．13. 线段 ， C为线段AB的中点，点D在直线AB上，若 ， 则CD＝ ．14. 一副三角板按如图方式摆放，且 的度数比 的度数小 ，则 的度数为 .
15. 如图，点O在直线AB上，从点O引出射线OC，其中射线OD平分∠AOC，射线OE平分∠BOC，下列结论：
①∠DOE＝90°；
②∠COE与∠AOE互补；
③若OC平分∠BOD，别∠AOE＝150°；
④∠BOE的余角可表示为 ．
其中正确的是 ． （只填序号）
16. 如图所示：已知 ， ，现有 点和 点分别从 ， 两点出发相向运动， 点速度为 ， 点速度为 ，当 到达 点后掉头向 点运动， 点在向 的运动过程中经过 点时，速度变为 ， ， 两点中有一点到达 点时，全部停止运动，那么经过 后 的距离为 ．
三、解答题（共8题，共72分）
-
17. 如图，线段 ， C是线段AB的中点，D是线段BC的中点.
(1)、求线段AD的长；(2)、在线段AD上有一点E ， 满足 ， 求AE的长.18. 如图，已知点在线段的延长线上，点 ， 分别是 ， 的中点．
(1)、若 ， ， 则线段； ． （直接写出结果）(2)、若 ， ， 其他条件不变，求线段的长．（用含的式子表示）19. 已知：两块三角尺（直角三角形和直角三角形）按如图1摆放，点在同一条直线上，分别平分和 ．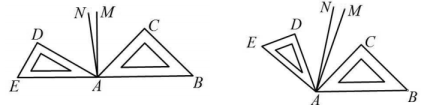
图1 图2
(1)、求的度数；(2)、求的度数；(3)、将三角尺绕点按顺时针方向转动至如图2的位置，在转动过程中，的度数是否发生变化？如果不变化，请求出的度数；如果变化，请说明理由．20. 如图，点O是数轴的原点，点A在数轴上位于原点左侧，点B在数轴上位于原点右侧， ．
(1)、当 ， 时，点A表示的数为 ， 点B表示的数为；(2)、若点C、D为数轴上任意两点，点M是线段AC的中点，点N是线段BD的中点．①当点C与点D重合时，探究AB与MN的数量关系，并说明理由．
②当时，直接写出MN的长度（用m ， n表示）．
21. 如图1，点O为直线AB上一点，过O点作射线OC，使∠AOC：∠BOC＝1：2，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．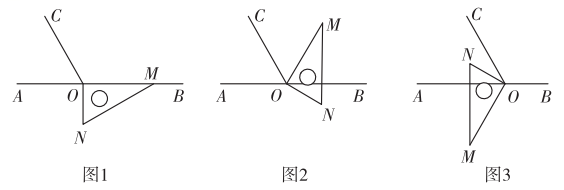
(1)、如图2，将图1中的三角板绕点O逆时针方向旋转60°至图2的位置，求∠MOC的度数；(2)、如图3，将图1中的三角板绕点O按每秒10°的速度逆时针方向旋转α度（0<α<360°）．①若经过t秒后线段ON在∠AOC的内部，且∠AOM＝3∠NOC，求t的值；
②在三角板转动时，射线OC同时绕点O以每秒4°的速度按顺时针方向旋转，当三角板停止转动时，射线OC也停止转动．经过t秒直线ON恰好平分∠AOC，请直接写出满足条件的t的值．
22. 已知 ， 射线在的内部， ． 将射线绕点逆时针旋转形成射线 ．
(1)、如图1，若 ， 那么和的度数相等吗？为什么？(2)、作射线 ， 使射线为的平分线．①如图2，当射线恰好平分时，求的度数；
②如图3，设 ， 试探究与之间有何数量关系？说明理由．
23. 定义：若线段上的一个点把这条线段分成的两条线段，则称这个点是这条线段的三等分点．
图1 图2
(1)、如图1，点是线段的一个三等分点，满足 ， 若 ， 则 ．(2)、如图2，已知 ， 点从点出发，点从点出发，两点同时出发，都以每秒的速度沿射线方向运动秒．①当为何值时，点是线段的三等分点．
②在点 ， 点开始出发的同时，点也从点出发，以每秒的速度沿射线方向运动，在运动过程中，点 ， 点分别是 ， 的三等分点，请直接写出的值．
24.
(1)、如图1，已知点M ， N是线段CD上两点，且 ， 点E和点F分别是线段CN和线段DM的中点．若线段 ， 分别求线段 ， ， 的长；(2)、已知OM ， ON是从的顶点发出的两条射线，且 ， 射线OE和射线OF分别平分 ， ．①如图2，若OM ， ON均为内的两条射线，且 ， 求的度数；
②如图3，若OM为外的一条射线，且 ， 则 ▲ ．