【培优版】北师大版数学九年级上册5.1投影 同步练习
试卷更新日期：2024-10-02 类型：同步测试
一、选择题
-
1.
如图，一天晚上，小颖由路灯A下的B处走到C处时，测得影子CD的长为1米，当她继续往前走到D处时，测得此时影子DE的长刚好是自己的身高，已知小颖的身高为1.5米，那么路灯A的高度AB为（ ）
A、3米 B、4.5米 C、6米 D、8米2.如图，AB， CD是两根木杆，它们在同一平面内的同一直线MN上，则下列有关叙述正确的是（ ）
A、若射线BN正上方有一盏路灯，则AB，CD的影子都在射线BN上 B、若线段BD正上方有一盏路灯，则AB的影子在射线BM上，CD的影子在射线DN上 C、若在射线DN正上方有一盏路灯，则AB，CD的影子都在射线BN上 D、若太阳处在线段BD的正上方，则AB， CD的影子位置与选项B中相同.3. 小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况，无意之中，他发现这四个时刻向日葵影子的长度各不相同，那么影子最长的时刻为（ ）A、上午12时 B、上午10时 C、上午9时30分 D、上午8时4. 太阳光线与地面成60°的角，照射在地面上的一只皮球上，皮球在地面上的投影长是 ，则皮球的直径是（ ）
A、 B、15 C、10 D、5. 如图所示，平地上一棵树高为6米，两次观察地面上的影子，第一次是当阳光与地面成60°时，第二次是阳光与地面成30°时，第二次观察到的影子比第一次长（ ）
A、 B、 C、 D、6. 如图，晚上小亮在路灯下经过，在小亮由A处径直走到B处这一过程中，他在地上的影子（ ）
A、逐渐变短 B、先变短后变长 C、逐渐变长 D、先变长后变短7. 圆桌面（桌面中间有一个直径为0.4m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为1.2m，桌面离地面1m，若灯泡离地面3m，则地面圆环形阴影的面积是（ ）
A、0.324πm2 B、0.288πm2 C、1.08πm2 D、0.72πm28. 如图中三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄的，则按时间先后顺序可排列为（ ）
A、③②① B、②①③ C、①②③ D、②③①二、填空题
-
9. 小莉身高 ，在阳光下的影子长为 ，在同一时刻站在阳光下，小林的影长比小莉长 ，则小林的身高为 ．10. 如图，在平面直角坐标系中，点光源位于处，木杆两端的坐标分别为 ， 则木杆在轴上的影长为 ．
11. 如图，小明站在距地面5.1m的路灯OP下点A处，此时他的影长 ，小明沿直线向前走了2m到达了点B处，此时他的影长 ，则小明的身高为m.
12. 《孙子算经》是我国古代重要的数学著作，成书于约一千五百年前，其中有道歌谣算题：“今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问杆长几何？”歌谣的意思是：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五，同时立一根一尺五的小标杆，它的影长五寸（提示：仗和尺是古代的长度单位，1丈＝10尺，1尺＝10寸），可以求出竹竿的长为尺．13. 如图，当太阳在A处时，小明测得某树的影长为2米，当太阳在B处时又测得该树的影长为8米．若两次日照的光线互相垂直，则这棵树的高度为米．
三、解答题
-
14. 如图，某墙壁左侧有一木杆和一棵松树.某一时刻在太阳光下，木杆的影子刚好不落在墙壁上，已知 ， .
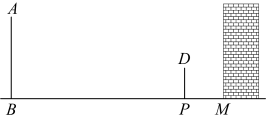(1)、请画出在同一时刻下松树AB在阳光下的投影；(2)、若木杆 ， 木杆DP的投影 ， 同一时刻松树AB在阳光下的投影 ， 求松树的高度.15. 如图，公路旁有两个高度相等的路灯AB、CD，小明上午上学时发现路灯AB在太阳光下的影子恰好落在路牌底部E处，他自己的影子恰好落在路灯CD的底部C处；晚自习放学时，站在上午同一个地方，发现在路灯CD的灯光下自己的影子恰好落在E处．
(1)、在图中画出小明的位置(用线段FG表示)．(2)、若上午上学时，高1米的木棒的影子为2米，小明身高为1.5米，他距离路牌底部E恰好2米，求路灯高．16. 【综合与实践】现实生活中，人们可以借助光源来测量物体的高度．已知榕树CD，FG和灯柱AB如图①所示，在灯柱AB上有一盏路灯P，榕树和灯柱的底端在同一水平线上，两棵榕树在路灯下都有影子，只要测量出其中一些数据，则可求出所需要的数据，具体操作步骤如下：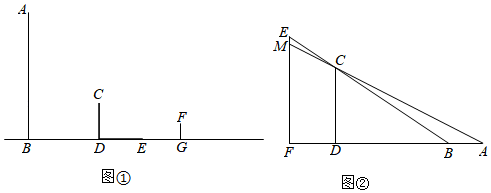
①根据光源确定榕树在地面上的影子；
②测量出相关数据，如高度，影长等；
③利用相似三角形的相关知识，可求出所需要的数据．
根据上述内容，解答下列问题：
(1)、已知榕树CD在路灯下的影子为DE，请画出榕树FG在路灯下的影子GH；(2)、如图①，若榕树CD的高度为3.6米，其离路灯的距离BD为6米，两棵榕树的影长DE，GH均为4米，两棵树之间的距离DG为6米，求榕树FG的高度；(3)、无论太阳光还是点光源，其本质与视线问题相同．日常生活中我们也可以直接利用视线解决问题．如图②，建筑物CD高为50米，建筑物MF上有一个广告牌EM，合计总高度EF为70米，两座建筑物之间的直线距离FD为30米．一个观测者（身高不计）先站在A处观测，发现能看见广告牌EM的底端M处，观测者沿着直线AF向前走了5米到B处观测，发现刚好看到广告牌EM的顶端E处．则广告牌EM的高度为 米．17. 如图，在安装路灯AB的路面CD比种植树木的地面PQ高 ， 身高的红英MN站在距离C点15米的路面上．在路灯的照射下，路基CP留在地面上的影长EP为0.4米，
(1)、画出红英MN在地面的影子NF；(2)、若红英留在路面上的影长NF为3m，求路灯AB的高度．18.(1)、从A，B两题中任选一题解答，我选择 ．
A、如图（1）是两棵树在同一盏路灯下的影子．①确定该路灯泡所在的位置；②如果此时小颖所在位置恰好与这两棵树所在的位置共线（三点在一条直线上），请画出图中表示小颖影子的线段AB B、如图（2），小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他在某一灯光下的影子为DA，继续按此速度行走2秒到达点F，此时他在同一灯光下的影子落在其身后的线段DF上，测得此时影长MF为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H．他在同一灯光下的影子恰好是HB．图中线段CD，EF，GH表示小明的身高．(2)、请在图中画出小明的影子MF；(3)、若A、B两地相距12米，则小明原来的速度为 ．19.如图，小明与同学合作利用太阳光线测量旗杆的高度，身高1.6m的小明落在地面上的影长为BC=2.4m．
(1)、请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG；(2)、若小明测得此刻旗杆落在地面的影长EG=16m，请求出旗杆DE的高度．20. 如图，是小亮晚上在广场散步的示意图，图中线段 表示站立在广场上的小亮，线段 表示直立在广场上的灯杆，点P表示照明灯的位置．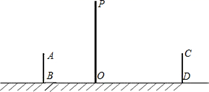
(1)、在小亮由B处沿 所在的方向行走到达O处的过程中，他在地面上的影子长度越来越（用“长”或“短”填空）；请你在图中画出小亮站在 处的影子 ；(2)、当小亮离开灯杆的距离 时，身高为 的小亮的影长为 ，①灯杆的高度为多少m？
②当小亮离开灯杆的距离 时，小亮的影长变为多少m？