【基础版】北师大版数学九年级上册 5.1投影 同步练习
试卷更新日期:2024-10-02 类型:同步测试
一、选择题
-
1. 下列结论中正确的是( )
①在阳光照射下,同一时刻的物体,影子的方向是相同的.②物体在任何光线照射下影子的方向都是相同的.③固定的物体在路灯照射下,影子的方向与路灯的位置有关.④固定的物体在光线照射下,影子的长短仅与物体的长短有关.
A、①③ B、①③④ C、①④ D、②④2. 在一间黑屋子里用一盏白炽灯照如图所示的球,球在地面上的影子是圆形,当把球竖直向上靠近白炽灯时,影子的大小会怎样变化( )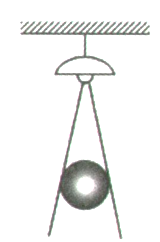 A、越来越小 B、越来越大 C、大小不变 D、不能确定3. 在一个晴朗的上午,乐乐拿着一块长方形木板在地面上形成的投影中不可能是( )A、
A、越来越小 B、越来越大 C、大小不变 D、不能确定3. 在一个晴朗的上午,乐乐拿着一块长方形木板在地面上形成的投影中不可能是( )A、 B、
B、 C、
C、 D、
D、 4. 小明和爸爸晚上散步(小明身高没有爸爸高),在同一个路灯下,小明的影子比爸爸的影子长,这时候爸爸和小明离路灯的距离谁近一点?A、一样近 B、爸爸近一点 C、小明近一点 D、无法比较5. 一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是( )号窗口
4. 小明和爸爸晚上散步(小明身高没有爸爸高),在同一个路灯下,小明的影子比爸爸的影子长,这时候爸爸和小明离路灯的距离谁近一点?A、一样近 B、爸爸近一点 C、小明近一点 D、无法比较5. 一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是( )号窗口 A、1 B、2 C、3 D、46. 小乐用一块长方形硬纸板在阳光下做投影试验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )A、三角形 B、线段 C、矩形 D、正方形7. 如图,在一间屋子里的屋顶上挂着一盏白炽灯,在它的正下方有一个球,下列说法:①球在地面上的影子是圆;②当球向上移动时,它的影子会增大;③当球向下移动时,它的影子会增大;④当球向上或向下移动时,它的影子大小不变,其中正确的有( )
A、1 B、2 C、3 D、46. 小乐用一块长方形硬纸板在阳光下做投影试验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )A、三角形 B、线段 C、矩形 D、正方形7. 如图,在一间屋子里的屋顶上挂着一盏白炽灯,在它的正下方有一个球,下列说法:①球在地面上的影子是圆;②当球向上移动时,它的影子会增大;③当球向下移动时,它的影子会增大;④当球向上或向下移动时,它的影子大小不变,其中正确的有( ) A、0个 B、1个 C、2个 D、3个8. 如图,身高为1.6 m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2 m,AB=10 m,则旗杆的高度是( )
A、0个 B、1个 C、2个 D、3个8. 如图,身高为1.6 m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2 m,AB=10 m,则旗杆的高度是( ) A、6.4m B、7m C、8m D、9m
A、6.4m B、7m C、8m D、9m二、填空题
-
9. 如图,日晷是我国古代利用日影测定时刻的仪器,晷针在晷面上所形成的投影属于投影.
 10. 夜晚小明在路灯下散步,离路灯越近,他的影子越(填“长”或“短”).11. 早在多年前的宋朝,手影就已经作为民间一种有趣的游戏而存在.诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指送诙谐.有时明月灯窗下,一笑还从掌握来”.手影戏全凭手影艺人的十指借光弄影,表演各色人物、花草虫鱼、飞禽走兽甚至是寓言故事.如图,手影戏中的手影属于(填“平行投影”或“中心投影”).
10. 夜晚小明在路灯下散步,离路灯越近,他的影子越(填“长”或“短”).11. 早在多年前的宋朝,手影就已经作为民间一种有趣的游戏而存在.诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指送诙谐.有时明月灯窗下,一笑还从掌握来”.手影戏全凭手影艺人的十指借光弄影,表演各色人物、花草虫鱼、飞禽走兽甚至是寓言故事.如图,手影戏中的手影属于(填“平行投影”或“中心投影”). 12. 数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地面上的影长为2.4米,则树高为米.
12. 数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地面上的影长为2.4米,则树高为米. 13. 如图所示的4个几何体中,正投影可能是四边形的几何体共有个.
13. 如图所示的4个几何体中,正投影可能是四边形的几何体共有个.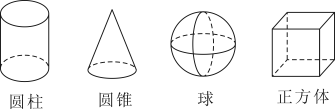
三、解答题
-
14. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关因此,他们认为:可以借助物体的影子长度计算光源到物体的位置于是,他们做了以下尝试.
 (1)、如图 , 垂直于地面放置的正方形框架 , 边长为 , 在其上方点处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为那么灯泡离地面的高度为多少.(2)、不改变图中灯泡的高度,将两个边长为的正方形框架按图摆放,请计算此时横向影子 , 的长度和为多少?15. 已知:如图,和是直立在地面上的两根立柱, , 某一时刻,在阳光下的投影 .
(1)、如图 , 垂直于地面放置的正方形框架 , 边长为 , 在其上方点处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为那么灯泡离地面的高度为多少.(2)、不改变图中灯泡的高度,将两个边长为的正方形框架按图摆放,请计算此时横向影子 , 的长度和为多少?15. 已知:如图,和是直立在地面上的两根立柱, , 某一时刻,在阳光下的投影 . (1)、请你在图中画出此时在阳光下的投影,并简述画图步骤和说明作图依据了太阳光线的哪一性质;(2)、在测量的投影长时,同时测出在阳光下的投影长为 , 请你计算的长.16. 如图,小树AB在路灯O的照射下形成投影BC .
(1)、请你在图中画出此时在阳光下的投影,并简述画图步骤和说明作图依据了太阳光线的哪一性质;(2)、在测量的投影长时,同时测出在阳光下的投影长为 , 请你计算的长.16. 如图,小树AB在路灯O的照射下形成投影BC . (1)、此光源下形成的投影属于 . (填“平行投影”或“中心投影”)(2)、已知树高AB为2m,树影BC为3m,树与路灯的水平距离BP为4.5m.求路灯的高度OP .17. 如图,河对岸有一路灯杆 , 在灯光下,小明在点D处,自己的影长 , 沿方向到达点F处再测自己的影长 , 如果小明的身高为 , 求路灯杆的高度.
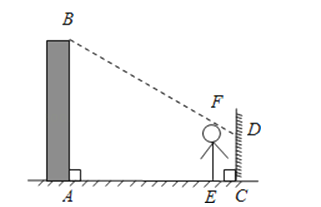
(1)、此光源下形成的投影属于 . (填“平行投影”或“中心投影”)(2)、已知树高AB为2m,树影BC为3m,树与路灯的水平距离BP为4.5m.求路灯的高度OP .17. 如图,河对岸有一路灯杆 , 在灯光下,小明在点D处,自己的影长 , 沿方向到达点F处再测自己的影长 , 如果小明的身高为 , 求路灯杆的高度. 18. 李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
18. 李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.