浙教版(2024)数学七年级上册《第6章 图形的初步知识》单元同步测试卷
试卷更新日期:2024-10-02 类型:单元试卷
一、选择题(每题3分,共30分
-
1. 用一个平面去截下列几何体,截面一定是圆的是( )A、
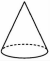 B、
B、 C、
C、 D、
D、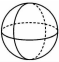 2. 下列四个生活中的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要确定两棵树的位置,就能确定这一行树所在的直线;③从地到地架设电线,总是尽可能沿着线段方向架设;④把弯曲的公路改直,就能缩短路程.其中可以用基本事实“两点确定一条直线”来解释的有( )A、①② B、①③ C、②③ D、③④3. 如图,能用、、三种方法表示同一个角的是A、
2. 下列四个生活中的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要确定两棵树的位置,就能确定这一行树所在的直线;③从地到地架设电线,总是尽可能沿着线段方向架设;④把弯曲的公路改直,就能缩短路程.其中可以用基本事实“两点确定一条直线”来解释的有( )A、①② B、①③ C、②③ D、③④3. 如图,能用、、三种方法表示同一个角的是A、 B、
B、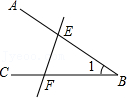 C、
C、 D、
D、 4. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( )
4. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( ) A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线5. 如图,用三角板比较与的大小,其中正确的是( )
A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线5. 如图,用三角板比较与的大小,其中正确的是( ) A、 B、 C、 D、不能确定6. 如图,点D是线段AB的中点,C是线段AD的中点,若AB=16cm,则线段CD=( )cm.
A、 B、 C、 D、不能确定6. 如图,点D是线段AB的中点,C是线段AD的中点,若AB=16cm,则线段CD=( )cm. A、2 B、4 C、8 D、167. 如图所示,已知∠AOC=∠BOD=80°,∠BOC=30°,则∠AOD的度数为( )
A、2 B、4 C、8 D、167. 如图所示,已知∠AOC=∠BOD=80°,∠BOC=30°,则∠AOD的度数为( )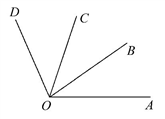 A、160° B、110° C、130° D、140°8. 已知 , , , 则相等的两个角是( )A、 B、 C、 D、无法确定9. 已知线段 , , 且A,B,C三点在同一直线上,则线段AC的长度为( )A、1cm B、1cm或9cm C、2cm或8cm D、9cm10. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中与互余的是( )
A、160° B、110° C、130° D、140°8. 已知 , , , 则相等的两个角是( )A、 B、 C、 D、无法确定9. 已知线段 , , 且A,B,C三点在同一直线上,则线段AC的长度为( )A、1cm B、1cm或9cm C、2cm或8cm D、9cm10. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中与互余的是( ) A、图① B、图② C、图③ D、图④
A、图① B、图② C、图③ D、图④二、填空题(每题3分,共18分)
-
11. 朱自清的《春》中有描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这种现象可以用数学知识解释为 .12. 若把化成以度为单位,则结果为 .13. 如图,一副三角板中,将一个三角板角的顶点与另一个三角板的直角顶点重合,如果 , 那么的大小是 度.
 14. 如图,BC=4cm , BD=7cm , 点D是AC的中点,则AC=cm .
14. 如图,BC=4cm , BD=7cm , 点D是AC的中点,则AC=cm . 15. 如图,已知点C在直线上,平分 , 平分 , 则 .
15. 如图,已知点C在直线上,平分 , 平分 , 则 . 16. 将一副直角三角尺如图放置,若 , 则的度数是.
16. 将一副直角三角尺如图放置,若 , 则的度数是.
三、解答题(共7题,共72分)
-
17. 如图,点O在直线AB上,∠COD=90°,OE平分∠BOC.
 (1)、如图1,若∠DOE=12°,求∠AOC的度数;(2)、如图2,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).18. 如图,点C在线段AB上,点M,N分别是AC,BC的中点.
(1)、如图1,若∠DOE=12°,求∠AOC的度数;(2)、如图2,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).18. 如图,点C在线段AB上,点M,N分别是AC,BC的中点. (1)、若AC=9cm,CB=6cm,求线段MN的长;(2)、若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,求线段MN的长.19. 如图,∠AOB=90°,OP平分∠AOB,OQ平分∠AOC,∠POQ=70°.
(1)、若AC=9cm,CB=6cm,求线段MN的长;(2)、若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,求线段MN的长.19. 如图,∠AOB=90°,OP平分∠AOB,OQ平分∠AOC,∠POQ=70°.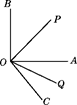 (1)、求∠AOP的度数;(2)、求∠AOC与∠BOC的度数.20. 已知一道路沿途5个车站A、B、C、D、E,它们之间的距离如图所示(km)
(1)、求∠AOP的度数;(2)、求∠AOC与∠BOC的度数.20. 已知一道路沿途5个车站A、B、C、D、E,它们之间的距离如图所示(km) (1)、求D、E两站之间的距离;(2)、如果a=8,D为线段AE的中点,求b的值.21. 已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.(1)、如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
(1)、求D、E两站之间的距离;(2)、如果a=8,D为线段AE的中点,求b的值.21. 已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.(1)、如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置; (2)、求(1)中∠MON的度数,要求写出计算过程;(3)、当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)22. 如图,在同一平面内有四个点A、B、C、D.
(2)、求(1)中∠MON的度数,要求写出计算过程;(3)、当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)22. 如图,在同一平面内有四个点A、B、C、D.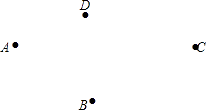 (1)、请按要求作出图形(注:此题作图不需要写出画法和结论)
(1)、请按要求作出图形(注:此题作图不需要写出画法和结论)①作射线AC;
②作直线BD,交射线AC相于点O;
③分别连接AB、AD;
④求作一条线段MN,使其等于AC﹣AB(用尺规作图,保留作图痕迹).
(2)、观察B、D两点间的连线,我们容易判断出线段AB+AD>BD,理由是;(3)、若已知线段AC=80cm,小虫甲从点A出发沿AC向C爬行,速度是2cm/s;小虫乙从点C出发沿线段CA向A爬行,速度是3cm/s,经过t秒钟后,两只小虫相距25cm,请确定t的值.23. 如图,数轴上有A , B两点,A , B之间距离为15,原点O在A , B之间,O到A的距离是O到B的距离的两倍. (1)、点A表示的数为 , 点B表示的数为;(2)、点A、点B和点P(点P初始位置在原点O)同时向左运动,它们的速度分别为1,2,2个单位长度每秒,则经过多少秒,点P到点A与点B的距离相等?(3)、点B沿着数轴移动,每次只允许移动1个单位长度,经过6次移动后,点B与原点O相距1个单位长度.满足条件的点B的移动方法共有多少种?(4)、点A和点B同时沿着数轴移动,两点每次均只允许移动1个单位长度.请判断点A和点B经过相同次数的移动后,能否同时到达原点O?如果能,请给出点A和点B各自的移动方法;如果不能,请说明理由.
(1)、点A表示的数为 , 点B表示的数为;(2)、点A、点B和点P(点P初始位置在原点O)同时向左运动,它们的速度分别为1,2,2个单位长度每秒,则经过多少秒,点P到点A与点B的距离相等?(3)、点B沿着数轴移动,每次只允许移动1个单位长度,经过6次移动后,点B与原点O相距1个单位长度.满足条件的点B的移动方法共有多少种?(4)、点A和点B同时沿着数轴移动,两点每次均只允许移动1个单位长度.请判断点A和点B经过相同次数的移动后,能否同时到达原点O?如果能,请给出点A和点B各自的移动方法;如果不能,请说明理由.