浙教版（2024）数学七年级上册《第4章代数式》单元提升测试卷

试卷更新日期：2024-10-02 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列说法中正确的是（）

A、－a不是单项式 B、 $- \frac{a b c}{2}$ 的系数是－2 C、 $- \frac{x^{2} y^{2}}{3}$ 的系数是 $- \frac{1}{3}$ ，次数是4 D、x²y的系数为0，次数为2

查看试题解析
2. 已知x(x-3)=2，那么多项式-2x²+6x+9的值是( )

A、4 B、5 C、6 D、7

查看试题解析
3. 按下面的运算程序计算：
当输入 $n = 6$ 时，输出结果为33；当输入 $n = 7$ 时，输出结果为17．如果输入n的值为正整数，输出的结果为25，那么满足条件的n的值最多有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列单项式中， $a b^{3}$ 的同类项是( )

A、 $3 a b^{3}$ B、 $2 a^{2} b^{3}$ C、 $- a^{2} b^{2}$ D、 $a^{3} b$

查看试题解析
5. 如图，某长方形花园的长为 $(x + y)$ 米，宽为 $(x - y)$ 米，现根据实际需要对该花园进行整改，长方形花园的长增加 $(x - y)$ 米，宽增加 $(x - 2 y)$ 米，则整改后该花园的周长为（）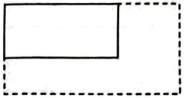

A、 $(4 x - 3 y)$ 米 B、 $(4 x - 6 y)$ 米 C、 $(8 x - 3 y)$ 米 D、 $(8 x - 6 y)$ 米

查看试题解析
6. 若 $A = x^{2} y + 2 x + 3 ， B = - 2 x^{2} y + 4 x$ ，则 $2 A - B =$ （）．

A、3 B、6 C、 $4 x^{2} y + 6$ D、 $4 x^{2} y + 3$

查看试题解析
7. 把六张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为acm ，宽为bcm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（　　）

A、4bcm B、（3a+b）cm C、（2a+2b）cm D、（a+3b）cm

查看试题解析
8. $- (a - b + c)$ 变形后的结果是（　　）

A、 $- a + b + c$ B、 $- a + b - c$ C、 $- a - b + c$ D、 $- a - b - c$

查看试题解析
9. 已知多项式A＝2x³﹣2mx²+3x﹣1，B＝﹣x³+2x²+nx+6，若A﹣B的结果中不含x²和x项，则m ， n的值为（　　）

A、m＝﹣1，n＝3 B、m＝﹣1，n＝﹣3 C、m＝1，n＝3 D、m＝1，n＝﹣3

查看试题解析
10. 若代数式 $x^{2} + a x - (b x^{2} - x - 3)$ 的值与 $x$ 的取值无关，则 $b - a$ 的值为（）

A、 $- 1$ B、1 C、0 D、2

查看试题解析

二、填空题（每题3分，共18分）

11. 当x=1时，代数式 $p x^{3} + q x + 1$ 的值为2026，则当x=-1时，代数式 $p x^{3} + q x + 1$ 的值为

查看试题解析
12. 若单项式2x²y^m与﹣xⁿy³是同类项，则m+n＝．

查看试题解析
13. 当 $k =$ 时，代数式 $x^{2} - 8 + x y - 3 y^{2} + 2 k x y$ 中不含 $x y$ 项．

查看试题解析
14. 如图是 $1$ 个纸杯和若干个叠放在一起的纸杯的示意图，在探究纸杯叠放在一起后的总高度 $H$ 与杯子数量 $n$ 的变化规律的活动中，我们可以获得以下数据 $($ 字母 $)$ ，请选用适当的字母表示 $H =$ ．
$①$ 杯子底部到杯沿底边的高 $h$ ；
$②$ 杯口直径 $D$ ；
$③$ 杯底直径 $d$ ；
$④$ 杯沿高 $a$ ．

查看试题解析
15. 如图1，将一个边长为a的正方形纸片剪去两个小矩形，得到一个“ ”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为．

查看试题解析
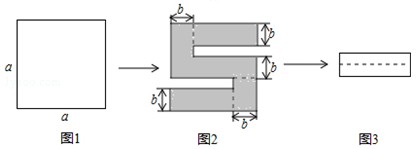16. 把六张形状大小完全相同的小长方形卡片（如图1）不重叠地放在一个底面为长方形（长为 $y cm$ ，宽为 $x cm$ ）的盒子底部（如图2），盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是 $cm$ .（用含 $x$ 或 $y$ 的代数式来表示）

查看试题解析

三、解答题（共10题，共72分）

17. 先化简，再求值： $- a^{2} b + 2 (3 a b^{2} - a^{2} b) - 3 (a b^{2} - a^{2} b)$ ，其中 $a = 1$ ， $b = - 2$ .

查看试题解析
18. 先化简再求值： $3 x - 2 (x^{2} - \frac{1}{2} y^{2}) + (x - \frac{1}{2} y^{2})$ ，其中 $x = 2$ ， $y = - 1$ ．

查看试题解析
19. 先化简，再求值： $2 (x^{2} y + 2 x y^{2}) - (x^{2} y - 1) - 4 x y^{2} - 2$ ，其中 $x = - 2$ ， $y = 2$ ．

查看试题解析
20. 先化简，再求值： $5 x^{2} - 2 (y^{2} + 4 x y) + (2 y^{2} - 5 x^{2})$ ，其中 $| x + \frac{1}{8} | + {(y - 1)}^{2} = 0$ ．

查看试题解析
21. 已知 A=2x²﹣9x﹣11，B=﹣6x+3x²+4，且B+C=A

(1)、求多项式C；

(2)、求 $\frac{1}{2}$ A+2B的值．

查看试题解析
22. 已知 $A = 2 a^{2} - 3 a b$ ， $B = a^{2} + a b$ ．

(1)、化简： $A + 2 B$ ；

(2)、若 $A$ 与 $2 B + C$ 互为相反数，当 $a = - 1$ ， $b = 2$ 时，求 $C$ 的值．

查看试题解析
23. 吕阿姨买了一套新房，她准备将地面全铺上地板砖，这套新房的平面图如图所示（单位： $m$ ），请解答下列问题：

(1)、用含 $a ， b$ 的代数式表示这套新房的面积；

(2)、若 $1 m^{2}$ 地板砖的费用为90元，当 $a = 5 ， b = 6$ 时，这套新房铺地板砖所需的总费用是多少元？

查看试题解析
24. 绿源超市销售茶壶、茶杯，茶壶每只定价50元，茶杯每只定价6元．春节期间，超市将开展促销活动，向顾客提供两种优惠方案：
方案一：每买一只茶壶就赠一只茶杯；
方案二：茶壶和茶杯都按定价的90%付款．
某顾客计划到该超市购买茶壶8只和茶杯x只（茶杯数多于8只）．

(1)、用含x的代数式分别表示方案一与方案二各需付款多少元？

(2)、当 $x = 15$ 时，请通过计算说明该顾客选择上面的两种购买方案哪种更省钱？

查看试题解析
25. 新学期，两摞规格相同的数学课本整齐的叠放在讲台上，请根据图中所给出的数据信息，解答下列问题：

(1)、每本书的高度为cm，课桌的高度为cm；

(2)、当课本数为x（本）时，请写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含x的代数式表示）；

(3)、桌面上有55本与题（1）中相同的数学课本，整齐叠放成一摞，若有18名同学各从中取走1本，求余下的数学课本高出地面的距离．

查看试题解析
26. 【教材呈现】下图是华师版七年级上册数学教材第117页的部分内容．
【阅读理解】
小明通过观察发现：
x²+x+3→2x²+2x﹣3
前后两个多项式中，含x次数相同项的系数存在相同的倍数关系．
思考：只需求得x²+x的值即可求得2x²+2x的值，进而解决问题．
于是他在做作业时采用了如下方法：
由题意，得x²+x+3＝7，则有x²+x＝4．
2x²+2x﹣3＝2（x²+x）﹣3＝2×4﹣3＝5．
所以代数式2x²+2x﹣3的值为5．
【方法学习】
这种方法叫整体代入法，是我们在整式求值时常用到的一种方法，即题目已知条件告诉我们的不是单个未知数的值，而是一个或者几个式子的值，让我们根据条件去求其它代数式的值．这个时候，我们要将问题中的式子转化成含有已知式子的形式，然后整体将已知条件代入求值．

(1)、【方法运用】
若代数式x²+2x+2的值为5，求代数式2x²+4x+3的值．

(2)、当x＝1时，代数式ax³+bx+3的值为9．当x＝﹣1时，求代数式ax³+bx+3的值．

(3)、【方法拓展】
若2a²﹣3ab＝16，2ab﹣b²＝﹣12，则代数式2a²﹣5ab+b²的值为．

查看试题解析

浙教版（2024）数学七年级上册《第4章 代数式》单元提升测试卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共10题，共72分）

浙教版（2024）数学七年级上册《第4章代数式》单元提升测试卷