【培优版】北师大版数学九年级上册第四章 图形的相似 章节测试卷
试卷更新日期:2024-10-01 类型:单元试卷
一、选择题(每题3分,共24分)
-
1. 如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )
 A、1个 B、2个 C、3个 D、4个2. 如图,在等腰中,分别在边上, , , 若已知的长,则能求出下列哪个量( )
A、1个 B、2个 C、3个 D、4个2. 如图,在等腰中,分别在边上, , , 若已知的长,则能求出下列哪个量( ) A、的周长 B、的面积 C、的周长 D、的面积3. 如图,已知AB=AC , ∠B<30°,BC上一点D满足∠BAD=120°,= , 则的值为( )
A、的周长 B、的面积 C、的周长 D、的面积3. 如图,已知AB=AC , ∠B<30°,BC上一点D满足∠BAD=120°,= , 则的值为( ) A、 B、 C、 D、4. 如图,在正方形ABCD中,点E在边CD上,点H在边AD上,CE=DH , CH交BE于点F , 交BD于点G , 连接GE . 下列结论:①CH=BE;②CH⊥BE;③S△GCE=S△GDH;④当E是CD的中点时,;⑤当EC=2DE时,S正方形ABCD=6S四边形DEGH . 其中正确结论的序号是( )
A、 B、 C、 D、4. 如图,在正方形ABCD中,点E在边CD上,点H在边AD上,CE=DH , CH交BE于点F , 交BD于点G , 连接GE . 下列结论:①CH=BE;②CH⊥BE;③S△GCE=S△GDH;④当E是CD的中点时,;⑤当EC=2DE时,S正方形ABCD=6S四边形DEGH . 其中正确结论的序号是( ) A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤5. 如图,正方形中,平分 , 交于点E , 将绕点B顺时针旋转得到 , 延长交于点G , 连接交于点H .
A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤5. 如图,正方形中,平分 , 交于点E , 将绕点B顺时针旋转得到 , 延长交于点G , 连接交于点H .下列结论①;②;③;④
正确的是( )
 A、①②③④ B、②③ C、①③ D、①②④6. 如图,正方形的对角线相交于 , 点 , 分别是边 , 上的动点(不与点 , , 重合), , 分别交于 , 两点,且 , 则下列结论:
A、①②③④ B、②③ C、①③ D、①②④6. 如图,正方形的对角线相交于 , 点 , 分别是边 , 上的动点(不与点 , , 重合), , 分别交于 , 两点,且 , 则下列结论:①;②;③;④是等腰三角形.其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共15分)
-
7. 如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 .
 8. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.将小正方形对角线双向延长,分别交边 , 和边的延长线于点G,H.若大正方形与小正方形的面积之比为5, , 则大正方形的边长为 .
8. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.将小正方形对角线双向延长,分别交边 , 和边的延长线于点G,H.若大正方形与小正方形的面积之比为5, , 则大正方形的边长为 .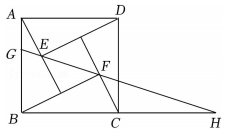 9. 在中, , , 连接 , 若 , , 的面积为7.5,则 .
9. 在中, , , 连接 , 若 , , 的面积为7.5,则 . 10. 如图,在等边三角形中, , 点是边上一点,且 , 点是边上一动点(、两点均不与端点重合),作 , 交边于点 . 若 , 当满足条件的点有且只有一个时,则的值为 .
10. 如图,在等边三角形中, , 点是边上一点,且 , 点是边上一动点(、两点均不与端点重合),作 , 交边于点 . 若 , 当满足条件的点有且只有一个时,则的值为 .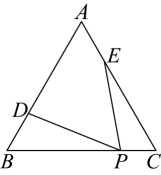
三、解答题(共7题,共61分)
-
11. 如图, , 且 , E是AB的中点,F是边BC上的动点(F不与B , C重合),EF与BD相交于点M .
 (1)、求证:;(2)、若F是BC的中点, , 求BM的长;(3)、若 , BD平分 , 点P是线段BD上的动点,是否存在点P使 , 若存在,求出的度数;若不存在,请说明理由.12. 在中, , , .点在线段上运动,过点作的垂线交线段(如图1)或线段的延长线(如图2)于点 .
(1)、求证:;(2)、若F是BC的中点, , 求BM的长;(3)、若 , BD平分 , 点P是线段BD上的动点,是否存在点P使 , 若存在,求出的度数;若不存在,请说明理由.12. 在中, , , .点在线段上运动,过点作的垂线交线段(如图1)或线段的延长线(如图2)于点 .图1
 图2
图2  备用图
备用图 (1)、当点在线段上时,求证:;(2)、当点与点重合时,求的长;(3)、若点从点以每秒2个单位长的速度向点运动,求点与点的距离不大于1的时长;(4)、当为等腰三角形时,直接写出的长.13. 如图, , 点P为内一点,连接 , 已知 .
(1)、当点在线段上时,求证:;(2)、当点与点重合时,求的长;(3)、若点从点以每秒2个单位长的速度向点运动,求点与点的距离不大于1的时长;(4)、当为等腰三角形时,直接写出的长.13. 如图, , 点P为内一点,连接 , 已知 . (1)、求证:;(2)、若 , 试求的值.14. 如图,点P是菱形的对角线上一点,连接并延长,交于点E , 交的延长线于点F .
(1)、求证:;(2)、若 , 试求的值.14. 如图,点P是菱形的对角线上一点,连接并延长,交于点E , 交的延长线于点F . (1)、求证:;(2)、求证:;(3)、求证: .15. 阅读下面材料:小吴遇到这样一个问题:如图1,在中,是边上的中线,点在边上,与相交于点 , 求的值.
(1)、求证:;(2)、求证:;(3)、求证: .15. 阅读下面材料:小吴遇到这样一个问题:如图1,在中,是边上的中线,点在边上,与相交于点 , 求的值.
小吴发现,过点作 , 交的延长线于点 , 通过构造 , 经过推理和计算能够使问题得到解决(如图2).
(1)、请回答:的值为 .(2)、如图3,在中,点在的延长线上, , 点在上,且 . 求的值;(3)、如图4,在中,点在的延长线上, , 点在上,且 , 直接写出的值为 .16. 请阅读下列材料,并完成相应的任务.梅涅劳斯是公元世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍梅涅劳斯发现,若一条直线与三角形的三边或其延长线相交交点不能是三角形的顶点 , 可以得到六条线段,三条不连续线段的乘积等于剩下三条线段的乘积该定理被称为梅涅劳斯定理,简称梅氏定理.

如图 , 直线交线段于点 , 交线段于点 , 交延长线于点 , 可截得六条线段、、、、、 , 则这六条线段满足 .
下面是该定理的一部分证明过程:
证明:如图 , 过点作 , 交延长线于点 , 则有依据 ,
(1)、上述过程中的依据指的是 ;(2)、请将该定理的证明过程补充完整;(3)、在图中,若点是的中点, , 则的值为 ;(4)、在图中,若 , , 则的值为 .17. 学校数学社团遇到这样一个题目:
如图1,在中,点在线段上,求AB的长.
经过社团成员讨论发现,过点作 , 交AO的延长线于点 , 通过构造就可以解决问题(如图2).
(1)、请回答:°。 .(2)、请参考以上解决思路,解决问题:如图3,在四边形ABCD中,对角线AC与BD相交于点 , , , 求DC的长.