【提升版】北师大版数学九年级上册第四章 图形的相似 章节测试卷
试卷更新日期:2024-10-01 类型:单元试卷
一、选择题(每题3分,共24分)
-
1. 如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
 A、
A、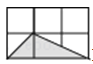 B、
B、 C、
C、 D、
D、 2. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
2. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( ) A、 B、 C、 D、3. 如图,D是△ABC边AB上一点,添加一个条件后,仍然不能使△ACD∽△ABC的是( )
A、 B、 C、 D、3. 如图,D是△ABC边AB上一点,添加一个条件后,仍然不能使△ACD∽△ABC的是( ) A、∠ACB=∠ADC B、∠ACD=∠ABC C、 D、4. 如图,在平行四边形中,E为上一点,且 , 与相交于点F , , 则( ).
A、∠ACB=∠ADC B、∠ACD=∠ABC C、 D、4. 如图,在平行四边形中,E为上一点,且 , 与相交于点F , , 则( ). A、4 B、8 C、12 D、185. 如图,为了估算河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,E,使得A,B与C共线,A,D与E共线,且直线AC与河岸垂直,直线BD,CE均与直线AC垂直.经测量,得到BC,CE,BD的长度,设AB的长为x,则下列等式成立的是 ( )
A、4 B、8 C、12 D、185. 如图,为了估算河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,E,使得A,B与C共线,A,D与E共线,且直线AC与河岸垂直,直线BD,CE均与直线AC垂直.经测量,得到BC,CE,BD的长度,设AB的长为x,则下列等式成立的是 ( ) A、 B、 C、 D、6. 黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形的底边取中点E , 以E为圆心,线段为半径作圆,其与底边的延长线交于点F , 这样就把正方形延伸为矩形 , 称其为黄金矩形.若 , 则( ).
A、 B、 C、 D、6. 黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形的底边取中点E , 以E为圆心,线段为半径作圆,其与底边的延长线交于点F , 这样就把正方形延伸为矩形 , 称其为黄金矩形.若 , 则( ).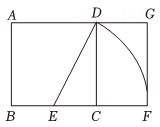 A、 B、 C、 D、7. 如图,在正方形ABCD和CEFG中,连接AF交CD于点H , AB=6,DH=3GH , I是AF的中点,那么CI的长是( )
A、 B、 C、 D、7. 如图,在正方形ABCD和CEFG中,连接AF交CD于点H , AB=6,DH=3GH , I是AF的中点,那么CI的长是( ) A、 B、2 C、 D、38. 如图,在中, , 点D为线段上一动点(不与点B , C重合),连接 , 作 , 交线段于点E .
A、 B、2 C、 D、38. 如图,在中, , 点D为线段上一动点(不与点B , C重合),连接 , 作 , 交线段于点E .下面是某学习小组根据题意得到的结论:
甲同学:;
乙同学:若 , 则;
丙同学:当时,D为的中点.
则下列说法正确的是( )
 A、只有甲同学正确 B、乙和丙同学都正确 C、甲和丙同学正确 D、三个同学都正确
A、只有甲同学正确 B、乙和丙同学都正确 C、甲和丙同学正确 D、三个同学都正确二、填空题(每题3分,共15分)
-
9. 如图,已知▱ABCD中,点E在CD上, ,BE交对角线AC于点F.则 =.
 10. 如图,在正方形网格中,A,B,C,D是网格线交点,AC与BD相交于点O,小正方形的边长为1,则AO的长为 .
10. 如图,在正方形网格中,A,B,C,D是网格线交点,AC与BD相交于点O,小正方形的边长为1,则AO的长为 . 11. 如图,在中,分别是边上的点,将沿翻折至所在的平面内,得相交于点 . 若 , , 则的长是 .
11. 如图,在中,分别是边上的点,将沿翻折至所在的平面内,得相交于点 . 若 , , 则的长是 . 12. 如图,在中, , D , E分别是的中点,把沿着翻折,点B恰好在边上的F处,若 , 则 . (用含k的代数式表示)
12. 如图,在中, , D , E分别是的中点,把沿着翻折,点B恰好在边上的F处,若 , 则 . (用含k的代数式表示) 13. 如图是一边长为6的菱形纸片ABCD,将纸片沿EF折叠,使点D落在边BC上,点A,D的对应点分别为点G,H,GH交AB于点J.若AE=1.4,CF=2,则EJ的长是
13. 如图是一边长为6的菱形纸片ABCD,将纸片沿EF折叠,使点D落在边BC上,点A,D的对应点分别为点G,H,GH交AB于点J.若AE=1.4,CF=2,则EJ的长是
三、解答题(共7题,共61分)
-
14. 如图,在中,D , E分别是上的点,连接 , 且 .
 (1)、求证:;(2)、若 , , , 求的长.15. 如图,在平行四边形ABCD中,过点A作AE⊥BC , 垂足为E , 连接DE , F为线段DE上一点,且∠AFD=∠C .
(1)、求证:;(2)、若 , , , 求的长.15. 如图,在平行四边形ABCD中,过点A作AE⊥BC , 垂足为E , 连接DE , F为线段DE上一点,且∠AFD=∠C . (1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6 , AF=4 , 求AE的长.16. 如图,我们知道,如果点是线段上的一点,将线段分割成两条线段 , 且满足 , 那么这种分割就叫做黄金分割.其中线段与的比值或线段与的比值叫做黄金分割数.已知比例的基本性质:对于长度为的四条线段,如果 , 则 . 求黄金分割数(结果保留根号).
(1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6 , AF=4 , 求AE的长.16. 如图,我们知道,如果点是线段上的一点,将线段分割成两条线段 , 且满足 , 那么这种分割就叫做黄金分割.其中线段与的比值或线段与的比值叫做黄金分割数.已知比例的基本性质:对于长度为的四条线段,如果 , 则 . 求黄金分割数(结果保留根号). 17.(1)、【教材呈现】下图是华师版九年级上册数学教材第77页的部分内容.请根据教材提示,结合图1,写出完整的证明过程.
17.(1)、【教材呈现】下图是华师版九年级上册数学教材第77页的部分内容.请根据教材提示,结合图1,写出完整的证明过程.猜想:
如图1.在中,点、分别是与的中点,根据画出的图形,可以猜想:
, 且 .
对此,我们可以用演绎推理给证明.
 (2)、【结论应用】如图2,是等边三角形,点在边上(点与点、不重合),过点作交于点 , 连结 , 、、分别为、、的中点,顺次连结、、 .
(2)、【结论应用】如图2,是等边三角形,点在边上(点与点、不重合),过点作交于点 , 连结 , 、、分别为、、的中点,顺次连结、、 .
①求证:;
②的大小是 .
18. 如图,在中,是边上一点.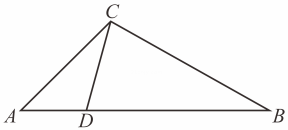 (1)、当时,
(1)、当时,①求证:;
②若 , , 求的长;
(2)、已知 , 若 , 求的长.

