【基础版】北师大版数学九年级上册第四章图形的相似章节测试卷

试卷更新日期：2024-10-01 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共24分）

1. 已知 $\frac{x}{y} = \frac{2}{3}$ ，则下列等式中正确的是（）

A、 $2 x = 3 y$ B、 $\frac{x + y}{y} = \frac{5}{2}$ C、 $\frac{y}{x} = \frac{3}{2}$ D、 $x = 2$ ， $y = 3$

查看试题解析
2. 如图， $l_{1} / / l_{2} / / l_{3}$ ，直线 $A C$ 、 $D F$ 与这三条平行线分别交于点A、B、C和点D、E、F ， $A B = 3$ ， $B C = 6$ ， $D E = 4$ ，则 $D F$ 的长是（）

A、8 B、9 C、11 D、12

查看试题解析
3. 如图， $△ A B C$ 与 $△ D E F$ 位似，点O是它们的位似中心，且它们的周长比为 $2 ︰ 3$ ，则 $△ A O B$ 与 $△ D O E$ 的面积之比是（）

A、 $2 ︰ 3$ B、 $1 ︰ 2$ C、 $4 ︰ 9$ D、 $9 ︰ 4$

查看试题解析
4. 若四条线段 $a$ ， $b$ ， $c$ ， $d$ 成比例，其中 $b = 2 c m$ ， $c = 3 c m$ ， $d = 6 c m$ ，则线段 $a$ 的长为（）

A、 $1 c m$ B、 $2 c m$ C、 $3 c m$ D、 $12 c m$

查看试题解析
5. 如图，把△AOB缩小后得到△COD ，则△COD与△AOB的相似比为（　　）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{3}{2}$ D、 $\frac{5}{2}$

查看试题解析
6. 已知点P是线段AB的黄金分割点（AP＞PB），AB=4，那么AP的长是（）

A、 $2 \sqrt{5} - 2$ B、 $2 - \sqrt{5}$ C、 $2 \sqrt{5} - 1$ D、 $\sqrt{5} - 2$

查看试题解析
7. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ ， $F$ 分别在边 $A B$ ， $A C$ ， $B C$ 上，且 $D E ∥ B C$ ， $E F ∥ A B$ ．若 $A D = 2 B D$ ，则 $\frac{C F}{B F}$ 的值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
8. 如图，AB∥CD，AB=2，CD=3，AD=4，则OD的长为（）

A、 $\frac{8}{3}$ B、 $\frac{8}{5}$ C、 $\frac{12}{7}$ D、 $\frac{12}{5}$

查看试题解析

二、填空题（每题3分，共15分）

9. 如图， $A D ∥ B E ∥ C F$ ，直线l₁、l₂与这三条平行线分别交于点A、B、C和点D、E、F．若 $\frac{A B}{B C} = \frac{2}{3}$ ， $D E = 6$ ，则DF的长为．

查看试题解析
10. 如图，在△ABC中，点D，E分别在AB，AC上，∠AED＝∠B， $A D = \frac{3}{4} A C$ ，若四边形BCED的面积为7，则△ADE的面积为.

查看试题解析
11. 如图，在某校的2023年新年晚会中，舞台AB的长为20米，主持人站在点C处自然得体，已知点C是线段AB上靠近点B的黄金分割点，则此时主持人与点A的距离为米．

查看试题解析
12. 如图， $△ A B C$ 的高AD，BE相交于点O，写出一个与 $△ A O E$ 相似的三角形，这个三角形可以是．

查看试题解析
13. 若原图形上点的坐标为 $(x ， y)$ ，以原点为位似中心，位似图形与原图形的位似比为 $k$ ，则位似图形上的对应点的坐标为或.

查看试题解析

三、解答题（共7题，共61分）

14. 如图，在矩形ABCD中，点E是BC的中点，连接AE ，过点D作AE的垂线分别交AE ， AB于点F ， G ．

(1)、求证： $△ A D F ∽ △ E A B$ ；

(2)、若 $A D = 6$ ， $A F = 2 \sqrt{3}$ ，求AE的长．

查看试题解析
15. 已知 $a = \frac{b}{2} = \frac{c}{3} \neq 0$ 求： $\frac{2 a - b + c}{a + b}$ 的值．

查看试题解析
16. 如图，△ABC∽△ACD ．

(1)、若CD平分∠ACB ， ∠ACD=40° ，求∠ADC的度数.

(2)、若AD＝2，BD＝3，求AC的长．

查看试题解析
17. 如图，已知直线 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 分别截直线 $l_{4}$ 于点 $A$ ， $B$ ， $C$ ，截直线 $l_{5}$ 于点 $D$ ， $E$ ， $F$ ，且 $l_{1} ∥ l_{2} ∥ l_{3}$ .

(1)、如果 $A B = 4$ ， $B C = 8$ ， $E F = 12$ ，求 $D E$ 的长；

(2)、如果 $D E ： E F = 2 ： 3$ ， $A C = 25$ ，求 $A B$ 的长.

查看试题解析
18. 如图，BE是△ABC的角平分线，延长BE至D，使得BC=CD．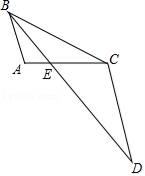

(1)、求证：△AEB∽△CED；

(2)、若AB=2，BC=4，AE=1，求CE长．

查看试题解析
19. 方格图中的每个小方格都是边长为1小正方形，我们把小正方形的顶点称为格点，格点连线为边的四边形称为“格点四边形”，图1中的四边形ABCD就是一个格点四边形.

(1)、小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答：四边形ABCD与四边形EFGH相似吗？若相似，直接写出四边形ABCD与四边形EFGH的相似比；若不相似说明理由；

(2)、请在图3的方格图中画一个格点四边形，使它与四边形ABCD相似，但与四边形ABCD、四边形EFGH都不全等.

查看试题解析
20. 已知：如图， $△ A B C$ 中， $A B = 2$ ， $B C = 4$ ， $D$ 为 $B C$ 边上一点， $B D = 1$ ．

(1)、求证： $△ A B D ∽ △ C B A$ ．

(2)、若 $D E ∥ A B$ 交 $A C$ 于点 $E$ ，请再写出另一个与 $△ A B D$ 相似的三角形，并直接写出 $D E$ 长．

查看试题解析

【基础版】北师大版数学九年级上册第四章 图形的相似 章节测试卷

一、选择题（每题3分，共24分）

二、填空题（每题3分，共15分）

三、解答题（共7题，共61分）

【基础版】北师大版数学九年级上册第四章图形的相似章节测试卷