【培优版】北师大版数学九年级上册4.8图形的位似 同步练习
试卷更新日期:2024-10-01 类型:同步测试
一、选择题
-
1. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )
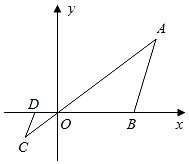 A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)2. 一个面积为的四边形 , 它的位似图形为四边形 , 位似中心为 , 若 , 则四边形的面积为( )A、 B、 C、或 D、以上都不对3. 在平面直角坐标系中,各顶点的坐标分别为: , 以O为位似中心,与位似,若B点的对应点的坐标为 , 则A点的对应点坐标为( )A、 B、 C、 D、4. 在如图所示的肉眼成像的示意图中,可能没有蕴含下列哪项初中数学知识( )
A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)2. 一个面积为的四边形 , 它的位似图形为四边形 , 位似中心为 , 若 , 则四边形的面积为( )A、 B、 C、或 D、以上都不对3. 在平面直角坐标系中,各顶点的坐标分别为: , 以O为位似中心,与位似,若B点的对应点的坐标为 , 则A点的对应点坐标为( )A、 B、 C、 D、4. 在如图所示的肉眼成像的示意图中,可能没有蕴含下列哪项初中数学知识( ) A、平行线的性质 B、相似三角形的判定 C、位似图形 D、旋转5. 如图,在平面直角坐标系中,△OAB的顶点O在坐标原点,顶点A,B的坐标分别为(-2,-1),(-1.5,0).△OCD与△OAB位似,位似中心是原点O,若点D的坐标为(4.5,0),则点C的坐标为( )
A、平行线的性质 B、相似三角形的判定 C、位似图形 D、旋转5. 如图,在平面直角坐标系中,△OAB的顶点O在坐标原点,顶点A,B的坐标分别为(-2,-1),(-1.5,0).△OCD与△OAB位似,位似中心是原点O,若点D的坐标为(4.5,0),则点C的坐标为( )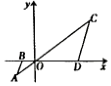 A、(6,3) B、(-6,-3) C、(4,2) D、(-4,-2)6. 下列三个关于位似图形的表述:
A、(6,3) B、(-6,-3) C、(4,2) D、(-4,-2)6. 下列三个关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
其中正确命题的序号是( )
A、①② B、②③ C、①③ D、①②③7. 已知△ABC中,∠BAC=90°,用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形,其作法错误的是( )A、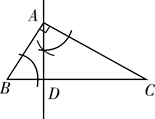 B、
B、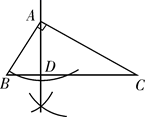 C、
C、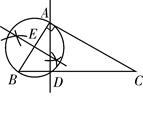 D、
D、 8. 如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(-4,4),(2,1),则位似中心的坐标为( )
8. 如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(-4,4),(2,1),则位似中心的坐标为( ) A、(0,3) B、(0,2.5) C、(0,2) D、(0,1.5)
A、(0,3) B、(0,2.5) C、(0,2) D、(0,1.5)二、填空题
-
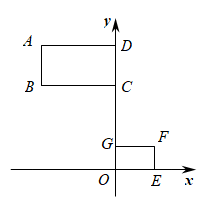
9. 小芳的房间有一面积为的玻璃窗,她站在室内离窗子的地方向外看,她能看到窗前面一幢楼房的面积有.(楼之间的距离为)10. 如图,在直角坐标系中,矩形与矩形位似,矩形的边在y轴上,点B的坐标为 , 矩形的两边都在坐标轴上,且点F的坐标为 , 则矩形与的位似中心的坐标是 .
 11. 如图, 是 内任意一点, 分别为 上的点,且 与 是位似三角形,位似中心为 .若 则 与 的位似比为.
11. 如图, 是 内任意一点, 分别为 上的点,且 与 是位似三角形,位似中心为 .若 则 与 的位似比为.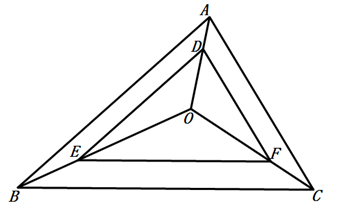 12. 如图,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点为位似中心的位似图形,且相似比为 , 点A1 , A2 , A3在x轴上,延长A3C2交射线OB1于点B3 , 以A3B3为边作正方形A3B3C3A4;延长A4C3交射线OB1于点B4 , 以A4B4为边作正方形A4B4C4A5…,若OA1=2,则正方形A2022B2022C2022A2023的面积是 .
12. 如图,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点为位似中心的位似图形,且相似比为 , 点A1 , A2 , A3在x轴上,延长A3C2交射线OB1于点B3 , 以A3B3为边作正方形A3B3C3A4;延长A4C3交射线OB1于点B4 , 以A4B4为边作正方形A4B4C4A5…,若OA1=2,则正方形A2022B2022C2022A2023的面积是 . 13. 如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为 , 点A、B、D在x轴上,若等边△BDE的边长为6,则点C的坐标为 .
13. 如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为 , 点A、B、D在x轴上,若等边△BDE的边长为6,则点C的坐标为 .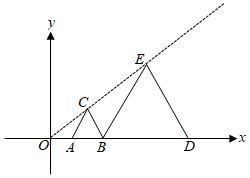
三、解答题
-
14. 放缩尺是一种绘图工具,它能把图形放大或缩小.
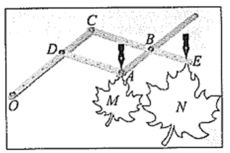
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点, , , 在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接 , , 可证得以下结论:
①和为等腰三角形,则 , (180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③ , 于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.
15. 放缩尺是一种绘图工具,它能把图形放大或缩小.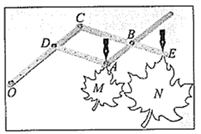
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点 , , , 处连接起来,使得直尺可以绕着这些点转动, 为固定点, , ,在点 , 处分别装上画笔.
画图:现有一图形 ,画图时固定点 ,控制点 处的笔尖沿图形 的轮廓线移动,此时点 处的画笔便画出了将图形 放大后的图形 .
原理:
连接 , ,可证得以下结论:
① 和 为等腰三角形,则 , (180°-∠ ▲ );
②四边形 为平行四边形(理由是 ▲ );
③ ,于是可得 , , 三点在一条直线上;
④当 时,图形 是以点 为位似中心,把图形 放大为原来的 ▲ 倍得到的.
16. 如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)
 17. 视力表对我们来说并不陌生,它蕴含着一定的数学知识.下面我们以标准对数视力表为例,来探索视力表中的奥秘.
17. 视力表对我们来说并不陌生,它蕴含着一定的数学知识.下面我们以标准对数视力表为例,来探索视力表中的奥秘.

用硬纸板复制视力表中所对应的“E”,并依次编号为①,②,放在水平桌面上.如图所示,将②号“E”沿水平桌面向右移动,直至从观测点O看去,对应顶点 , , O在一条直线上为止.这时我们说,在处用①号“E”测得的视力与在处用②号“E”测得的视力相同.
(1)、探究图中与之间的关系,请说明理由;(2)、若 , ①号“E”的测量距离 , 要使测得的视力相同,求②号“E”的测量距离 .18. 数学课上,老师要求同学们在扇形纸片OAB上画出一个正方形,使得正方形的四个顶点分别落在扇形半径OA、OB和弧AB上.有一部分同学是这样画的:如图1,先在扇形OAB内画出正方形CDEF,使得C、D在OA上,F在OB上,连结OE并延长交弧AB与G点,过点G,作GJ⊥OA于点J,作GH⊥GJ交OB于点H,再作HI⊥OA于点I.
(1)请问他们画出的四边形GHIJ是正方形吗?如果是,请给出你的证明;如果不是,请说明理由;
(2)还有一部分同学用另外一种不同于图1的方法画出的,请你参照图1的画法,在图2上画出这个正方形(保留画图痕迹,不要求证明).
19. 如图①,在四边形ABCD的边AB上任取一点P(点P不与A,B重合),分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点”.
解决问题
(1)、如图①,∠A=∠B=∠DPC=50°,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.(2)、如图②,在四边形ABCD中,A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;(3)、如图③,在四边形ABCD中,∠B=∠C=90°,AB=3,CD=5,AD=8.点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.20. 阅读下面材料:小明观察一个由1×1正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1.他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出交点与垂足之间的数值.

请回答:
(1)、如图1,A、B、C是点阵中的三个点,请在点阵中找到点D , 作出线段CD , 使得CD⊥AB;(2)、如图2,线段AB与CD交于点O , 小明在点阵中找到了点E , 连接AE . 恰好满足AE⊥CD于E , 再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.请你帮小明计算:OC=OF=;
(3)、参考小明思考问题的方法,解决问题:如图3,线段AB与CD交于点O . 在点阵中找到点E , 连接AE , 满足AE⊥CD于F . 计算: OC= , OF= .