【提升版】北师大版数学九年级上册4.8图形的位似同步练习

试卷更新日期：2024-10-01 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在平面直角坐标系xOy中，以原点O为位似中心，把线段AB放大后得到线段CD．若点A（1，2），B（2，0），D（5，0），则点A的对应点C的坐标是（）

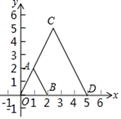A、(2，5) B、( $\frac{5}{2}$ ，5) C、(3，5) D、(3，6)

查看试题解析
2. 如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（）

A、（3，2） B、（3，1） C、（2，2） D、（4，2）

查看试题解析
3. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，位似中心为O ， $O A ： O D = 3 ： 7$ ， $S_{△ A B C} = 9$ ，则 $△ D E F$ 的面积为（）

A、12 B、16 C、21 D、49

查看试题解析
4. 如图， $△ A B C$ 和 $△ D E F$ 是以点O为位似中心的位似图形， $O A ： O D = 2 ： 5$ ， $△ A B C$ 的周长为8，则 $△ D E F$ 的周长为（）

A、12 B、18 C、20 D、24

查看试题解析
5. 如图， $△ A B C$ 与 $△ D E C$ 都是等边三角形，固定 $△ A B C$ ，将 $△ D E C$ 从图示位置绕点C逆时针旋转一周，在 $△ D E C$ 旋转的过程中， $△ D E C$ 与 $△ A B C$ 位似的位置有（）

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个及 $3$ 个以上

查看试题解析
6. 如图， $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 位似，点O为位似中心，若 $△ A B C$ 的周长等于 $△ A^{'} B^{'} C^{'}$ 周长的 $\frac{1}{4}$ ． $A O = 2$ ，则 $O A^{^{'}}$ 的长度为（）

A、4 B、6 C、8 D、10

查看试题解析
7. 如图， $R t △ A B C$ 与 $R t △ E F G$ 是关于 $y$ 轴上一点的位似图形，若 $B (- 4 ， 4)$ ， $F (2 ， 1)$ 则位似中心的坐标为（）

A、 $(0 ， 1)$ B、 $(0 ， 2)$ C、 $(0 ， 3)$ D、 $(0 ， \frac{3}{2})$

查看试题解析
8. 如图，已知 $▱$ ABCD，以B为位似中心作 $▱$ ABCD的位似图形EBFG，位似图形与原图形的位似比为2：3，连结CG、DG．若 $▱$ ABCD的面积为30，则△CDG的面积为（）．

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

9. 如图，点 $O$ 是等边三角形 $P Q R$ 的中心， $P'$ ， $Q'$ ， $R'$ 分别是 $O P$ ， $O Q$ ， $O R$ 的中点，则 $△ P' Q' R'$ 与 $△ P Q R$ 是位似三角形 $.$ 此时， $△ P' Q' R'$ 与 $△ P Q R$ 的位似比为．

查看试题解析
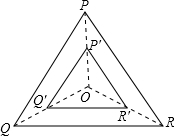10. 如图，在平面直角坐标中， $△ A B C$ 与 $△ D E F$ 是位似图形，且它们的顶点都在格点上，则位似中心的坐标为．

查看试题解析
11. 在平面直角坐标系xOy中，已知点A（﹣1，3），B（﹣6，3），以原点O为位似中心，在同一象限内把线段AB缩短为原来的 $\frac{1}{3}$ ，得到线段CD，其中点C对应点A，点D对应点B，则点D的坐标为．

查看试题解析
12. 在平面直角坐标系中，已知点 $E (- 4 ， 2)$ ， $F (- 1 ， - 1)$ ．以原点O为位似中心，把 $△ E F O$ 放大，使得放大前后对应线段的比为 $1 ： 2$ ，则点E的对应点 $E^{'}$ 的坐标为．

查看试题解析
13. 如图，电影胶片上每一幅图片的规格为3.5cm×3.5cm，放映银幕的规格为3m×3m．若放映机的光源S距胶片1.4cm，则光源S距银幕m时，放映的图像刚好布满整个银幕．

查看试题解析

三、解答题

14. 网格中每个小正方形的边长都是1．

(1)、在图1中画一个格点 $△ A_{1} B_{1} C_{1}$ ，使 $△ A_{1} B_{1} C_{1} ∽ △ A B C$ ，且相似比为2：1；

(2)、在图2中画一个格点 $△ A_{2} B_{2} C_{2}$ ，使 $△ A_{2} B_{2} C_{2} ∽ △ A B C$ ，且相似比为 $\sqrt{2} : 1$ ．

查看试题解析
15. 如图①②都是4×4的正方形网格，每个小正方形的顶点称为格点，已知△ABC的顶点均在格点上．

(1)、在图①中，以格点为顶点，画出一个△DCE与△ACB成位似图形，且位似比为1：2

(2)、在图②中找出AB的一个三等分点点P．辅助线用虚线．

查看试题解析
16. 如图是几组三角形的组合图形，图①中， $△ AOB ∽ △ DOC$ ；图②中， $△ ABC ∽ △ ADE$ ；图③中， $△ ABC ∽ △ ACD$ ；图④中， $△ ACD ∽ △ CBD$ ．
小 $Q$ 说：图①、②是位似变换，其位似中心分别是 $O$ 和 $A$ ．
小 $R$ 说：图③、④是位似变换，其位似中心是点 $D$ ．
请你观察一番，评判小 $Q$ ，小 $R$ 谁对谁错．

查看试题解析
17.
如图，正方形A₁A₂B₁C₁ ， A₂A₃B₂C₂ ， …A_na_n+1B_nC_n ，如图位置依次摆放，已知点C₁ ， C₂ ， C₃…，C_n在直线y=x上，点A₁的坐标为（1，0）．
（1）写出正方形A₁A₂B₁C₁ ， A₂A₃B₂C₂ ， …A_na_n+1B_nC_n ，的位似中心坐标；
（2）正方形A₄A₃B₄C₄四个顶点的坐标．

查看试题解析
18.
如图是一个由8×8个小正方形组成的方格纸，我们把顶点在正方形顶点的三角形称为格点三角形，图中的△ABC就是一个格点三角形，点M是AC的中点．
（1）请在图中作出一个格点△AMN，使△AMN与△ABC相似，并将△AMN绕点A顺时针旋转90°，得到△AEF，使点E与点M对应，请在图中作出△AEF；
（2）请以AF为边作出格点△AFD，使△AFD与△ABC全等．

查看试题解析
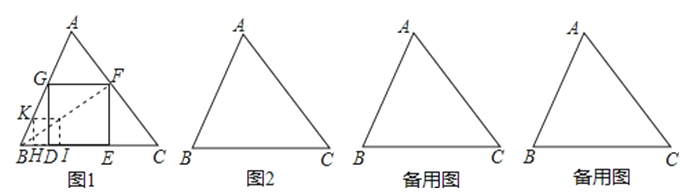
19.
如图1，给定锐角三角形ABC，小明希望画正方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上，他发现直接画图比较困难，于是他先画了一个正方形HIJK，是的H，I，位于射线BC上，K位于射线BA上，而不需要求J必须位于AC上．这是他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG．
阅读以上材料，回答小明接下来研究的以下问题：
（1）如图2，给定锐角三角形ABC，画出所有长宽比为2：1的长方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．
（2）已知三角形ABC的面积为36，BC=12，在第（1）问的条件下，求长方形DEFG的面积．

查看试题解析
20. 阅读下列材料：小华遇到这样一个问题：
已知：如图1，在△ABC中，三边的长分别为AB= $\sqrt{10}$ ，AC= $\sqrt{2}$ ，BC=2，求∠A的正切值．
小华是这样解决问题的：
如图2所示，先在一个正方形网格（每个小正方形的边长均为1）中画出格点△ABC（△ABC三个顶点都在小正方形的顶点处），然后在这个正方形网格中再画一个和△ABC相似的格点△DEF，从而使问题得解．

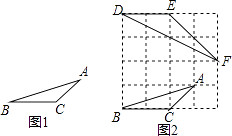(1)、如图2，△DEF中与∠A相等的角为， ∠A的正切值为．

(2)、参考小华的方法请解决问题：若△LMN的三边分别为LM=2，MN=2 $\sqrt{2}$ ，LN=2 $\sqrt{5}$ ，求∠N的正切值．

查看试题解析

【提升版】北师大版数学九年级上册4.8图形的位似 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学九年级上册4.8图形的位似同步练习