【提升版】北师大版数学九年级上册4.6利用相似三角形测高 同步练习
试卷更新日期：2024-09-30 类型：同步测试
一、选择题
-
1. 小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（ ）
A、10米 B、12米 C、15米 D、22.5米2. 图1是伸缩折叠不锈钢晾衣架的实物图，图2是它的侧面示意图，AD和CB相交于点O ， A ， B之间的距离为1.2米，AB∥CD ， 根据图2中的数据可得点C ， D之间的距离为（ ）
A、0.8米 B、0.86米 C、0.96米 D、1米3. 如图，小明在A时测得某树的影长为 ， B时又测得该树的影长为 ， 若两次日照的光线互相垂直，则树的高度为（ ）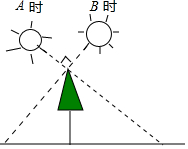
A、 B、 C、 D、4. 《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆AB ， 从木杆的顶端B观察井水水岸D ， 视线BD与井口的直径AC交于点E ， 如果测得米，米，米，那么CD为（ ）米．
A、5 B、4 C、3 D、25. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中第九卷，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”译文：“今有一座长方形小城，东西向城墙长7里，南北向城墙长9里，各城墙正中均开一城门．走出东门15里处有棵大树，问走出南门多少步恰好能望见这棵树？”（注：1里步）你的计算结果是：出南门（ ）步而见木．
A、205 B、215 C、305 D、3156. 如图，已知是一块锐角三角形材料，边 ， 高 ， 要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB ， AC上，这个正方形零件的边长是（ ）
A、48mm B、80mm C、20mm D、46mm7. 如图，图1是装了液体的高脚杯，加入一些液体后如图2所示，则此时液面AB为（ ）
A、5.6cm B、6.4cm C、8cm D、10cm8. 据《九章算术》记载：“今有山居木西，不知其高.山去五十三里，木高九丈五尺.人立木东三里，望木末适与山峰斜平.人目高七尺.问山高几何？”译文如下：如图，今有山 位于树的西面.山高 为未知数，山与树相距53里，树高9丈5尺.人站在离树3里的地方，观察到树梢C恰好与山峰A处在同一条直线上，人眼离地7尺.则山高 的长为（结果保留到整数，1丈=10尺）（ ）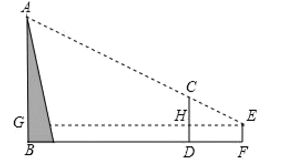
A、162丈 B、163丈 C、164丈 D、165丈二、填空题
-
9. 如图所示，某种品牌小轿车左右两个参照点A和F的距离为米，这两个参照点到地面的距离米，若驾驶员的眼睛点P到地面的距离米，则驾驶员的视野盲区的长度为米．
10. 如图，小峰同学用自制的直角三角形纸板测量树的高度 ， 他调整自己的位置，设法使斜边保持水平，并且与点在同一直线上．已知纸板的两条直角边 ， ， 测得 ， ， 则树高为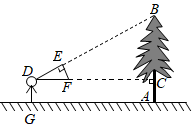
11. 学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO＝6m，AB＝1.2m，CO＝1m，则栏杆C端应下降的垂直距离CD为m.
12. 《九章算术》是我国数学经典，上面记载：“今有邑方不知大小，各中开门．出北门三十步有木，出西门七百五十步见木．问邑方几何？”其意思是：如图，已知正方形小城ABCD ， 点E ， G分别为CD ， AD的中点，EF⊥CD ， GH⊥AD ， 点F ， D ， H在一条直线上，EF＝30步，GH＝750步．问正方形小城ABCD的边长是多少？该问题的答案是 ．
13. 如图1是液体沙漏的立体图形，图2，图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图，则图3中AB＝cm．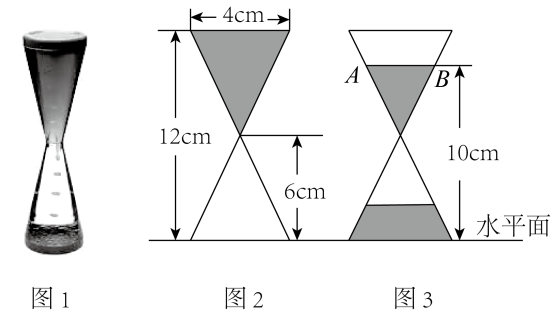
三、解答题
-
14. 小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：
如示意图，小明边移动边观察，发现站到点处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度 m， m， m（点 在同一直线上）．
已知小明的身高是1.7m，请你帮小明求出楼高 （结果精确到0.1m）．
15. 如图1，滹沱河是山西地区一条途经了舟山和太行山的知名河流，这条河流的流域面积达到了2.73万平方公里，其发源地处于山西省繁峙县泰戏山桥儿沟村，这条河流早在《山海经》中就有出现过，被叫做为虔池．为了估算河流的宽度，我们在河的对岸选定一个目标P ， 在近岸取点A和C ， 使点P、A、C共线且与河垂直，接着在过点C且与直线PC垂直的直线上选择适当的点D ， 确定PD与过点A且与PC垂直的直线交点B ， 测得AC＝50m ， CD＝120m ， AB＝80m ， 请根据这些数据求河的宽度PA ．
16. 鹳雀楼（如图1）位于山西省永济市蒲州古城西面的黄河东岸，始建于北周时期，是现存最大的仿唐建筑．某校数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的原理，来测量鹳雀楼的高度．如图2，该小组成员选取与底端B在同一水平地面上的E ， G两点，分别垂直地面竖立两根高为的标杆和 ， 两标杆间隔约为 ． 从标杆后退到点D处（即），从点D处观察顶端A处，使A ， F ， D三点共线；从标杆后退到点C处（即），从点C处观察顶端A处，使A ， H ， C三点共线，其中点A ， B ， C ， D ， E ， F ， G ， H均在同一平面内．请根据上述测量数据，求鹳雀楼的高度．
17. 学习了相似三角形相关知识后，小明和同学们想利用“标杆”测量大楼的高度．如图，小明站立在地面点F处，他的同学在点B处竖立“标杆” ， 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上（点F、B、D也在一条直线上）．已知小明的身高米，“标杆”米，又米，米．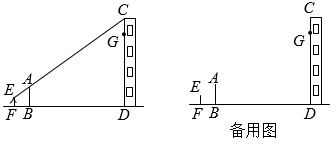
(1)、求大楼的高度为多少米（垂直地面）？(2)、小明站在原来的位置，同学们通过移动标杆，可以用同样的方法测得楼上点G的高度米，那么相对于第一次测量，标杆应该向大楼方向移动米.18. 如图1，在光的反射现象中，反射光线、入射光线和法线都在同一个平面内，反射光线和入射光线分别位于法线两侧，反射角等于入射角 ． 这就是光的反射定律．【问题解决】如图2，林舒同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙，木板和平面镜，手电筒在点处，手电筒的光从平面镜上点处反射后，恰好经过木板的边缘点 ， 落在墙上的点处，点到地面的高度 ， 点到地面的高度 ， 手电筒到木板的水平距离 ， 木板到墙的水平距离为 ． 图中 ， ， ， 在同一条直线上．
(1)、求的长；(2)、求点E到地面的高度的长．19. 学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．
(1)、小丽先调整自己的位置至点P，将直角三角形纸板的三个顶点位置记为A、B、C（如图①），斜边AB平行于地面MN（点M、P、E、N在一直线上），且点D在边AC（较长直角边）的延长线上，此时测得边AB距离地面的高度EF为1.5米，小丽与古树的距离AF为16米，求古树的高度DE；(2)、为了尝试不同的思路，小丽又向前移动自己的位置至点Q，将直角三角形纸板的三个顶点的新位置记为A′、B′、C′（如图②），使直角边B′C′（较短直角边）平行于地面MN（点M、Q、E、N在一直线上），点D在斜边B′A′的延长线上，且测得此时边B′C′距离地面的高度依然是1.5米，那么小丽向前移动了多少米？20. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳，如图是小然站在地面MN欣赏悬挂在墙壁PM上的油画AD（PM⊥MN）的示意图，设油画AD与墙壁的夹角∠PAD＝α，此时小然的眼睛与油画底部A处于同一水平线上，视线恰好落在油画的中心位置E处，且与AD垂直．已知油画的长度AD为100cm．
(1)、视线∠ABD的度数为 .（用含α的式子表示）(2)、当小然到墙壁PM的距离AB＝250cm时，求油画顶部点D到墙壁PM的距离．