【基础版】北师大版数学九年级上册4.6利用相似三角形测高 同步练习
试卷更新日期：2024-09-30 类型：同步测试
一、选择题
-
1. 如图，它是物理学中小孔成像的原理示意图，已知物体 ， 根据图中尺寸 ， 则的长应是（ ）
A、15 B、30 C、20 D、102. 如图，小明同学利用相似三角形测量旗杆的高度，若测得木杆AB长2m，它的影长BC为1m，旗杆DE的影长EF为6m，则旗杆DE的高度为（ ）
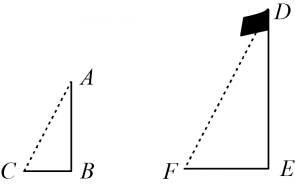A、9m B、10m C、11m D、12m3. 如图，一同学在湖边看到一棵树，他目测出自己与树的距离为20m，树的顶端在水中的倒影距自己5m远，该同学的身高为1.7m，则树高为（ ）m.
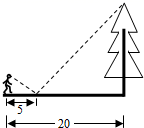A、3.4 B、5.1 C、6.8 D、8.54. 如图所示，树AB在路灯的照射下形成投影AC，已知路灯高 ， 树影 ， 树AB与路灯的水平距离 ， 则树的高度AB是（ ）.
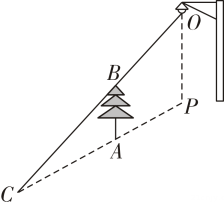A、2m B、3m C、 D、5. 如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上。若测得BE=20m，EC=10m，CD=20m，则河的宽度AB等于（ ）
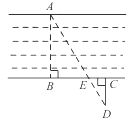A、60m B、40m C、30m D、20m6. 如图．利用标杆BE测量建筑物的高度．已知标杆BE高1.2m ， 测得AB＝1.6m ． BC＝12.4m ． 则建筑物CD的高是（ ）
A、9.3m B、10.5m C、12.4m D、14m7. 如图，铁道口的栏杆短臂OA长1m，长臂OB长8m．当短臂外端A下降0.5m时，长臂外端B升高（ ）
A、2m B、4m C、4.5m D、8m8.如图，路边有一根电线杆AB和一块正方形广告牌（不用考虑牌子的厚度）．有一天，小明突然发现，在太阳光照射下，电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处，而正方形广告牌的影子刚好落在地面上E点，已知BC=5米，正方形边长为2米，DE=4米．则此时电线杆的高度是（ ）米．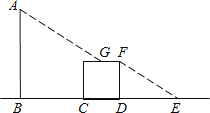
A、8 B、7 C、6 D、5二、填空题
-
9. 如图是小孔成像原理的示意图， ， ， . 若物体的高度为 ， 则像的高度是.
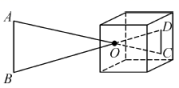10. 如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm．他准备了一支长为20cm的蜡烛，想要得到高度为5cm的像．蜡烛应放在距离纸筒 cm的地方．
11. 如图，身高为1.8米的某学生想测量学校旗杆的高度，当他站在B处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AB=2米，BC=18米，则旗杆CD的高度是米．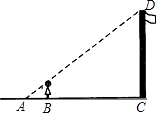
12. 如图①是用杠杆撬石头的示意图，当用力压杠杆时，杠杆绕着支点转动，另一端会向上撬起，石头就被撬动了．在图②中，杠杆的D端被向上撬起的距离BD＝8cm，动力臂OA与阻力臂OB满足OA＝3OB（AB与CD相交于点O），要把这块石头撬起，至少要将杠杆的C点向下压 cm．
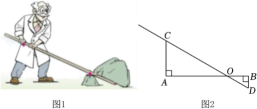13. 如图，在一场羽毛球比赛中，站在场内M处的运动员林丹把球从N点击到了对方内的B点，已知网高OA=1.52米，OB=4米，OM=5米，则林丹起跳后击球点N离地面的距离NM=米．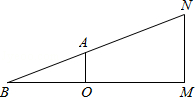
三、解答题
-
14. 小聪和他的同学利用影长测量旗杆高度(如图)，当1m长的直立竹竿的影长为1.5m时，测量旗杆落在地上的影长为21m，落在墙上的影长为2m．求旗杆的高度．
15.如图，为了估算河的宽度，我们可以在河对岸选定一个目标点P ， 在近岸取点Q和S ， 使点P、Q、S共线且直线PS与河垂直，接着再过点S且与PS垂直的直线a上选择适当的点T ， 确定PT与过点Q且垂直PS的直线b的交点R ． 如果测得QS=45m ， ST=90m ， QR=60m ， 求河的宽度PQ ．
16.如图，有一块三角形的土地，它的一条边BC=100米，BC边上的高AH=80米．某单位要沿着边BC修一座底面是矩形DEFG的大楼，D、G分别在边AB、AC上．若大楼的宽是40米（即DE=40米），求这个矩形的面积．
17. 如图，屋架跨度的一半 ， 高度 ． 现要在屋顶上开一个天窗，在水平位置，且 ． 求天窗高度的长．
18. “周末好去处，鳌山公园行”，鳌山公园的印鳌阁塔已成为市民常去的景点．某中学数学组进行综合实践活动，测量印鳌阁塔的高度．小彤同学在她与印鳌阁塔之间的地面上平放一面镜子，在镜子上做一个标记 ， 她看着镜子来回移动，直至看到印鳌阁塔顶端在镜子中的像与镜子上的标记重合．如图，此时测得 ， ， ， 求印鳌阁塔的高度．
19. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳，如图是小然站在地面欣赏悬挂在墙壁上的油画（）的示意图，设油画与墙壁的夹角 ， 此时小然的眼睛与油画底部处于同一水平线上，视线恰好落在油画的中心位置处，且与垂直．已知油画的长度为 ．
(1)、视线的度数为；（用含的式子表示）(2)、当小然到墙壁的距离时，求油画顶部点到墙壁的距离；(3)、当油画底部处位置不变，油画与墙壁的夹角逐渐减小时，小然为了保证欣赏油画的视觉效果最佳，他应该更靠近墙壁 ， 还是不动或者远离墙壁？（直接回答即可）20. 有一块三角形余料 ， 它的边 ， 高 ． 要把它加工成正方形零件，使正方形的一边在上，其余两个顶点分别在上．
(1)、问加工成的正方形零件的边长是多少？(2)、如果原题中要加工的零件是一个矩形，且此矩形是由两个并排放置的正方形所组成，如图1，此时，这个矩形零件的两条边长又分别为多少？请计算．