【培优版】北师大版数学九年级上册4.4探索三角形相似的条件 同步练习
试卷更新日期:2024-09-28 类型:同步测试
一、选择题
-
1. 如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F 在另一条直线上. 以下结论正确的是( )
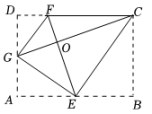 A、△COF∽△CEG B、OC=3OF C、AB:AD=4:3 D、GE=DF2. 如图,四边形 是边长为2的正方形点P为线段 上的动点,E为 的中点,射线 交 的延长线于点Q,过点E作 的垂线交 于点H.交 的延长线于点F,则以下结论:① ;② ;③当点F与点C重合时 ;④当 时, .成立的是( )
A、△COF∽△CEG B、OC=3OF C、AB:AD=4:3 D、GE=DF2. 如图,四边形 是边长为2的正方形点P为线段 上的动点,E为 的中点,射线 交 的延长线于点Q,过点E作 的垂线交 于点H.交 的延长线于点F,则以下结论:① ;② ;③当点F与点C重合时 ;④当 时, .成立的是( ) A、①②③ B、①③④ C、②③④ D、②④3. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )
A、①②③ B、①③④ C、②③④ D、②④3. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )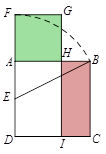 A、
A、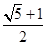 B、
B、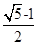 C、
D、1
4. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
C、
D、1
4. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ) A、(6,5) B、(6,0) C、(6,4) D、(4,2)5. 在中, , 用直尺和圆规在AB上确定点D , 使 , 根据作图痕迹判断,正确的是( )A、
A、(6,5) B、(6,0) C、(6,4) D、(4,2)5. 在中, , 用直尺和圆规在AB上确定点D , 使 , 根据作图痕迹判断,正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在中,点D,E分别是 , 上的点,与交于点F,下列条件中不能使和相似的是( )
6. 如图,在中,点D,E分别是 , 上的点,与交于点F,下列条件中不能使和相似的是( ) A、 B、 C、 D、7.
A、 B、 C、 D、7.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
 A、4或4.8 B、3或4.8 C、2或4 D、1或68. 如图正方形 , 点分别在边上,且 , 把绕点沿逆时针方向旋转得到 , 连接交于点 , 连接 , 并在上截取 , 连接 , 有如下结论:①;②始终平分;③;④;⑤垂直平分 , 上述结论中,所有正确的个数是( )
A、4或4.8 B、3或4.8 C、2或4 D、1或68. 如图正方形 , 点分别在边上,且 , 把绕点沿逆时针方向旋转得到 , 连接交于点 , 连接 , 并在上截取 , 连接 , 有如下结论:①;②始终平分;③;④;⑤垂直平分 , 上述结论中,所有正确的个数是( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
9. 在平面直角坐标系xOy中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C , 延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第1个正方形的面积为;第n个正方形的面积为 .
 10. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .11. 如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为时,△ADP和△ABC相似.
10. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .11. 如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为时,△ADP和△ABC相似.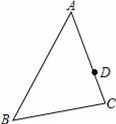 12. 如图,在正方形网格中有三个三角形,分别是 , , , 其中与相似的是 .
12. 如图,在正方形网格中有三个三角形,分别是 , , , 其中与相似的是 .
三、解答题
-
13. 如图,在菱形ABCD中,P是它对角线上面的一个点,连接CP后并延长,交CD于点E , 交BA的延长线于点F .
 (1)、求证:∠DCP=∠DAP;(2)、如果PE=4,EF=7,求线段PC的长.14. 巴台农神庙的设计代表了古希腊建筑艺术上的最高水平,它的平面图可看作宽与长的比是的矩形,我们将这种宽与长的比是的矩形叫黄金矩形.如图①,已知黄金矩形的宽 .
(1)、求证:∠DCP=∠DAP;(2)、如果PE=4,EF=7,求线段PC的长.14. 巴台农神庙的设计代表了古希腊建筑艺术上的最高水平,它的平面图可看作宽与长的比是的矩形,我们将这种宽与长的比是的矩形叫黄金矩形.如图①,已知黄金矩形的宽 .
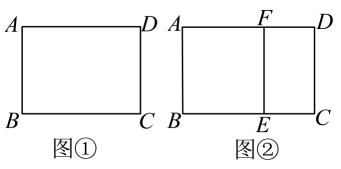 (1)、黄金矩形的长 ;(2)、如图②,将图①中的黄金矩形裁剪掉一个以为边的正方形 , 得到新的矩形 , 猜想矩形是否为黄金矩形,并证明你的结论;(3)、在图②中,连接 , 求点到线段的距离.15. 如图,在中,、为边上的两个动点, .
(1)、黄金矩形的长 ;(2)、如图②,将图①中的黄金矩形裁剪掉一个以为边的正方形 , 得到新的矩形 , 猜想矩形是否为黄金矩形,并证明你的结论;(3)、在图②中,连接 , 求点到线段的距离.15. 如图,在中,、为边上的两个动点, . (1)、若 , , 则与相似吗?为什么?(2)、若即、重合 , 则时,∽;(3)、当和满足怎样的数量关系时,∽?请说明理由.16. 再读教材:宽与长的比是(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形(提示:MN=2).
(1)、若 , , 则与相似吗?为什么?(2)、若即、重合 , 则时,∽;(3)、当和满足怎样的数量关系时,∽?请说明理由.16. 再读教材:宽与长的比是(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形(提示:MN=2).第-步:在矩形纸片一端利用图①的方法折出一个正方形,然后把纸片展平.

第二步:如图②,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步:折出内侧矩形的对角线AB , 并把AB折到图③中所示的AD处.

第四步:展平纸片,按照所得的点D折出DE , 使DE⊥ND , 则图④中就会出现黄金矩形.
问题解决:
(1)、图③中,AB=(保留根号).(2)、如图③,判断四边形BADQ的形状,并说明理由.(3)、在图④中,直接写出所有黄金矩形.17. 如图,△ABC 中,∠C=90°,AC=3cm,BC=4cm,动点 P 从点 B 出发以 2cm/s 速度向点C移动,同时动点 Q 从 C 出发以 1cm/s 的速度向点 A 移动, 设它们的运动时间为 t. (1)、根据题意知:CQ= , CP=;(用含 t 的代数式表示)(2)、t 为何值时,△CPQ 的面积等于△ABC 面积的 ?(3)、运动几秒时,△CPQ 与△CBA 相似?18. 如图
(1)、根据题意知:CQ= , CP=;(用含 t 的代数式表示)(2)、t 为何值时,△CPQ 的面积等于△ABC 面积的 ?(3)、运动几秒时,△CPQ 与△CBA 相似?18. 如图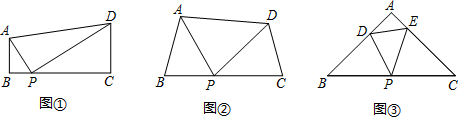 (1)、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)(2)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(3)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,则DE的长为 .19. 如图1,矩形ABCD中,点E为AB边上的动点(不与A,B重合),把 沿DE翻折,点A的对应点为 ,延长 交直线DC于点F,再把 折叠,使点B的对应点 落在EF上,折痕EH交直线BC于点H.
(1)、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)(2)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(3)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,则DE的长为 .19. 如图1,矩形ABCD中,点E为AB边上的动点(不与A,B重合),把 沿DE翻折,点A的对应点为 ,延长 交直线DC于点F,再把 折叠,使点B的对应点 落在EF上,折痕EH交直线BC于点H.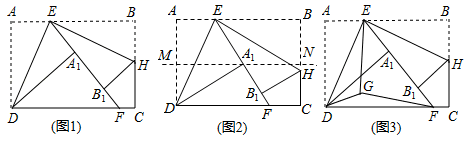 (1)、求证: ;(2)、如图2,直线MN是矩形ABCD的对称轴,若点 恰好落在直线MN上,试判断 的形状,并说明理由;(3)、如图3,在(2)的条件下,点G为 内一点,且 ,试探究DG,EG,FG的数量关系.
(1)、求证: ;(2)、如图2,直线MN是矩形ABCD的对称轴,若点 恰好落在直线MN上,试判断 的形状,并说明理由;(3)、如图3,在(2)的条件下,点G为 内一点,且 ,试探究DG,EG,FG的数量关系.