【提升版】北师大版数学九年级上册 4.4探索三角形相似的条件 同步练习
试卷更新日期:2024-09-28 类型:同步测试
一、选择题
-
1. 如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
 A、
A、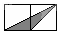 B、
B、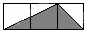 C、
C、 D、
D、 2. “黔绣”的技师擅长在叶脉上飞针走绣,巧妙地将传统刺绣图案与树叶天然纹理完美结合,创作出神奇的“叶脉苗绣”作品.实际上,很多叶片本身都蕴含着黄金分割的比例,在大自然中呈现出优美的样子.如图,点P大致是的黄金分割点 , 如果的长为 , 那么的长约为( )
2. “黔绣”的技师擅长在叶脉上飞针走绣,巧妙地将传统刺绣图案与树叶天然纹理完美结合,创作出神奇的“叶脉苗绣”作品.实际上,很多叶片本身都蕴含着黄金分割的比例,在大自然中呈现出优美的样子.如图,点P大致是的黄金分割点 , 如果的长为 , 那么的长约为( ) A、 B、 C、 D、3. 在学习画线段AB的黄金分割点时,小明过点B作AB的垂线BC,取AB的中点M,以点B为圆心,BM为半径画弧交射线BC于点D,连接AD,再以点D为圆心,DB为半径画弧,前后所画的两弧分别与AD交于E,F两点,最后,以A为圆心,“■■”的长度为半径画弧交AB于点H,点H即为AB的其中一个黄金分割点, 这里的“■■”指的是线段( )
A、 B、 C、 D、3. 在学习画线段AB的黄金分割点时,小明过点B作AB的垂线BC,取AB的中点M,以点B为圆心,BM为半径画弧交射线BC于点D,连接AD,再以点D为圆心,DB为半径画弧,前后所画的两弧分别与AD交于E,F两点,最后,以A为圆心,“■■”的长度为半径画弧交AB于点H,点H即为AB的其中一个黄金分割点, 这里的“■■”指的是线段( ) A、AF B、DF C、AE D、DE4. 如图,在中,为锐角, , , 要在边上找一点 , 使 , 需添加一个条件,下列方案不正确的是( )
A、AF B、DF C、AE D、DE4. 如图,在中,为锐角, , , 要在边上找一点 , 使 , 需添加一个条件,下列方案不正确的是( ) A、 B、 C、平分 D、5. 如图,在△ABC纸片中,∠A=72°,∠B=38°.将△ABC纸片沿某直线剪开,下列四种方式中剪下的阴影三角形与△ABC相似的是( )
A、 B、 C、平分 D、5. 如图,在△ABC纸片中,∠A=72°,∠B=38°.将△ABC纸片沿某直线剪开,下列四种方式中剪下的阴影三角形与△ABC相似的是( ) A、①② B、②④ C、③④ D、①③6. 如图,已知 , 那么添加一个条件后,依然无法判定∽( )
A、①② B、②④ C、③④ D、①③6. 如图,已知 , 那么添加一个条件后,依然无法判定∽( ) A、 B、 C、 D、7. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足 , 则称点P是AB的黄金分割点,世界上最有名的建筑物中几乎都包含“黄金分割”,若图中AB=8,则BP的长度是( )
A、 B、 C、 D、7. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足 , 则称点P是AB的黄金分割点,世界上最有名的建筑物中几乎都包含“黄金分割”,若图中AB=8,则BP的长度是( ) A、 B、 C、 D、28. 下列条件中,能使△ABC和△DEF相似的条件是( ).A、AB=c,AC=b,BC=a,DE= , EF= , DF= B、AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1 C、AB=3,AC=4,BC=6,DE=12,EF=8,DF=6 D、AB= , AC= , BC= , DE= , EF=3,DF=3
A、 B、 C、 D、28. 下列条件中,能使△ABC和△DEF相似的条件是( ).A、AB=c,AC=b,BC=a,DE= , EF= , DF= B、AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1 C、AB=3,AC=4,BC=6,DE=12,EF=8,DF=6 D、AB= , AC= , BC= , DE= , EF=3,DF=3二、填空题
-
9. 如图,乐器上的一根弦 , 两个端点A , B固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点A的黄金分割点,C , D之间的距离为 .
 10. 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD如图所示,点N在边AD上,现将矩形折叠,折痕为BN,点A对应的点记为点M,若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是 .
10. 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD如图所示,点N在边AD上,现将矩形折叠,折痕为BN,点A对应的点记为点M,若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是 . 11. 五角星是我们常见的图形,如图点 , 分别是线段的黄金分割点, , 则 .
11. 五角星是我们常见的图形,如图点 , 分别是线段的黄金分割点, , 则 . 12. 如图,在正方形网格上,若使 , 则点P应在 .
12. 如图,在正方形网格上,若使 , 则点P应在 .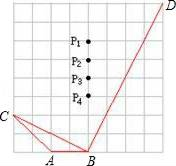 13. 如图,在△ABC中,AB=8 cm,BC=16 cm.点P从点A出发,沿AB边向点B以2cm/s的速度运动,点Q从点B出发,沿BC边向点C以4 cm/s的速度运动.如果P,Q分别从A,B同时出发,那么运动时间为时,△PBQ与△ABC相似.
13. 如图,在△ABC中,AB=8 cm,BC=16 cm.点P从点A出发,沿AB边向点B以2cm/s的速度运动,点Q从点B出发,沿BC边向点C以4 cm/s的速度运动.如果P,Q分别从A,B同时出发,那么运动时间为时,△PBQ与△ABC相似.
三、解答题
-
14. 如图,矩形中, , 点M是的中点,连接 . 将沿着折叠后得 , 延长交于E , 连接 .
 (1)、求证:平分;(2)、求证:△EMC∽△MAB.15. 如图,AD⊥AB,BC⊥AB,垂足分别为A,B,且AD=2,BC=6,AB=7.P是线段AB上的一个动点.问:是否存在一点P,使以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似?若存在,求出PA的长;若不存在,请说明理由.
(1)、求证:平分;(2)、求证:△EMC∽△MAB.15. 如图,AD⊥AB,BC⊥AB,垂足分别为A,B,且AD=2,BC=6,AB=7.P是线段AB上的一个动点.问:是否存在一点P,使以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似?若存在,求出PA的长;若不存在,请说明理由. 16. 如图,在的正方形方格纸中(每个小方格的边长均为1)有线段AC和EF , 点A , C , E , F均在方格的格点上.
16. 如图,在的正方形方格纸中(每个小方格的边长均为1)有线段AC和EF , 点A , C , E , F均在方格的格点上. (1)、在方格纸中画出一个以AC为对角线的菱形ABCD , 点D在直线AC的下方,且点B , D都在方格的格点上;(2)、在方格纸中画出以EF为边的正方形EFGH , 且点G , H在方格的格点上;(3)、连接BD交AC于点O , 连线得和 , 请证明 .17. 如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
(1)、在方格纸中画出一个以AC为对角线的菱形ABCD , 点D在直线AC的下方,且点B , D都在方格的格点上;(2)、在方格纸中画出以EF为边的正方形EFGH , 且点G , H在方格的格点上;(3)、连接BD交AC于点O , 连线得和 , 请证明 .17. 如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动. (1)、经过几秒△PCQ的面积为△ACB的面积的 ?(2)、经过几秒,△PCQ与△ACB相似?18. 在四边形中,为对角线, , 于点E, , .
(1)、经过几秒△PCQ的面积为△ACB的面积的 ?(2)、经过几秒,△PCQ与△ACB相似?18. 在四边形中,为对角线, , 于点E, , . (1)、如图1,求证:;(2)、如图2,延长 , 交边的延长线于点F,交边于点G,连接 , 在不添加任何字母和辅助线的条件下,请直接写出图中与相似,但不全等的三角形.19. 如图
(1)、如图1,求证:;(2)、如图2,延长 , 交边的延长线于点F,交边于点G,连接 , 在不添加任何字母和辅助线的条件下,请直接写出图中与相似,但不全等的三角形.19. 如图 (1)、如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值 叫做AE与AB的黄金比.)(2)、如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(1)、如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值 叫做AE与AB的黄金比.)(2)、如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
20. 【问题提出】已知有两个Rt△ABC和Rt△A'B′C',其中∠C=∠C′=90°,∠A=60°,∠A′=45°. (1)、如图1,作线段CD,C′D′,分别交AB于点D,交A'B′于点D′,使得∠BCD=45°,∠B'C′D'=30°,问△BCD与△B'C′D',△ACD与△A′C′D′是否相似?并选择其中相似的一对三角形,说明理由.(2)、如图2,作线段AD,B'D′,分别交BC于点D,交A'C'于点D,若△ACD与△B′C′D′、△ABD与△A′B'D'均相似,求∠CAD,∠C'B'D′的度数.(3)、【拓展思考】已知任意两个不相似的直角三角形,能否分别作一条直线对其进行分割,使其中一个三角形所分割得到的两个三角形与另一个三角形所分割得到的两个三角形分别对应相似?如果可以,请直接画出一种分割示意图;如果不能,请说明理由.
(1)、如图1,作线段CD,C′D′,分别交AB于点D,交A'B′于点D′,使得∠BCD=45°,∠B'C′D'=30°,问△BCD与△B'C′D',△ACD与△A′C′D′是否相似?并选择其中相似的一对三角形,说明理由.(2)、如图2,作线段AD,B'D′,分别交BC于点D,交A'C'于点D,若△ACD与△B′C′D′、△ABD与△A′B'D'均相似,求∠CAD,∠C'B'D′的度数.(3)、【拓展思考】已知任意两个不相似的直角三角形,能否分别作一条直线对其进行分割,使其中一个三角形所分割得到的两个三角形与另一个三角形所分割得到的两个三角形分别对应相似?如果可以,请直接画出一种分割示意图;如果不能,请说明理由.