【基础版】北师大版数学九年级上册 4.4探索三角形相似的条件 同步练习
试卷更新日期:2024-09-28 类型:同步测试
一、选择题
-
1. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
 A、
A、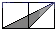 B、
B、 C、
C、 D、
D、 2. 如图,能使∽成立的条件是( )
2. 如图,能使∽成立的条件是( )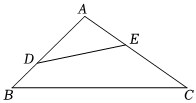 A、 B、 C、 D、3. 黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法,其原理是:如图,将正方形ABCD的底边BC取中点E,以E为圆心,线段DE为半径作圆,其与底边BC的延长线交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形,若CF=4a,则AB=( ).
A、 B、 C、 D、3. 黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法,其原理是:如图,将正方形ABCD的底边BC取中点E,以E为圆心,线段DE为半径作圆,其与底边BC的延长线交于点F,这样就把正方形ABCD延伸为矩形ABFG,称其为黄金矩形,若CF=4a,则AB=( ). A、(﹣1)a B、(2﹣2)a C、(+1)a D、(2+2)a4. 如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:① , ② , ③ , ④ , ⑤ , 使与一定相似的有( )
A、(﹣1)a B、(2﹣2)a C、(+1)a D、(2+2)a4. 如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:① , ② , ③ , ④ , ⑤ , 使与一定相似的有( )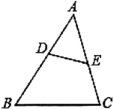 A、①②④ B、②④⑤ C、①②③④ D、①②③⑤5. 一条线段的黄金分割点有( )A、1个 B、2个 C、3个 D、无数个6. 如图,在中,是的平分线,与交于点M , , 下列结论中正确的个数是( )
A、①②④ B、②④⑤ C、①②③④ D、①②③⑤5. 一条线段的黄金分割点有( )A、1个 B、2个 C、3个 D、无数个6. 如图,在中,是的平分线,与交于点M , , 下列结论中正确的个数是( )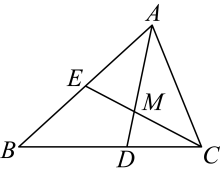
① ;② ;
③;④
A、1个 B、2个 C、3个 D、4个7. 已知是线段AB的黄金分割点),则下列结论中,正确的有( ).①;②;③
A、0个 B、1个 C、2个 D、3个8. 如图所示,四边形ABCD的对角线AC与BD相交于点 , 且 , 则①;②.下列关于①②的判断,正确的是( ). A、①②都正确 B、①正确,②错误 C、①错误,②正确 D、①②都错误
A、①②都正确 B、①正确,②错误 C、①错误,②正确 D、①②都错误二、填空题
-
9. 如图1,点把线段分成两条线段和 , 如果 , 那么称线段被点黄金分割,点叫做线段的黄金分割点.设 , , 则 , 所以 , 即叫做黄金比.一些美术家认为:人的上、下身长之比接近黄金比,可以增加美感.如图2的人体雕像高为 , 下身长为 , 为增加视觉美感,若图中为2米,则为米.
 10. 底角相等的两个等腰三角形相似.(填“一定”或“不一定”)11. 如图,要使图中的两个三角形相似,需要添加一个条件,这个条件可以是 . (写一个即可)
10. 底角相等的两个等腰三角形相似.(填“一定”或“不一定”)11. 如图,要使图中的两个三角形相似,需要添加一个条件,这个条件可以是 . (写一个即可) 12. 如图所示,点在的边AC上,若要使与相似,可添加的一个条件是.(只需写出一个)
12. 如图所示,点在的边AC上,若要使与相似,可添加的一个条件是.(只需写出一个)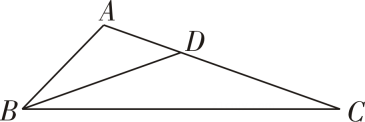 13. 已知点D是线段AB的黄金分割点,且线段AD的长为12厘米,则最短线段BD的长是.
13. 已知点D是线段AB的黄金分割点,且线段AD的长为12厘米,则最短线段BD的长是.三、解答题
-
14. 一个三角形的三边长分别为12cm,8cm,7cm,另一个三角形的三边长分别为16cm,24cm,14cm,这两个三角形相似吗?为什么?15. 如图所示,的三边长分别为 , 的三边长分別为.与是否相似?为什么?
 16. 人体上半身长和下半身长的黄金比为 , 这时人的身长比例看上去更美观.某演员的身长情况如图所示,她想通过穿高跟鞋使身长比例更美观,于是她购买了一双6厘米的高跟鞋.请依据“黄金比”判断这双高跟鞋的高度是偏高还是偏低?
16. 人体上半身长和下半身长的黄金比为 , 这时人的身长比例看上去更美观.某演员的身长情况如图所示,她想通过穿高跟鞋使身长比例更美观,于是她购买了一双6厘米的高跟鞋.请依据“黄金比”判断这双高跟鞋的高度是偏高还是偏低? 17. 如图,矩形ABCD中,AB=16,BC=8,点P为AB边上一动点,DP交AC于点Q.
17. 如图,矩形ABCD中,AB=16,BC=8,点P为AB边上一动点,DP交AC于点Q. (1)、求证:;(2)、当时,求的长.
(1)、求证:;(2)、当时,求的长.


