【培优版】北师大版数学九年级上册 4.3相似多边形同步练习

试卷更新日期：2024-09-28 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，一块矩形ABCD绸布的长AB=a，宽AD=1，按照图中的方式将它裁成相同的三面矩形彩旗，如果裁出的每面彩旗与矩形ABCD绸布相似，则a的值等于（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

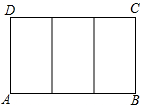查看试题解析
2. 如图，在长为8cm，宽为4cm的矩形中，截去一个矩形，使得留下的矩形（图中阴影部分）与原矩形相似，则留下的矩形的面积是（）

A、 $2 c m^{2}$ B、 $4 c m^{2}$ C、 $8 c m^{2}$ D、 $16 c m^{2}$

查看试题解析
3. 如图，小康利用复印机将一张长为 $5 c m$ ，宽为 $3 c m$ 的矩形图片放大，其中放大后的长为 $10 c m$ ，则放大后的矩形的面积为（）

A、 $60 c m^{2}$ B、 $58 c m^{2}$ C、 $45 c m^{2}$ D、 $30 c m^{2}$

查看试题解析
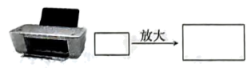4. 制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，则扩大后长方形广告牌的成本是（）

A、360元 B、720元 C、1080元 D、2160元

查看试题解析
5. 矩形相邻的两边长分别为25和 $x (x < 25)$ ，把它按如图所示的方式分割成五个全等的小矩形，每一个小矩形均与原矩形相似，则 $x$ 的值为（）

A、5 B、 $5 \sqrt{5}$ C、 $5 \sqrt{10}$ D、10

查看试题解析
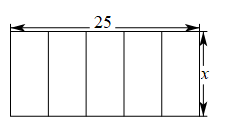6. 如图所示，一般书本的纸张是在原纸张多次对开得到的.矩形 $A B C D$ 沿 $E F$ 对开后，再把矩形 $E F C D$ 沿 $M N$ 对开，依此类推.若各种开本的矩形都相似，那么 $\frac{A B}{A D}$ 等于（）.

A、 $0.618$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、 $2$

查看试题解析
7. 如图，在矩形ABCD中，AB＝1，BC＝2，连接AC ，以对角线AC为边，按逆时针方向作矩形ACC₁B₁ ，使矩形ACC₁B₁∽矩形ADCB；再连接AC₁ ，以对角线AC₁为边，按逆时针方向作矩形AC₁C₂B₂ ，使矩形AC₁C₂B₂∽矩形ACC₁B₁ ， …，按照此规律作下去，则边AC₂₀₂₂的长为（　　）

A、 $\sqrt{5} \times {(\frac{\sqrt{5}}{2})}^{2022}$ B、 $2 \times {(\frac{\sqrt{5}}{2})}^{2021}$ C、 $\sqrt{5} \times 2^{2022}$ D、 $\sqrt{5} \times {(\frac{\sqrt{5}}{2})}^{2021}$

查看试题解析
8. 要拼出和图①中的菱形相似的较长对角线为88cm的大菱形(如图②) ，需要如图①的菱形的个数是（）．

A、11个 B、121个 C、22个 D、242 个

查看试题解析

二、填空题

9. 如图，矩形ABCD被分割为3个面积相等的小矩形，已知矩形AFED与原矩形ABCD相似，则原矩形的较长边与较短边的比值是．

查看试题解析
10. 如图，矩形ABCD中，AD=2，AB=4，剪去一个矩形AEFD后，余下的矩形EBCF∽矩形BCDA，则CF的长为。

查看试题解析
11. 一块矩形绸布的宽 $A B = 1 m$ ，长 $A D = a m$ ，按照图中所示的方式将它裁成相同的n面矩形彩旗，且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同，那么a的值应当是.

查看试题解析
12. 如图所示，一般书本的纸张是原纸张多次对开得到，矩形 $A B C D$ 沿 $E F$ 对开后，再把矩形 $E F C D$ 沿 $M N$ 对开，依次类推，若各种开本的矩形都相似，那么 $\frac{A D}{A B}$ 的值为．

查看试题解析
13. 八卦是中国文化的基本哲学概念，如图是八卦模型图，其制作要样板为图中的正八边形ABCDEFGH，已知八卦模型图的周长为10cm，在模型放大3倍的样板图中AB＋BC＋CD＋DE＝cm．

查看试题解析

三、解答题

14. 如图，要设计一本书的封面，封面长40cm，宽30cm，正中央是一个与整个封面长宽比例相同的矩形，如果要使四周边衬所占面积是封面面积的 $\frac{7}{16}$ ，且上、下边衬等宽，左、右边衬等宽，求上下边衬的宽.

查看试题解析
15. 如图，矩形ABCD的长AB=30，宽BC=20．

(1)、如图①，若矩形ABCD内四周有宽为1的方形区域，图中矩形ABCD与矩形A'B'C'D'相似吗？为什么？

(2)、如图②，当x为多少时，矩形ABCD和矩形A'B'C'D'相似？

查看试题解析
16.
如图，A_n系列矩形纸张的规格特征是：①各矩形纸张都相似；②A₁纸对裁后可以得到两张A₂纸，A₂纸对裁后可以得到两张A₃纸，…，A_n纸对裁后可以得到两张A_n+1纸．
（1）求：A₁纸面积是A₂纸面积的多少倍，A₂纸周长是A₄纸周长的多少倍；
（2）根据A_n系列纸张的规格特征，求出该系列纸张的长与宽（长大于宽）之比；
（3）设A₁纸张的重量为a克，试求出A₈纸张的重量．（用含a的代数式表示）

查看试题解析
17. 如图，四边形ABCD的顶点坐标分别是A(1，3)，B(1，1)，C(3，2)，D(2，3)．

(1)、将四边形ABCD各顶点的横坐标和纵坐标都乘2，得到一个新的四边形EFGH．在图中画出四边形EFGH．

(2)、从四边形ABCD到四边形EFGH属于什么图形变化？

(3)、对于这两个四边形，你能得出什么结论？请写出三条你认为正确的结论．

查看试题解析
18. 如图，把一个矩形 $A B C D$ 划分成三个全等的小矩形.

(1)、若原矩形 $A B C D$ 的长 $A B = 6$ ，宽 $B C = 4$ .问：每个小矩形与原矩形相似吗？请说明理由.

(2)、若原矩形的长 $A B = a$ ，宽 $B C = b$ ，且每个小矩形与原矩形相似，求矩形长 $a$ 与宽 $b$ 应满足的关系式.

查看试题解析
19. 某校九年级数学兴趣小组在探究相似多边形问题时，他们提出了下面两个观点：
观点一：将外面大三角形按图1的方式向内缩小，得到新三角形，它们对应的边间距都为1，则新三角形与原三角形相似.

观点二：将邻边为6和10的矩形按图2的方式向内缩小，得到新的矩形，它们对应的边间距都为1，则新矩形与原矩形相似.

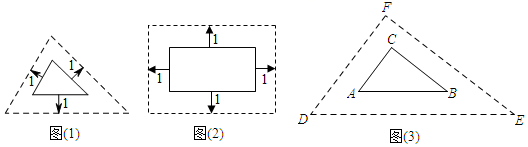
请回答下列问题：

(1)、你认为上述两个观点是否正确？请说明理由.

(2)、如图3，已知 $Δ A B C$ ，AC=6，BC=8，AB=10，将 $Δ A B C$ 按图3的方式向外扩张，得到 $Δ D E F$ ，它们对应的边间距都为1，DE=15，求 $Δ D E F$ 的面积.

查看试题解析
20. 阅读下列材料，完成任务：
自相似图形

定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形.例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形.

任务：

(1)、如图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为；

(2)、如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC，则△ACD与△ABC的相似比为；

(3)、现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）.
请从下列A、B两题中任选一条作答.

A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=（用含b的式子表示）；

②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=（用含n，b的式子表示）；

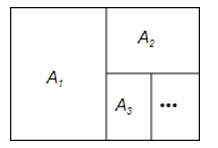
B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含b的式子表示）；

②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含m，n，b的式子表示）.

查看试题解析

【培优版】北师大版数学九年级上册 4.3相似多边形 同步练习

一、选择题

二、填空题

三、解答题

【培优版】北师大版数学九年级上册 4.3相似多边形同步练习