【培优版】北师大版数学九年级上册4.2平行线分线段成比例 同步练习
试卷更新日期:2024-09-28 类型:同步测试
一、选择题
-
1. 如图,H是△ABC的重心,延长AH交BC于D,延长BH交AC于M,E是DC上一点,且DE∶EC=5∶2,连结AE交BM于G,则BH∶HG∶GM等于( )
 A、7∶5∶2 B、13∶5∶2 C、5∶3∶1 D、26∶10∶32. 如图,在矩形 中, , , 平分 ,与对角线 相交于点N,F是线段 的中点,则 为( )
A、7∶5∶2 B、13∶5∶2 C、5∶3∶1 D、26∶10∶32. 如图,在矩形 中, , , 平分 ,与对角线 相交于点N,F是线段 的中点,则 为( ) A、 B、 C、 D、3. 如图,一人站在两等高的路灯之间走动, 为人 在路灯 照射下的影子, 为人 在路灯 照射下的影子.当人从点 走向点 时两段影子之和 的变化趋势是( )
A、 B、 C、 D、3. 如图,一人站在两等高的路灯之间走动, 为人 在路灯 照射下的影子, 为人 在路灯 照射下的影子.当人从点 走向点 时两段影子之和 的变化趋势是( ) A、先变长后变短 B、先变短后变长 C、不变 D、先变短后变长再变短4. AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
A、先变长后变短 B、先变短后变长 C、不变 D、先变短后变长再变短4. AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )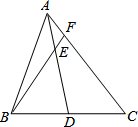 A、1:3 B、1:4 C、1:5 D、1:65. 如图,△ABC中,∠A=90°,AB=6,BC=10,∠ABC的平分线交AC于点D,与BC的垂线CE相交于点E,过点D作DF⊥BC于点F,则BD:DE为( )
A、1:3 B、1:4 C、1:5 D、1:65. 如图,△ABC中,∠A=90°,AB=6,BC=10,∠ABC的平分线交AC于点D,与BC的垂线CE相交于点E,过点D作DF⊥BC于点F,则BD:DE为( ) A、3:2 B、5:3 C、4:3 D、2:1
A、3:2 B、5:3 C、4:3 D、2:1二、填空题
-
6. 如图,矩形纸片ABCD,点E在边AD上,连接BE,点F在线段BE上,且EF=BF,折叠矩形纸片使点C恰好落在点F处,折痕为DG,若AB=4,则折痕DG的长为.
 7. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.将小正方形对角线EF双向延长,分别交边AB,和边BC的延长线于点G,H.若大正方形与小正方形的面积之比为5,GH=2 , 则大正方形的边长为 .
7. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.将小正方形对角线EF双向延长,分别交边AB,和边BC的延长线于点G,H.若大正方形与小正方形的面积之比为5,GH=2 , 则大正方形的边长为 . 8. 如图,正方形ABCD的边长AB=4,点E、F分别是CB,DC延长线上的点,连AF交CB于点G,若BE=1,连接AE,且∠EAF=45°,则AG长为.
8. 如图,正方形ABCD的边长AB=4,点E、F分别是CB,DC延长线上的点,连AF交CB于点G,若BE=1,连接AE,且∠EAF=45°,则AG长为.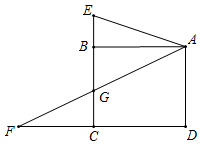 9. 如图,正方形中,E、F分别为、边的中点,连接 , 将正方形折叠,使点C落在上点P的位置,折痕交于点G , 若 , 则的长为.
9. 如图,正方形中,E、F分别为、边的中点,连接 , 将正方形折叠,使点C落在上点P的位置,折痕交于点G , 若 , 则的长为.
三、解答题
-
10. 如图,在中, , , , 动点从点出发,沿方向以每秒2个单位长度的速度向终点运动,点为线段的中点,过点向上作 , 且 , 以、为边作矩形 . 设点的运动时间为(t>0)秒.
 (1)、线段的长为(用含的代数式表示).(2)、当点N恰好落在边上时,求的值.(3)、当点在内部时,设矩形与重叠部分图形的面积为 , 求与之间的函数关系式.(4)、当点恰好落在的角平分线上时,直接写出的值.11. 已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明 成立(不要求考生证明).
(1)、线段的长为(用含的代数式表示).(2)、当点N恰好落在边上时,求的值.(3)、当点在内部时,设矩形与重叠部分图形的面积为 , 求与之间的函数关系式.(4)、当点恰好落在的角平分线上时,直接写出的值.11. 已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明 成立(不要求考生证明).若将图中的垂线改为斜交,如图,AB∥CD,AD,BC相交于点E,过点E作EF∥AB交BD于点F,则:
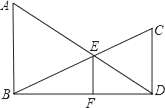
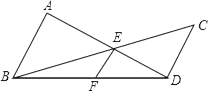 (1)、 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;(2)、请找出S△ABD , S△BED和S△BDC间的关系式,并给出证明.12. 阅读与计算,请阅读以下材料,完成相应的任务.
(1)、 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;(2)、请找出S△ABD , S△BED和S△BDC间的关系式,并给出证明.12. 阅读与计算,请阅读以下材料,完成相应的任务.材料:三角形的内角平分线定理:
如图1,在中,平分 , 交于点 , 则 .
下面是这个定理的部分证明过程.
证明:如图2,过作 , 交的延长线于点 .
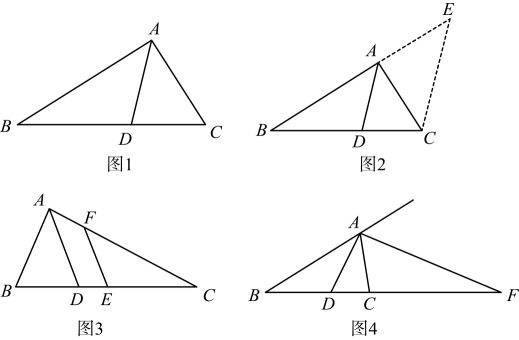 (1)、【思路说明】请按照上面的证明思路,写出该证明的剩余部分;(2)、【直接应用】如图3,中,是中点,是的平分线,交于 . 若 , , 求线段的长;(3)、【拓展延伸】如图4,中,平分 , 的延长线交外角角平分线于点 .
(1)、【思路说明】请按照上面的证明思路,写出该证明的剩余部分;(2)、【直接应用】如图3,中,是中点,是的平分线,交于 . 若 , , 求线段的长;(3)、【拓展延伸】如图4,中,平分 , 的延长线交外角角平分线于点 .①找出、、、这四条线段的比例关系,并证明;
②若 , , 求的长.

