【提升版】北师大版数学九年级上册 4.2平行线分线段成比例 同步练习
试卷更新日期:2024-09-28 类型:同步测试
一、选择题
-
1. 如图,直线 , 直线a , b相交于点 , 且与分别相交于点B , C和点D , E . 若 , , 则的长为( )
 A、 B、 C、 D、2. 如图是某景区大门部分建筑,已知 , , 当时,则的长是( )
A、 B、 C、 D、2. 如图是某景区大门部分建筑,已知 , , 当时,则的长是( ) A、 B、 C、 D、3. 如图,点是等边三角形的重心, , 是边上一点,当时,则的长为( )
A、 B、 C、 D、3. 如图,点是等边三角形的重心, , 是边上一点,当时,则的长为( ) A、1 B、 C、 D、24. 如图,若 , 则下列各式错误的是( )
A、1 B、 C、 D、24. 如图,若 , 则下列各式错误的是( ) A、 B、 C、 D、5. 如图, , , 则下列比例式不正确的是( )
A、 B、 C、 D、5. 如图, , , 则下列比例式不正确的是( ) A、 B、 C、 D、6. 如图,已知 , 它们依次交直线于点A、B、C和点D、E、F , 如果 , 那么的长等于( )
A、 B、 C、 D、6. 如图,已知 , 它们依次交直线于点A、B、C和点D、E、F , 如果 , 那么的长等于( ) A、2 B、4 C、 D、
A、2 B、4 C、 D、二、填空题
-
7. 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.点F是AB中点,连接CF,把线段CF沿射线BC方向平移到DE,点D在AC上.则线段CF在平移过程中扫过区域形成的四边形CFDE的面积为 .
 8. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点、、都在横格线上若线段 , 则线段 .
8. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点、、都在横格线上若线段 , 则线段 .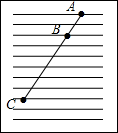 9. 如图,在中, , , 则 .
9. 如图,在中, , , 则 .
三、解答题
-
10. 如图, , 直线 , 交于点 , 且分别与直线 , , 交于点、、和点、、 , 已知 , , , , 求的长度是?
 11. 如图,在四边形ABCD中, , , , , .
11. 如图,在四边形ABCD中, , , , , . (1)、求证:四边形ABCD时菱形;(2)、延长BC至点M , 连接OM交CD于点N , 若 , 求 .12. 阅读下列材料,完成相应的任务:
(1)、求证:四边形ABCD时菱形;(2)、延长BC至点M , 连接OM交CD于点N , 若 , 求 .12. 阅读下列材料,完成相应的任务:我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使 .
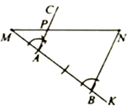
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使 ,连接BN;
③作射线 ,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵ (作法),∴
∵ (已知), (等量代换)
∵ (线段和差定义),∴ (等量代换,等式性质)
(1)、数学思考:
小颖作法理由中所缺的依据是:.(2)、拓展应用:
如图,已知线段a,b,c,求作线段d,使 a. B.
B.  C.
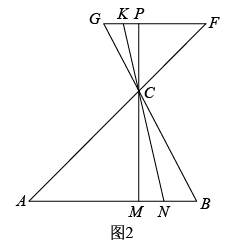
C.  13. 定义:如图1,点、把线段分割成三条线段、和 , 若 , 则称是线段的比例中段,、是线段的中段分点.
13. 定义:如图1,点、把线段分割成三条线段、和 , 若 , 则称是线段的比例中段,、是线段的中段分点. (1)、已知点、是线段的中段分点.
(1)、已知点、是线段的中段分点.①若 , , 则 ▲ ;
②在图1中,若 , , 求的长.
(2)、如图2,在中,是线段的比例中段,、分别是线段、延长线上的点,且 , 、的延长线分别交线段于点 , .探究是否为线段的比例中段,如果是,请给出证明,如果不是,请说明理由..