【培优版】北师大版数学九上4.1成比例线段同步练习

试卷更新日期：2024-09-28 类型：同步测试

进入出卷网下载

一、选择题

1. 已知abc $\neq$ 0，而且 $\frac{a + b}{c} = \frac{b + c}{a} = \frac{c + a}{b} = p$ ，那么直线y=px+p一定通过（）

A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限

查看试题解析
2. 若 $\frac{x + y}{y} = \frac{5}{3}$ ，则 $\frac{x}{y}$ 等于（）

A、 $\frac{3}{2}$ B、 $\frac{8}{3}$ C、 $\frac{2}{3}$ D、 $\frac{5}{8}$

查看试题解析
3. 下列线段a、b、c、d是成比例线段的是（）

A、 $a = 3$ ， $b = \sqrt{5}$ ， $c = \sqrt{15}$ ， $d = 2 \sqrt{3}$ B、 $a = 4$ ， $b = 6$ ， $c = 5$ ， $d = 10$ C、 $a = 12$ ， $b = 8$ ， $c = 15$ ， $d = 10$ D、 $a = \sqrt{2}$ ， $b = 3$ ， $c = 2$ ， $d = \sqrt{3}$

查看试题解析
4. 两地的实际距离是2000m，在地图上量得这两地的距离为2cm，这幅地图的比例尺是（）

A、1：1000000 B、1：100000 C、1：2000 D、1：1000

查看试题解析
5. 小丽和小强在阳光下行走，小强身高1.6米，他的影长2.0米，小强比小丽高10cm，此刻小丽的影长是（）

A、 $\frac{8}{15}$ 米 B、 $\frac{4}{15}$ 米 C、 $\frac{15}{4}$ 米 D、 $\frac{15}{8}$ 米

查看试题解析
6. 已知a，b，c为非零实数，且满足 $\frac{b + c}{a} = \frac{a + b}{c} = \frac{a + c}{b} = k$ ，则一次函数 $y = k x + 1 + k$ 的图象一定经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，一张矩形报纸ABCD的长AB=a，宽BC=b，E，F分别是AB，CD的中点．将这张报纸沿着直线EF对折后，矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比，则a：b等于（）．

A、 $\sqrt{2}$ ：1 B、1： $\sqrt{2}$ C、2：1 D、1：2

查看试题解析
8. 下列结论中，不正确的是（）

A、若 $\frac{a}{4} = \frac{c}{5}$ ，则 $\frac{a}{c} = \frac{4}{5}$ B、若 $\frac{a - b}{b} = \frac{1}{6}$ ，则 $\frac{a}{b} = \frac{7}{6}$ C、若 $\frac{a}{b} = \frac{c}{d} = \frac{2}{3}$ （b﹣d≠0），则 $\frac{a - c}{b - d} = \frac{2}{3}$ D、若 $\frac{a}{b} = \frac{3}{4}$ ，则a＝3，b＝4

查看试题解析

二、填空题

9. 已知 $\frac{a + b}{c}$ ＝ $\frac{a + c}{b}$ ＝ $\frac{b + c}{a}$ ＝k，则k的值是．

查看试题解析
10. 已知线段a，b，c，d成比例，且 $\frac{a}{b} = \frac{c}{d}$ ，其中a＝8cm，b＝4cm，c＝12cm，则d＝cm．

查看试题解析
11. 两把按不同比例尺标记刻度的尺子如图所示，每把尺子的刻度都是均匀的.已知两把尺子在刻度10处是对齐的，且上面的尺子在刻度13处与下面的尺子在刻度15处也刚好对齐，则上面尺子的刻度16在下面尺子对应的刻度是.

查看试题解析
12. 在芯片制作过程中，需要对 $A B = 2 cm ， A D = 3 cm$ 的矩形区域进行划区处理，划成如图所示的“ $M_{0} + N_{1}$ ” 的形式，其中 $M_{0}$ 为竖式矩形 $(\frac{A B}{A E} = \sqrt{2}) ， N_{1}$ 为横式矩形 $(\frac{E G}{E F} = \sqrt{2})$ ，则芯片被利用区域的长 $A G$ 的值为 cm .

查看试题解析
13. 如图，线段AB的长为1，C在AB上，D在AC上，且 $A C^{2} = B C \cdot A B$ ， $A D^{2} = C D \cdot A C$ ， $A E^{2} = D E \cdot A D$ ，则AE的长为．

查看试题解析

三、解答题

14. 已知 $a$ 、 $b$ 、 $c$ 是 $△ A B C$ 的三边，且满足 $\frac{a + 1}{3} = \frac{b - 4}{4} = \frac{c + 3}{8}$ ， $a + b + c = 30$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
15. 已知实数a、b、c满足 $\frac{a}{3} = \frac{b}{5} = \frac{c}{4}$ ，且 $a - 3 b + 2 c = - 8$ ．求： $\frac{a - 2 b}{2 c - 3 b}$ 的值．

查看试题解析
16. 如图，在线段AB上存在一点C，满足AC：CB=CB：AB=k．

(1)、求k的值．

(2)、若三条线段a，b，c满足a：b=b：c=k，问：这三条线段能否首尾相接构成一个三角形？如果能，指出三角形的形状；如果不能，请说明理由．

查看试题解析
17. 若a、b、c是非零实数，且满足 $\frac{a}{b + c} = \frac{b}{a + c} = \frac{c}{a + b} = k$ ，直线y=kx+b经过点（4，0），求直线y=kx+b与两坐标轴所围成的三角形的面积．

查看试题解析
18. 已知线段a，b，c满足 $\frac{a}{3} = \frac{b}{2} = \frac{c}{6}$ ，且a＋2b＋c＝26.

(1)、判断a，2b，c，b²是否成比例；

(2)、若实数x为a，b的比例中项，求x的值．

查看试题解析
19. 如图，在一块长为a(cm)，宽为b(cm)(a>b)的矩形黑板的四周，镶上宽为x(cm)的木板，得到一个新的矩形．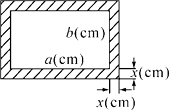

(1)、试用含a，b，x的代数式表示新矩形的长和宽；

(2)、试判断原矩形的长、宽与新矩形的长、宽是不是比例线段，并说明理由．

查看试题解析
20. 为了测得图甲和图乙中旗杆的高度，小明和小红在查阅资料后，得到一种测量旗杆高度的方法：找到旗杆的影子并找出其顶部，并在影子中间某处放置一竹竿，使得竹竿顶部的影子和旗杆顶部的影子重合，此时竹竿长度和竹竿影长之比即旗杆长度和旗杆影长之比.在太阳光下同一时刻小明和小红分别做了以上操作，测得竹竿CD长0.9m，其影长CE为1m.

(1)、如图甲所示，若小明测得旗杆影长AE为3m，求图甲中旗杆高AB为多少米.(CD⊥AE，AB⊥AE，点B，D，E在一条直线上)

(2)、如图乙所示，若小红测得旗杆落在地面上的影长FG为3m，落在墙上的影子GH的高为1.1m，则直接写出图乙中旗杆高FP为m.( $P F ⊥ F G ， H G ⊥ F G$ )

查看试题解析

【培优版】北师大版数学九上4.1成比例线段 同步练习

一、选择题

二、填空题

三、解答题

【培优版】北师大版数学九上4.1成比例线段同步练习