浙教版数学九上第3章圆的基本性质三阶单元测试卷

试卷更新日期：2024-09-28 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 如图，在 $△ A B C$ 中，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $68 °$ ， $B$ 和 $C$ 旋转后的对应点分别是 $B^{'}$ 和 $C^{'}$ ，连接 $B B^{'}$ ，则 $∠ A B B^{'}$ 的度数是( )

A、 $57 °$
B、 $54 °$
C、 $55 °$
D、 $56 °$

查看试题解析
2. 如图，在 $△ A B C$ 中， $A B = 3 \sqrt{2}, A C = 2$ ，以BC为边作 $R t △ B C D$ ， $B C = B D$ ，点D与点A在BC的两侧，则AD的最大值为（）

A、 $2 + 3 \sqrt{2}$ B、 $6 + 2 \sqrt{2}$ C、5 D、8

查看试题解析
3. 如图，小明荡秋千，位置从A点运动到了 $A^{'}$ 点，若 $∠ O A A^{'} = 55 °$ ，则秋千旋转的角度为（）

A、 $55 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
4. 如图，在折线段 $A - B - C$ 中， $A B = 10$ ， $B C = 3$ ，线段AB上有一点P ，将线段AB分成两个部分，分别以B点和P点为旋转中心旋转BC ， PA ．当BC ， BP ， PA三条线段首尾顺次相连构成等腰三角形时，BP的长是（）

A、3 B、5 C、3或5 D、3或5或7

查看试题解析
5. 如图所示，在四边形 $A B C D$ 中， $A C$ ， $B D$ 是对角线， $△ A B C$ 是等边三角形， $∠ A D C = 30 °$ ， $A D = 3$ ， $B D = 5$ ，则 $C D$ 的长为．（）

A、 $3 \sqrt{2}$ B、 $4$ C、 $2 \sqrt{5}$ D、 $4.5$

查看试题解析
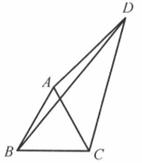6. 如图，直线 $E F$ 上有两点A、C ，分别引两条射线 $A B$ 、 $C D$ ． $∠ B A F = 100 °$ ， $C D$ 与 $A B$ 在直线 $E F$ 异侧．若 $∠ D C F = 60 °$ ，射线 $A B$ 、 $C D$ 分别绕A点，C点以1度/秒和6度/秒的速度同时顺时针转动，设时间为t秒，在射线 $C D$ 转动一周的时间内，当时间t的值为何时， $C D$ 与 $A B$ 平行（）

A、4或10秒 B、10或20秒 C、10或 40秒 D、4或40秒

查看试题解析
7. 如图，点 $O$ 在直线 $A B$ 上，过 $O$ 作射线 $O C$ ， $∠ B O C = 120 °$ ，一直角三角板的直角顶点与点 $O$ 重合，边 $O M$ 与 $O B$ 重合，边 $O N$ 在直线 $A B$ 的下方 $.$ 若三角板绕点 $O$ 按每秒 $10 °$ 的速度沿逆时针方向旋转一周，在旋转的过程中，第 $t$ 秒时，直线 $O N$ 恰好平分锐角 $∠ A O C$ ，则 $t$ 的值为（）

A、 $5$ B、 $6$ C、 $5$ 或 $23$ D、 $6$ 或 $24$

查看试题解析
8. 如图，在半圆 $A C B$ 中， $A B = 6$ ，将半圆 $A C B$ 沿弦 $B C$ 所在的直线折叠，若 $B C$ 恰好过圆心 $O$ ，则 $B C$ 的长是（）

A、 $3 \sqrt{3}$ B、 $π$ C、 $2 π$ D、 $4 π$

查看试题解析
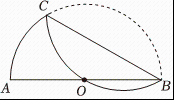9. 如图，点 E为正方形ABCD内一点， ∠AEB=90°，将△AEB绕点 B 按顺时针方向旋转90°，得到△CBG。延长AE交 CG于点 F，连接DE。下列结论： ①AF⊥CG，②四边形BEFG是正方形， ③若DA=DE，则2CF=CG； ④若△ADE是等边三角形，其中正确的结论是( )

A、①②③④ B、①②④ C、①③ D、①④

查看试题解析
10. 如图，一副三角板中两个直角顶点C叠放在一起，其中∠A=30°，∠B=60°，∠D=∠E=45°，保持三角板ABC不动，三角板DCE可绕点C旋转，则下列结论：①∠ACE=∠BCD；②∠BCE+∠ACD随着∠ACD的交化而变化；③当AB∥CE时，则∠ACD=60°或150°；④当∠BCE=3∠ACD时，DE一定垂直于AC．其中正确的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 如图， $P$ 是等边三角形 $A B C$ 内一点，将线段 $P B$ 绕点 $B$ 沿顺时针方向旋转60°得到线段 $B P ′$ ，连接 $C P ′$ ， $P P ′$ .若 $P B = 3$ ， $P C = 4$ ， $P A = 5$ ，则 $∠ B P C$ 的度数是.

查看试题解析
12. 对于平面直角坐标系xOy中的图形M和图形N ，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P ， Q两点间的距离有最小值，则称这个最小值为图形M ， N间的“捷径距离”，记为d（图形M ，图形N）．已知△ABC三个顶点的坐标分别为A（﹣2，1），B（﹣3，2），C（﹣1，2），将三角形ABC绕点D（a ， a）逆时针旋转90°得到△A^'B^'C^' ，若△A^'B^'C^'上任意点都在半径为4的⊙O内部或圆上，则△ABC与△A^'B^'C^'的“捷径距离”d（△ABC ， △A^'B^'C^'）的最小值是，最大值是．

查看试题解析
13. 如图，O是等边△ABC内一点，∠AOB＝105°，∠BOC＝α，将△BOC绕点C按顺时针方向旋转60°得到△ADC ，连接OD ．若△AOD是等腰三角形，则α的度数为．

查看试题解析
14. 如图，已知正方形ABCD的边长为6，点F是正方形内一点，连接EF ， DF ，且∠ADF＝∠DCF ，点E是AD边上一动点，连接EB ， EF ，则EB+EF长度的最小值为．

查看试题解析
15. 如图，在平面直角坐标系中，已知点 $A (- 3, 0)$ ， $B (0, 4)$ ， $A B = 5$ ，对三角形OAB连续做旋转变换，依次得到 $△_{1}$ ， $△_{2}$ ， $△_{3}$ ， ……，则 $△_{2024}$ 的直角顶点的纵坐标为．

查看试题解析
16. 如图，∠BAC=60°，∠ABC=45°，AB= $8 \sqrt{2}$ ， D是线段BC上的一个动点，以AD为直径画⊙O分别交AB ， AC于E ， F ，连接EF ，则线段EF长度的最小值为．

查看试题解析

三、解答题（本题共8小题，第17题8分，第18题6分，第19题6分，第20题6分，第21题6分，第22题12分，第23题10分，第24题12分，共66分）

17. 如图， $⊙ O$ 的直径 $A B$ 为 $10 cm$ ，弦 $A C$ 为 $6 cm$ ， $∠ A C B$ 的平分线交 $⊙ O$ 于点 $D$ ．

(1)、求 $A D$ 的长；

(2)、试探究 $C A 、 C B 、 C D$ 之间的等量关系，并证明你的结论；

(3)、连接 $O D$ ， $P$ 为半圆 $A D B$ 上任意一点，过 $P$ 点作 $P E ⊥ O D$ 于点 $E$ ，设 $△ O P E$ 的内心为 $M$ ，当点 $P$ 在半圆上从点 $B$ 运动到点 $A$ 时，求内心 $M$ 所经过的路径长．

查看试题解析
18. 如图，四边形ABCD内接于⊙O，C是 $\overset{⏜}{B D}$ 的中点，延长AB至点E，使得BE=AD，连结AC，CE.

(1)、求证：AC=CE.

(2)、若AD=4 $\sqrt{3}$ ， AB=6 $\sqrt{3}$ ， ∠BCD=120°，求BC的长。

查看试题解析
19. 如图，在每个小正方形的边长为 1 的网格中，等边三角形 $A B C$ 内接于圆，且顶点 $A ， B$ 均在格点上，若点 $D$ 在圆上， $A B$ 与 $C D$ 相交于点 $P$ ，请用无刻度的直尺，在如图所示的网格中，画出点 $Q$ ，使 $△ C P Q$ 为等边三角形，并简要说明点 $Q$ 的位置是如何找到的(不要求证明)

查看试题解析
20. 如图，在下列 $8 \times 8$ 的网格中，横、纵坐标均为整点的数叫做格点， $△ A B C$ 的顶点的坐标分别为 $A (3 ， 0)$ ， $B (0 ， 4)$ ， $C (4 ， 2)$ .

⑴直接写出 $△ A B C$ 的形状；

⑵要求在下图中仅用无刻度的直尺作图：将 $△ A B C$ 绕点 $B$ 逆时针旋转角度 $2 α$ 得到 $△ A_{1} B C_{1}$ ，其中 $α = ∠ A B C$ ， $A$ ， $C$ 的对应点分别为 $A_{1}$ ， $C_{1}$ ，请你完成作图；

⑶在网格中找一个格点 $G$ ，使得 $C_{1} G ⊥ A B$ ，并直接写出 $G$ 点的坐标；

⑷作点 $C_{1}$ 关于 $B C$ 的对称点 $D$ .

查看试题解析
21. 如图1， $▱ A B C D$ 绕点 $A$ 旋转得到平行四边形 $A E F G$ ，当点 $E$ 落在边 $C D$ 上时，连接 $B E$ ．

(1)、求证： $B E$ 平分 $∠ A E C$ ；

(2)、连接 $G B$ 交 $A E$ 于点 $M$ ．
①如图2，若平行四边形 $A B C D$ 为长方形，则 $G M$ 和 $B M$ 之间的等量关系为，并说明理由；
②如图3，若 $∠ B E C = 60 °, A B = 5, E C = 4$ ，请直接写出 $△ G A B$ 的面积．

查看试题解析
22. 数学老师在课堂上给出了一个问题，让同学们探究．在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，点D在直线BC上，将线段AD绕点A顺时针旋转60°得到线段AE ，过点E作EF∥BC ，交直线AB于点F ．

(1)、当点D在线段BC上时，如图①，求证：BD+EF＝AB；
分析问题：某同学在思考这道题时，想利用AD＝AE构造全等三角形，便尝试着在AB上截取AM＝EF ，连接DM ，通过证明两个三角形全等，最终证出结论：
推理证明：写出图①的证明过程：

(2)、探究问题：
当点D在线段BC的延长线上时，如图②：当点D在线段CB的延长线上时，如图③，请判断并直接写出线段BD ， EF ， AB之间的数量关系；

(3)、拓展思考：
在（1）（2）的条件下，若AC＝6 $\sqrt{3}$ ， CD＝2BD ，则EF＝．

查看试题解析
23. 如图 $1$ ， $△ A B C$ 内接于 $⊙ O$ ， $D$ 为 $B C$ 上一点，连接 $A D$ 、 $A O$ ， $∠ B A D = ∠ C A O$ ．

(1)、如图 $1$ ，求证： $A D ⊥ B C$ ；

(2)、如图 $2$ ，延长 $A D$ 交 $⊙ O$ 于点 $H$ ，连接 $C H$ ，若 $A B = 10$ ， $C H = 6$ ，求 $⊙ O$ 的半径．

查看试题解析
24. 已知正方形 $A B C D$ 中， $∠ M A N = 45 °$ ， $∠ M A N$ 绕点 $A$ 顺时针旋转，它的两边分别交 $C B$ ， $D C ($ 或它们的延长线 $)$ 于 $M$ ， $N$ ．

(1)、当 $∠ M A N$ 绕点 $A$ 旋转到 $B M = D N$ 时 $($ 如图 $1$ 所示 $)$ ，并将 $△ A B M$ 逆时针旋转 $90 °$ ，得到 $△ A B M^{'}$ ，求证 $B M + D N = M N$ ；

(2)、当 $∠ M A N$ 绕点 $A$ 旋转到 $B M \neq D N$ 时 $($ 如图 $2$ 所示 $)$ ，线段 $B M$ ， $D N$ 和 $M N$ 之间有怎样的数量关系？写出猜想，并加以证明；

(3)、当 $∠ M A N$ 绕点 $A$ 旋转到 $($ 如图 $3$ 所示 $)$ 的位置时，线段 $B M$ ， $D N$ 和 $M N$ 之间又有怎样的数量关系？请直接写出你的猜想．

查看试题解析

浙教版数学九上第3章 圆的基本性质 三阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题8分，第18题6分，第19题6分，第20题6分，第21题6分，第22题12分，第23题10分，第24题12分，共66分）

浙教版数学九上第3章圆的基本性质三阶单元测试卷