浙教版数学九上第3章 圆的基本性质 二阶单元测试卷
试卷更新日期:2024-09-28 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 在图形的平移和旋转变换中,下列说法正确的是( )A、对应点所连线段都平行 B、对应线段都平行 C、对应点所连线段都相等 D、对应线段都相等2. 如图,三角形OCD是由三角形OAB绕点O顺时针旋转40°后得到的图形,∠AOB=60°,则∠COB的度数是( )
 A、60° B、40° C、20° D、10°3. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=25°,则∠AOD等于( )
A、60° B、40° C、20° D、10°3. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=25°,则∠AOD等于( ) A、155° B、140° C、130° D、110°4. 如图, , 为的两条弦,连接 , , 若 , 则的度数为( )
A、155° B、140° C、130° D、110°4. 如图, , 为的两条弦,连接 , , 若 , 则的度数为( ) A、 B、 C、 D、5. 如图,正四边形ABCD和正五边形CEFGH内接于⊙O , AD和EF相交于点M , 则∠AMF的度数为( )
A、 B、 C、 D、5. 如图,正四边形ABCD和正五边形CEFGH内接于⊙O , AD和EF相交于点M , 则∠AMF的度数为( ) A、26° B、27° C、28° D、30°6. 如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB'C' . 点格点C'的坐标( )
A、26° B、27° C、28° D、30°6. 如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB'C' . 点格点C'的坐标( ) A、(0,4) B、(2,5) C、(0,﹣4) D、(﹣2,5)7. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点若 , 则的度数是用含的代数式表示
A、(0,4) B、(2,5) C、(0,﹣4) D、(﹣2,5)7. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点若 , 则的度数是用含的代数式表示 A、 B、 C、 D、8. 如图,在菱形中, , O为对角线的交点.将菱形绕点O逆时针旋转得到菱形 , 两个菱形的公共点为E , F , G , H.对八边形给出下面四个结论:
A、 B、 C、 D、8. 如图,在菱形中, , O为对角线的交点.将菱形绕点O逆时针旋转得到菱形 , 两个菱形的公共点为E , F , G , H.对八边形给出下面四个结论:
①该八边形各边长都相等;
②该八边形各内角都相等;
③点O到该八边形各顶点的距离都相等;
④点O到该八边形各边所在直线的距离都相等.
上述结论中,所有正确结论的序号是( )
A、①③ B、①④ C、②③ D、②④9. 如图,将两个全等的等腰直角三角形摆成如图所示的样子,其中 , , 、分别与交于D、E两点,将绕着点A顺时针旋转90°得到 , 则下列结论:①;②平分;③若 , 当时,则;④若平分 , 则 , 其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个10. 如图,在 中, , ,D,E分别为线段AB,AC上一点,且 ,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
A、1个 B、2个 C、3个 D、4个10. 如图,在 中, , ,D,E分别为线段AB,AC上一点,且 ,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
① ;②若 ,则 ;③若BE平分 ,则 ;④连结EF,若 ,则 .
A、①②③ B、③④ C、①②④ D、①②③④二、填空题(本题有6小题,每小题4分,共24分)
-
11. 如图所示,把绕点顺时针旋转 , 得到 , 交于点 , 若 , 则 .
 12. 如图,四边形ABCD为⊙O的内接四边形.若四边形ABCO为菱形,则∠ADC的大小为 .
12. 如图,四边形ABCD为⊙O的内接四边形.若四边形ABCO为菱形,则∠ADC的大小为 . 13. 如图,将边长为3的正方形ABCD绕点A逆时针方向旋转30°后得到正方形 , 则图中阴影部分面积为.
13. 如图,将边长为3的正方形ABCD绕点A逆时针方向旋转30°后得到正方形 , 则图中阴影部分面积为. 14. 如图,边长为的等边三角形中,是高上的一个动点,连接 , 同时将线段绕点顺时针旋转得到线段 , 连接 , 则点在运动的过程中,线段长度的最小值是 .
14. 如图,边长为的等边三角形中,是高上的一个动点,连接 , 同时将线段绕点顺时针旋转得到线段 , 连接 , 则点在运动的过程中,线段长度的最小值是 . 15. 如图,点A,B,C在⊙O上,四边形OABC是平行四边形,若对角线AC=2 , 则的长为 .
15. 如图,点A,B,C在⊙O上,四边形OABC是平行四边形,若对角线AC=2 , 则的长为 . 16. 如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD,把△ABC绕点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,则m=.
16. 如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD,把△ABC绕点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,则m=.
三、解答题(本题共8小题,第17题6分,第18题8分,第19题7分,第20题8分,第21题10分,第22题7分,第23题10分,第24题10分,共66分)
-
17. 如图,在正方形中,为的中点,连接 , 将绕点按逆时针方向旋转得到 , 连接 , 求的长.
 18. 如图,在长方形的网格中,每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,A,B,C均为格点.请你用一把无刻度直尺完成作图,保留作图痕迹.
18. 如图,在长方形的网格中,每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,A,B,C均为格点.请你用一把无刻度直尺完成作图,保留作图痕迹. (1)、以为旋转中心,将线段逆时针旋转至线段 , 连接;(2)、作于;(3)、将绕点顺时针旋转至 , 旋转角度等于 .19. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
(1)、以为旋转中心,将线段逆时针旋转至线段 , 连接;(2)、作于;(3)、将绕点顺时针旋转至 , 旋转角度等于 .19. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C, (1)、求证:CB∥PD;(2)、若BC=3,∠C=30°,求⊙O的直径.20. 【问题情境】
(1)、求证:CB∥PD;(2)、若BC=3,∠C=30°,求⊙O的直径.20. 【问题情境】
如图 , 点为正方形内一点, , 将绕点按顺时针方向旋转 , 得到点的对应点为点延长交于点 , 连接 .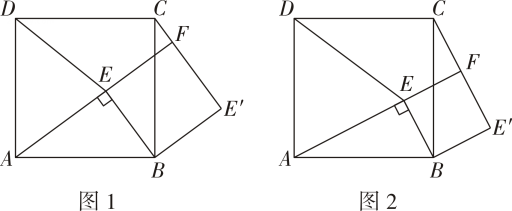 (1)、四边形的形状是 ;(2)、若 , , 则正方形的面积为 ;
(1)、四边形的形状是 ;(2)、若 , , 则正方形的面积为 ;
(3)、如图 , 若 , 请猜想线段与的数量关系并加以证明.21. 如图 ,正三角形、正方形、正六边形等正 边形与圆的形状有差异,我们将正 边形与圆的接近程度称为“接近度”. (1)、角的 “接近度” 定义:设正 边形的每个内角的度数为 , 将正 边形的 “接近度”定义为 . 于是 越小,该正 边形就越接近于圆.
(1)、角的 “接近度” 定义:设正 边形的每个内角的度数为 , 将正 边形的 “接近度”定义为 . 于是 越小,该正 边形就越接近于圆.①若 , 则该正 边形的 “接近度”等于.
②若 , 则该正 边形的“接近度”等于.
③当“接近度”等于时, 正 边形就成了圆.
(2)、边的 “接近度” 定义: 设一个正 边形的外接圆的半径为 , 正 边形的中心到各边的距离为 , 将正 边形的“接近度”定义为 . 分别计算当 时边的“接近度”, 并猜测当边的“接近度”等于多少时, 正 边形就成了圆.22. 如图,在菱形ABCD中,∠BAD>90°,P为AC,BD的交点,⊙O经过A,B,P三点. (1)、求证:AB为⊙O的直径,(2)、请用无刻度的直尺在圆上找一点Q,使得BP=PQ(不写作法,保留作图痕迹) .23. 如图 , 四边形是正方形, , 分别在边、上,且 , 我们称之为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图 , 将绕点顺时针旋转 , 点与点重合,得到 , 连接、、 .
(1)、求证:AB为⊙O的直径,(2)、请用无刻度的直尺在圆上找一点Q,使得BP=PQ(不写作法,保留作图痕迹) .23. 如图 , 四边形是正方形, , 分别在边、上,且 , 我们称之为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图 , 将绕点顺时针旋转 , 点与点重合,得到 , 连接、、 .
(1)、试判断 , , 之间的数量关系,并写出证明过程.
(2)、如图 , 点、分别在正方形的边、的延长线上, , 连接 , 请写出、、之间的数量关系,并写出证明过程.(3)、如图 , 在四边形中, , , , 点 , 分别在边 , 上, , 请直接写出线段 , , 之间数量关系.24. 如图,已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,AC=BD,AC⊥BD. (1)、猜想∠ACB的度数,并说明理由.(2)、若⊙O的半径为10,∠BCD=60°,求四边形ABCD的面积.(3)、若过圆心O作OF⊥BC于点F.求证:AD=2OF.
(1)、猜想∠ACB的度数,并说明理由.(2)、若⊙O的半径为10,∠BCD=60°,求四边形ABCD的面积.(3)、若过圆心O作OF⊥BC于点F.求证:AD=2OF.