浙教版数学九上第3章 圆的基本性质 一阶单元测试卷
试卷更新日期:2024-09-28 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 图中是圆心角的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A、2π B、4π C、12π D、24π3. 下列四幅图片中的主体事物,在现实运动中属于翻折的是( )A、
2. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A、2π B、4π C、12π D、24π3. 下列四幅图片中的主体事物,在现实运动中属于翻折的是( )A、 工作中的雨刮器
B、
工作中的雨刮器
B、 移动中的黑板
C、
移动中的黑板
C、 折叠中的纸片
D、
折叠中的纸片
D、 骑行中的自行车
4. 如图,在中,弦AB的长为8,圆心O到AB的距离 , 则的半径长为( )
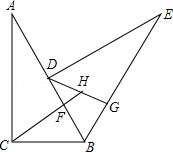
骑行中的自行车
4. 如图,在中,弦AB的长为8,圆心O到AB的距离 , 则的半径长为( ) A、4 B、 C、5 D、5. 如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是( )
A、4 B、 C、5 D、5. 如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是( ) A、42° B、21° C、84° D、60°6. 已知正多边形的一个内角是140°,则这个正多边形的边数是( )A、九 B、八 C、七 D、六7. 如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( )
A、42° B、21° C、84° D、60°6. 已知正多边形的一个内角是140°,则这个正多边形的边数是( )A、九 B、八 C、七 D、六7. 如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( ) A、30° B、40° C、50° D、60°8. 如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A、30° B、40° C、50° D、60°8. 如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( ) A、2-1 B、2 C、+ D、+29. 如图,在平面直角坐标系中,点A的坐标为(﹣4,0),点C的坐标为(0,2).以OA , OC为边作矩形OABC . 若将矩形OABC绕点O顺时针旋转90°,得到矩形OA'B'C' , 则点B'的坐标为( )
A、2-1 B、2 C、+ D、+29. 如图,在平面直角坐标系中,点A的坐标为(﹣4,0),点C的坐标为(0,2).以OA , OC为边作矩形OABC . 若将矩形OABC绕点O顺时针旋转90°,得到矩形OA'B'C' , 则点B'的坐标为( ) A、(﹣4,﹣2) B、(﹣4,2) C、(2,4) D、(4,2)10. 如图,在正方形中,为边上一点,点在边上,且 , 将点绕着点顺时针旋转 , 得到点 , 连接 , 则的最小值为( )
A、(﹣4,﹣2) B、(﹣4,2) C、(2,4) D、(4,2)10. 如图,在正方形中,为边上一点,点在边上,且 , 将点绕着点顺时针旋转 , 得到点 , 连接 , 则的最小值为( )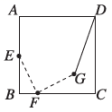 A、2 B、 C、3 D、
A、2 B、 C、3 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 已知四边形内接于 , 若 , 则的度数为.12. 半径为4,圆心角为的扇形的面积为(结果保留).13. 如图,四边形ABCD为平行四边形,以点A为圆心,AB长为半径画弧,交BC边于点E , 连接AE , AB=1,∠D=60°,则的长l=(结果保留π).
 14. 如图,△ABC内接于⊙O , AD是直径,若∠B=25°,则∠CAD=°.
14. 如图,△ABC内接于⊙O , AD是直径,若∠B=25°,则∠CAD=°. 15. 如图,将绕点顺时针旋转 , 得到 , 则 .
15. 如图,将绕点顺时针旋转 , 得到 , 则 . 16. 如图,抛物线与轴负半轴交于点A,P是以点为圆心,半径为2的圆上的动点,是线段PA的中点,连接OQ,则线段OQ的最小值是.
16. 如图,抛物线与轴负半轴交于点A,P是以点为圆心,半径为2的圆上的动点,是线段PA的中点,连接OQ,则线段OQ的最小值是.
三、解答题(本题共8小题,第17题6分,第18题6分,第19题6分,第20题7分,第21题7分,第22题11分,第23题11分,第24题12分,共66分)
-
17. 如图,在中, , 将线段绕点A逆时针旋转得到线段 , 过点D作 , 垂足为点E , , 求的度数.
 18. △ABC在平面直角坐标系xOy中的位置如图所示.
18. △ABC在平面直角坐标系xOy中的位置如图所示.
⑴作△ABC关于点C成中心对称的△A1B1C1 .
⑵将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2 .
⑶在x轴上求作一点P , 使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
19. 如图,已知点 , , 均在上,请用无刻度的直尺作图. (1)、如图1,若点是的中点,试画出的平分线;(2)、如图2,若 , 试画出的平分线.20. 综合与实践
(1)、如图1,若点是的中点,试画出的平分线;(2)、如图2,若 , 试画出的平分线.20. 综合与实践问题情境:“综合与实践”课上,老师提出如下问题:如图1,在中, , , , 将绕点A逆时针旋转得到 , 旋转角小于 , 点 B 的对应点为点D,点 C的对应点为点E,交于点O,延长交于点P.

数学思考:(1)试判断与的数量关系,并说明理由.
深入探究:(2)在以上图形旋转的过程中,老师让同学们提出新的问题.
① “乐学小组”提出问题:如图2,当时,则线段的长为 .
② “善思小组”提出问题:如图3,当时,求线段的长.
21. 【回顾课本】浙教版八年级下册数学教材“4.5三角形的中位线”一课中给出了“三角形的中位线定理”的证明思路,请完成证明过程.
已知:如图1,DE是△ABC的中位线.
求证:
分析:因为E是AC的中点,可以考虑以点E为中心,把△ADE按顺时针方向旋转180°,得到△CFE,这样就只需要证明四边形BCFD是平行四边形.
【探究发现】
如图2,等边△ABC的边长为2,点D,E分别为AB,AC边中点,点F为BC边上任意一点(不与B,C重合),沿DE,DF剪开分成①,②,③三块后,将②,③分别绕点D,E旋转180°恰好能与①拼成▱DIHG,求▱DIHG周长的最小值.
【拓展作图】
如图3,已知四边形ABCD,现要将其剪成四块,使得剪成的四块能通过适当的摆放拼成一个平行四边形,请在图3中画出剪痕,并对剪痕作适当的说明.
 22. 如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
22. 如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.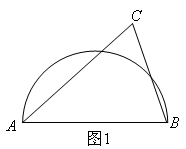
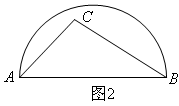 (1)、在图1中,画出△ABC的三条高的交点;(2)、在图2中,画出△ABC中AB边上的高.
(1)、在图1中,画出△ABC的三条高的交点;(2)、在图2中,画出△ABC中AB边上的高.