【培优版】浙教版数学九上4.6 相似多边形 同步练习
试卷更新日期:2024-09-28 类型:同步测试
一、选择题
-
1. 如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形 沿 对开后,再把矩形 沿 对开,依此类推.若各种开本的矩形都相似,那么 等于( ).
 A、 B、 C、 D、2. 如图,矩形ABCD的对称轴交AB于点E,交CD于点F.若矩形AEFD与矩形ABCD相似,则AB :BC的值为( )
A、 B、 C、 D、2. 如图,矩形ABCD的对称轴交AB于点E,交CD于点F.若矩形AEFD与矩形ABCD相似,则AB :BC的值为( ) A、2 B、 C、 D、3. 如图,已知矩形ABCD的边AD长为8cm,边AB长为6cm,从中截去一个矩形(图中阴影部分),如果所截矩形与原矩形相似,那么所截矩形的面积是( )
A、2 B、 C、 D、3. 如图,已知矩形ABCD的边AD长为8cm,边AB长为6cm,从中截去一个矩形(图中阴影部分),如果所截矩形与原矩形相似,那么所截矩形的面积是( )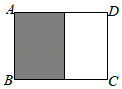 A、28cm2 B、27cm2 C、21cm2 D、20cm24. 如图所示,在矩形ABCD中, , 在BC上取一点 , 沿AE将向上折叠,使点落在AD上的点处,若四边形与矩形ABCD相似,则DF的长为( ).
A、28cm2 B、27cm2 C、21cm2 D、20cm24. 如图所示,在矩形ABCD中, , 在BC上取一点 , 沿AE将向上折叠,使点落在AD上的点处,若四边形与矩形ABCD相似,则DF的长为( ). A、 B、 C、 D、15. 如图所示,取一张长为、宽为的长方形纸片,将它对折两次后得到一张小长方形纸片.若要使小长方形与原长方形相似,则原长方形纸片的边a,b应满足的条件是( ).
A、 B、 C、 D、15. 如图所示,取一张长为、宽为的长方形纸片,将它对折两次后得到一张小长方形纸片.若要使小长方形与原长方形相似,则原长方形纸片的边a,b应满足的条件是( ). A、 B、 C、 D、6. 如图, 中, , 于D , 矩形、矩形的顶点分别在 , 的三边上,且矩形矩形 . 可求两矩形的相似比的是( )
A、 B、 C、 D、6. 如图, 中, , 于D , 矩形、矩形的顶点分别在 , 的三边上,且矩形矩形 . 可求两矩形的相似比的是( ) A、 B、 C、 D、7. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )
A、 B、 C、 D、7. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )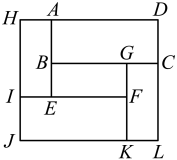 A、 B、 C、 D、8. 如图,用六个全等的直角三角形恰好拼成一大一小两个正六边形,则大正六边形与小正六边形的周长之比为( )
A、 B、 C、 D、8. 如图,用六个全等的直角三角形恰好拼成一大一小两个正六边形,则大正六边形与小正六边形的周长之比为( )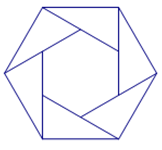 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
9. 如图,某校给初一年级划了一块大的矩形菜地,年级又将它分为大小形状完全相同的三块分给三个班,同学们测量后惊奇的发现,每块小菜地都与原大矩形菜地相似,则原矩形菜地的宽与长之比为 .
 10. 如图,在矩形中, , 点 , 分别是 , 边的中点,连接 , 若矩形与矩形相似,则矩形的面积为 .
10. 如图,在矩形中, , 点 , 分别是 , 边的中点,连接 , 若矩形与矩形相似,则矩形的面积为 .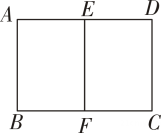 11. 如图,四边形四边形 , 若 , , , 则FG的长为 .
11. 如图,四边形四边形 , 若 , , , 则FG的长为 .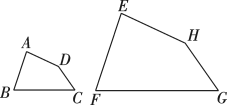 12. 制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是元.
12. 制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是元.三、解答题
-
13. 根据下列题目要求,解答下列问题:
 (1)、如图1,已知正方形ABCD和正方形BEFG,连接AG、CE.求证AG= CE.(2)、如图2,在矩形ABCD中,AB:BC=2:3,已知矩形ABCD∽矩形GBEF,相似比为AD:GF= , ∠ABG=30°,连接AG、CE,延长EF交BC于M.探究线段AG与CE的数量关系.(3)、如图3,已知矩形ABCD矩形GBEF,连接AG、CE、DF,发现线段AG、CE、DF存在这样的数量关系:AG2+CE2=DF2 , 请你对这个数量关系加以证明.
(1)、如图1,已知正方形ABCD和正方形BEFG,连接AG、CE.求证AG= CE.(2)、如图2,在矩形ABCD中,AB:BC=2:3,已知矩形ABCD∽矩形GBEF,相似比为AD:GF= , ∠ABG=30°,连接AG、CE,延长EF交BC于M.探究线段AG与CE的数量关系.(3)、如图3,已知矩形ABCD矩形GBEF,连接AG、CE、DF,发现线段AG、CE、DF存在这样的数量关系:AG2+CE2=DF2 , 请你对这个数量关系加以证明.四、实践探究题
-
14. 根据相似多边形的定义,我们把四个角分别相等、四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
 (1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确.
(1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确.命题①:各条边成比例的两个凸四边形相似.
命题②:三个角分别相等的两个凸四边形相似.
命题③:两个大小不同的正方形相似.
命题①为命题,命题②为命题,命题③为命题.(填“真”或“假”)
(2)、如图所示,在四边形ABCD和四边形中,.求证:四边形ABCD与四边形相似.
-