【提升版】浙教版数学九上4.6 相似多边形 同步练习
试卷更新日期：2024-09-28 类型：同步测试
一、选择题
-
1. 如图，一块矩形ABCD绸布的长AB=a，宽AD=1，按照图中的方式将它裁成相同的三面矩形彩旗，如果裁出的每面彩旗与矩形ABCD绸布相似，则a的值等于（ ）
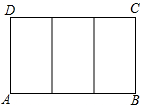A、 B、 C、2 D、2. 如图，在边长为1的正方形构成的网格中，四边形和四边形的相似比是（ ）
A、 B、 C、 D、3. 如图，在长为8cm，宽为4cm的矩形中，截去一个矩形，使得留下的矩形（图中阴影部分）与原矩形相似，则留下的矩形的面积是（ ）
A、 B、 C、 D、4. 如图四边形四边形 ， ， ， ， 则（ ）
A、4 B、5 C、8 D、105. 如图，小康利用复印机将一张长为 ， 宽为的矩形图片放大，其中放大后的长为 ， 则放大后的矩形的面积为（ ）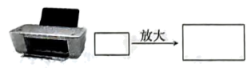
A、 B、 C、 D、6. 制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，则扩大后长方形广告牌的成本是（ ）A、360元 B、720元 C、1080元 D、2160元7. 如图，矩形ABCD∽矩形FAHG，连接BD，延长GH分别交BD、BC于点Ⅰ、J，延长CD、FG交于点E，一定能求出△BIJ面积的条件是（ ）
A、矩形ABJH和矩形HJCD的面积之差 B、矩形ABJH和矩形HDEG的面积之差 C、矩形ABCD和矩形AHGF的面积之差 D、矩形FBJG和矩形GJCE的面积之差8. 剪纸艺术是我国的非物质文化遗产，如图是以正八边形为背景图形设计成的剪纸作品，记正八边形的面积为 ， 图中阴影部分面积 ， 则的值为（ ）
A、 B、 C、 D、二、填空题
-
9. 已知两个相似多边形的面积比是9：16其中两个多边形的周长之差为8，则较小多边形的周长为.10. 如图，矩形ABCD被分割为3个面积相等的小矩形，已知矩形AFED与原矩形ABCD相似，则原矩形的较长边与较短边的比值是 ．
11. 如图，小莉用灯泡照射一个与墙面平行的矩形硬纸片ABCD，在墙上形成矩形影子 ． 现测得 ， ， 纸片ABCD的面积为 ， 则影子的面积为 ．
12. 如图，矩形ABCD中，AD=2，AB=4，剪去一个矩形AEFD后，余下的矩形EBCF∽矩形BCDA，则CF的长为。
三、解答题
-
13. 如图所示，E为矩形ABCD的BC边上一点，现将矩形沿AE翻折，点B的对应点F恰好落在AD上，且四边形FECD与原四边形相似.
(1)、求证：E为BC的黄金分割点.(2)、若矩形ABCD的面积为10，则四边形FECD的面积为多少?14. 如图所示，矩形AGFE∽矩形ABCD，AE，AD分别为它们的短边，点在AB上，.
(1)、求证：.(2)、若两个矩形的面积之和为 ， 求矩形ABCD的面积.四、实践探究题
-
15. 根据相似多边形的定义，我们把四个角分别相等、四条边成比例的两个凸四边形叫作相似四边形．相似四边形对应边的比叫作相似比．(1)、某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确(直接在横线上填写“真”或“假”)．
①四条边成比例的两个凸四边形相似；(命题)
②三个角分别相等的两个凸四边形相似；(命题)
③两个大小不同的正方形相似．(命题)
(2)、如图，在四边形ABCD和四边形A1B1C1D1中，∠ABC=∠A1B1C1 ， ∠BCD=∠B1C1D1 ， ， 求证：四边形ABCD与四边形A1B1C1D1相似．