【培优版】浙教版数学九上4.5 相似三角形的性质及应用同步练习

试卷更新日期：2024-09-28 类型：同步测试

进入出卷网下载

一、选择题

1. 如图．利用标杆BE测量建筑物的高度．已知标杆BE高1.2m ，测得AB＝1.6m ． BC＝12.4m ．则建筑物CD的高是（　　）

A、9.3m B、10.5m C、12.4m D、14m

查看试题解析
2. 如图，小明在A时测得某树的影长为 $8 m$ ， B时又测得该树的影长为 $2 m$ ，若两次日照的光线互相垂直，则树的高度为（）

A、 $2 m$ B、 $4 m$ C、 $6 m$ D、 $8 m$

查看试题解析
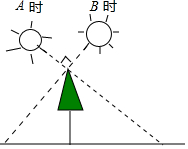3. 《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆AB ，从木杆的顶端B观察井水水岸D ，视线BD与井口的直径AC交于点E ，如果测得 $A B = 1$ 米， $A C = 1.6$ 米， $A E = 0.4$ 米，那么CD为（）米．

A、5 B、4 C、3 D、2

查看试题解析
4. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中第九卷，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”
译文：“今有一座长方形小城，东西向城墙长7里，南北向城墙长9里，各城墙正中均开一城门．走出东门15里处有棵大树，问走出南门多少步恰好能望见这棵树？”（注：1里 $= 300$ 步）你的计算结果是：出南门（）步而见木．

A、205 B、215 C、305 D、315

查看试题解析
5. 如图，某零件的外径为 $12 c m$ ，用一个交叉卡钳 $(A C = B D)$ 可测量零件的内孔直径 $A B .$ 若 $O A$ ： $O C = O B$ ： $O D = 2$ ，且量得 $C D = 5 c m$ ，则零件的厚度 $x$ 为（）

A、 $2 c m$ B、 $1.5 c m$ C、 $1 c m$ D、 $0.5 c m$

查看试题解析
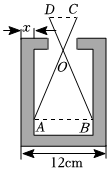6. “计里面方”（比例缩放和直角坐标网格体态）是中国古代地图制图的基本方法和数学基础，是中国古代地图独立发展的重要标志，制作地图时，人们会利用测杆、水准仪和照板来测量距离．在如图所示的测量距离 $A B$ 的示意图中，记照板“内芯”的高度为 $E F$ ，且 $E F ∥ A B$ ，观测者的眼睛（图中用点C表示）与 $B F$ 在同一水平线上，若某次测量中 $\frac{C F}{B F} = \frac{1}{5}$ ，则下列结论中错误的是（）

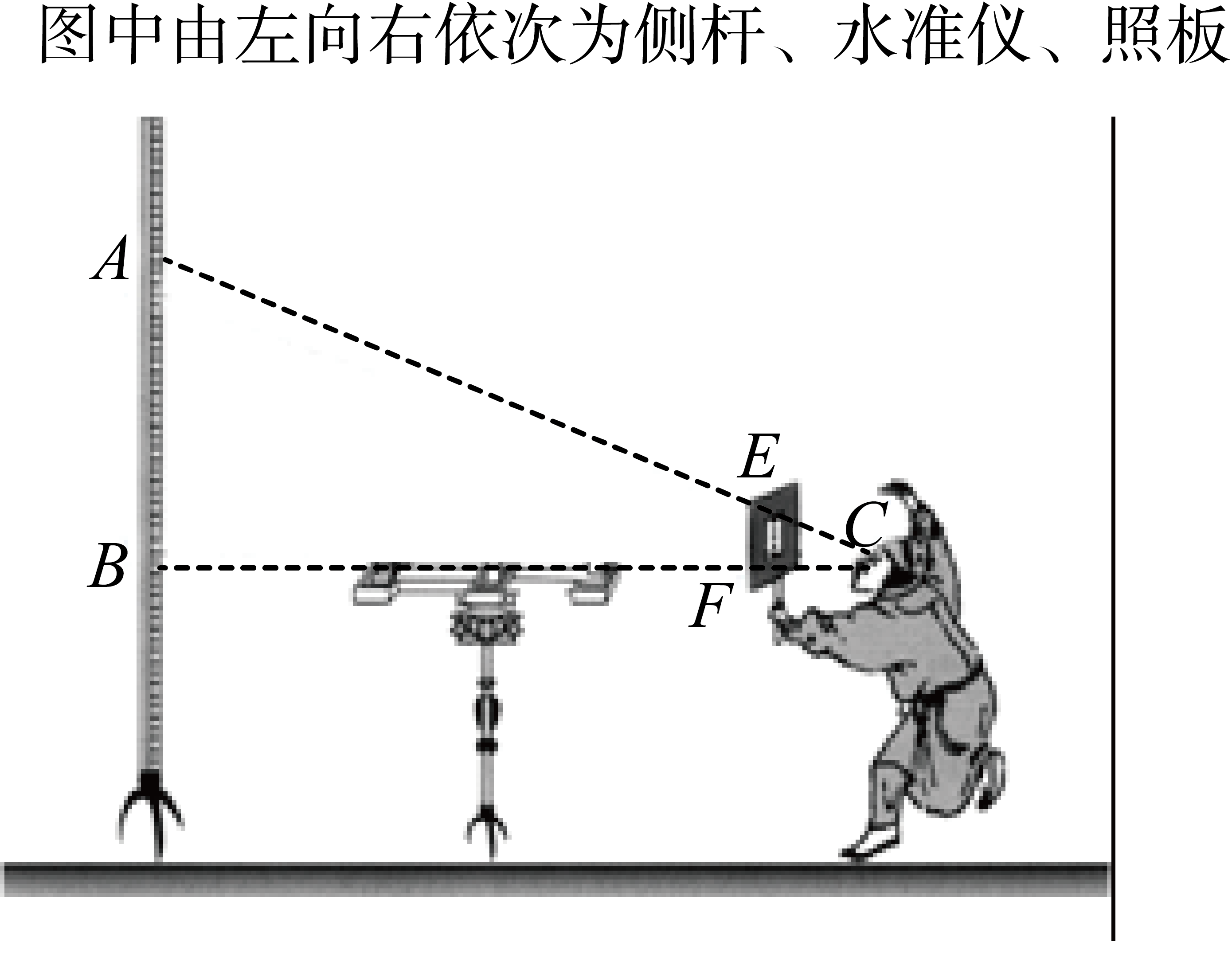A、 $\frac{C E}{A E} = \frac{1}{5}$ B、 $\frac{E F}{A B} = \frac{1}{6}$ C、 $\frac{C F}{C E} = \frac{1}{2}$ D、 $S_{△ C E F} ： S_{△ C A B} = 1 ： 36$

查看试题解析
7. 据《九章算术》记载：“今有山居木西，不知其高.山去五十三里，木高九丈五尺.人立木东三里，望木末适与山峰斜平.人目高七尺.问山高几何？”译文如下：如图，今有山 $A B$ 位于树的西面.山高 $A B$ 为未知数，山与树相距53里，树高9丈5尺.人站在离树3里的地方，观察到树梢C恰好与山峰A处在同一条直线上，人眼离地7尺.则山高 $A B$ 的长为（结果保留到整数，1丈=10尺）（）

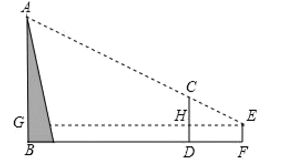A、162丈 B、163丈 C、164丈 D、165丈

查看试题解析
8. 《九章算术》中记载：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问邑方几何?”译文：一座正方形城池北、西边正中A，C处各开一道门(如图所示)，从点A处往正北方向走30步刚好有一棵树位于点 $B$ 处，若从点 $C$ 处往正西方向走750步到达点 $D$ 处时正好看到此树，则正方形城池的边长为（）.

A、300步 B、225步 C、150步 D、75步

查看试题解析

二、填空题

9. 《周髀算经》中记载了“偃矩以望高”的方法．“矩”在古代指两条边呈直角的曲尺（即图6中的 $A B C$ ）．“偃矩以望高”的意思是把“矩”仰立放，可测量物体的高度如图，点 $A$ ， $B$ ， $Q$ 在同一水平线上， $∠ A B C$ 和 $∠ A Q P$ 均为直角， $A P$ 与 $B C$ 相交于点 $D$ ．测得 $A B = 40 c m$ ， $B D = 20 c m$ ， $A Q = 12 m$ ，则树高 $P Q =$ ．

查看试题解析
10. 如图，这是小孔成像的示意图，光线经过小孔O ，物体AB在幕布上形成倒立的实像CD（点A ， B的对应点分别是C ， D）．若物体AB的高为 $6 c m$ ，实像CD的高度为 $4 c m$ ，则小孔O的高度OE为 $c m$ ．

查看试题解析
11. 公元前6世纪，古希腊学者泰勒斯曾用立杆测影的方法巧测金字塔的高度.如图，小明仿照这个方法，测量圆锥形小山包的高度，已知圆锥的底面周长为62.8m.先在小山包旁边立起一根木棒，当木棒影子长度等于木棒高度时，测得小山包影子AB的长为23m(直线AB过底面圆心)，则小山包的高为m(π取3.14).

查看试题解析
12. 我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？”．其大意是：如图，一座正方形城池，A为北门中点，从点A往正北方向走30步到B处有一树木，C为西门中点，从点C往正西方向走750步到D处正好看到B处的树木，则正方形城池的边长为步．

查看试题解析

三、解答题

13. 某校社会实践小组为了测量古塔的高度，在地面上C处垂直于地面竖立了高度为2米的标杆 $C D$ ，这时地面上的点E ，标杆的顶端点D ，古塔的塔尖点B正好在同一直线上，测得 $E C = 4$ 米，将标杆向后平移到点G处，这时地面上的点F ，标B杆的顶端点H ，古塔的塔尖点B正好在同一直线上（点F ，点G ，点E ，点C与古塔底处的点A在同一直线上），这时测得 $F G = 6$ 米， $C G = 20$ 米，请你根据以上数据，计算古塔的高度AB ．

查看试题解析

四、实践探究题

14.

探究不同裁剪方式的面积大小问题
素材1	图1是一张直角三角形纸板，两直角边分别为 $B C = 15 c m, A C = 20 c m$ ，小华、小明、小富同学分别用这样的纸板裁剪出不一样的矩形，并使矩形的四个顶点都在三角形的边上．
素材2	小华同学按图2的方式裁翦出一个正方形；小同学按图3的方式裁剪，且 $A H = 8 c m$ ．
素材3	小富同学对纸板的裁剪按如下步骤：如图4 步骤1：在直角 $△ A B C$ 纸板上裁下一个矩形 $C D E F$ ，矩形的四个顶点都在 $△ A B C$ 的边上；步骤2：取剩下的纸板 $△ A D E$ 裁下一个正方形GHJI，正方形的四个顶点都在 $△ A D E$ 边上；且满足矩形 $C D E F$ 的CF边长是正方形GHJI边长的两倍小0.9cm
问题解决
任务1	请比较小华、小明同学裁出的两种矩形的面积大小，通过计算说明.
任务2	请求出小富同学裁下的矩形CDEF各边长.

查看试题解析

15. 视力表中蕴含着很多数学知识，如：每个“E”形图都是正方形结构，同一行的“E”是全等图形且对应着同一个视力值，不同的检测距离需要不同的视力表．

(1)、素材1：国际通用的视力表以5米为检测距离，任选视力表中7个视力值n ，测得对应行的“E”形图边长b（mm），在平面直角坐标系中描点如图1．
探究1：检测距离为5米时，归纳n与b的关系式，并求视力值1.2所对应行的“E”形图边长．

(2)、素材2：图2为视网膜成像示意图，在检测视力时，眼睛能看清最小“E”形图所成的角叫做分辨视角，视力值与分辨视角（分）的对应关系近似满足 $n = \frac{1}{θ} (0.5 \leq θ \leq 10)$ ．
探究2：当 $n \geq 1.0$ 时，属于正常视力，根据函数增减性写出对应的分辨视角的范围．

(3)、素材3：如图3，当确定时，在A处用边长为 $b_{1}$ 的I号“E”测得的视力与在B处用边长为 $b_{2}$ 的Ⅱ号“E”测得的视力相同．
探究3：若检测距离为3米，求视力值1.2所对应行的“E”形图边长．

查看试题解析

16. 请阅读下列材料，完成相应的任务：

著名数学家华罗庚先生说过：“数缺形时少直观，形缺数时难入微，数形结合百般好，割裂分家万事休.”数形结合是数学研究和学习中的重要思想和解题方法，用数形结合方法可以使复杂问题简单化、抽象问题具体化，有助于把握数学问题的本质，解决更加广泛领域的问题．

比如有这样一个题目：设有两只电阻，分到为 $R_{1}$ 和 $R_{2}$ ，问并联后的电阻值 $R$ 是多少?

我们可以利用公式 $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ 求得 $R$ 的值，也可以设计一种图形直接得出结果，具体如下：如图①，在直线 $l$ 上任取两点A，B，分别过点A，B作直线 $l$ 的垂线，并在这两条垂线上分别截取 $A C = R_{1}, B D = R_{2}$ ，且点C，D位于直线 $l$ 的同侧，连接AD，BC，交于点 $E$ ，过点 $E$ 作 $E F ⊥$ 直线 $l$ ，则线段EF的长度就是并联后的电阻值 $R$ ．

证明： $∵ E F ⊥ l, C A ⊥ l$ ，

$∴ ∠ E F B = ∠ C A B = 9 0^{°}$ ，

又 $∵ ∠ E B F = ∠ C B A$ ，

$∴ △ E B F ~ △ C B A ($ 依据1），

$∴ \frac{B F}{A B} = \frac{E F}{A C}$ （依据2）．

同理可得： $: \frac{A F}{A B} = \frac{E F}{B D}$ ，

$∴ \frac{B F}{A B} + \frac{A F}{A B} = \frac{E F}{A C} + \frac{E F}{B D}$
∴ $I = \frac{E F}{A C} + \frac{E F}{B D}$ ，
∴ $\frac{1}{E F} = \frac{1}{A C} + \frac{1}{B D}$ ，
即： $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ .

(1)、上面证明过程中的“依据1”和“依据2”分别是谁：

依据1：.
依据2：.

(2)、如图②，两个电阻并联在同一电路中，已知R₁=3千欧，R₂=6千欧，请在图③中（1个单位长度代表1千欧）画出表示该电路图中总阻值R的线段长．

(3)、受以上作图法的启发，小明提出了已知R₁和R，求R₂的一种作图方法，如图④，作△ABC，使∠C=90°，AC=BC=R₁ ，过点B作BC的垂线，并在垂线上截取BD=R，使点D与点A在直线BC的同一侧，作射线AD，交CB的延长线于点E，则BE即为R₂ ．你认为他的方法是否正确，若正确，请加以证明；若不正确，请说明理由．