【提升版】浙教版数学九上4.5 相似三角形的性质及应用 同步练习
试卷更新日期：2024-09-27 类型：同步测试
一、选择题
-
1. 如图，小星用铅笔尖可以支起一张均匀的三角形硬纸板，他支起的这个点是三角形的( )
A、三条中线的交点 B、三条高所在直线的交点 C、三条角平分线的交点 D、三边垂直平分线的交点2. 凸透镜成像的原理如图所示，.若物体到焦点的距离与焦点到凸透镜中心线的距离之比为 ， 则物体被缩小到原来的（ ）
A、 B、 C、 D、3. 如图，某内空零件的外径为12cm，用一个交叉卡钳可测量零件的内孔直径AB. ， 量得 ， 若此零件外围材质厚度均匀，则零件的厚度为（ ）
A、2cm B、1.5cm C、1cm D、0.5cm4. 大约在两千四五百年前，墨子和他的学生做了世界上第1个小孔成倒像的实验（如图），解释了小孔成倒像的原理，并在《墨经》中有这样的记录：“景到，在午有端，与景长，说在端”．物理课上，小明记录了他和同桌所做的小孔成像实验数据（如图）：物距为 ， 像距为 ， 蜡烛火焰倒立的像的高度是 ， 则蜡烛火焰的高度是（ ）．
A、 B、 C、 D、5. 某数学兴趣小组为了估算河的宽度，在河对岸选定一个目标点P，在近岸取点Q和S，使点P、Q、S共线且直线PS与河垂直，接着在过点S且与PS垂直的直线a上选择适当的点T，确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m，ST=90m，QR=60m，则河的宽度PQ为（ ）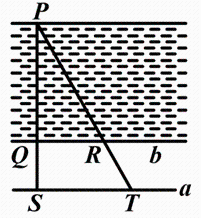
A、30m B、60m C、90m D、120m6. 四分仪是一种十分古老的测量仪器． 其出现可追溯到数学家托勒密的《天文学大成》． 图 1 是古代测量员用四分仪测量一方井的深度， 将四分仪置于方井上的边沿， 通过窥衡杆测望井底点 、窥衡杆与四分仪的一边 交于点 ． 图 2 中， 四分仪为正方形 ， 方井为矩形 ． 若测量员从四分仪中读得 为 为 0.5 ， 实地测得 为 2.5 ， 则井深 为（ ）
A、4 B、5 C、6 D、77. 图1是伸缩折叠不锈钢晾衣架的实物图，图2是它的侧面示意图，AD和CB相交于点O ， A ， B之间的距离为1.2米，AB∥CD ， 根据图2中的数据可得点C ， D之间的距离为（ ）
A、0.8米 B、0.86米 C、0.96米 D、1米8. 如图，为驾驶员的盲区，驾驶员的眼睛点处与地面 的距离为米，车头近似看成一个矩形，且满足 ， 若盲区的长度是米， 则车宽的长度为（ ）米.
A、 B、 C、 D、二、填空题
-
9. 利用相机的“微距模式”可以拍摄得到与实际物体等大或比实际物体稍大的图象，如图是一个微距拍摄成像的示意图，若拍摄远的物体 ， 其在底片上的图象的宽是 ， 焦距是 ， 则物体的宽是 ．
10. 某项目学习小组为了测量直立在水平地面上的旗杆 的高度， 把标杆 直立在同一水平地面上 （如图 ）． 同一时刻测得旗杆和标杆在太阳光下的影长分别是 ． 已知 ， 在同一条直线上， ， 则 m．
11. 在《数书九章》（宋·秦九韶）中记载了一个测量塔高的问题：如图所示，表示塔的高度，表示竹竿顶端到地面的高度，表示人眼到地面的高度，、、在同一平面内，点A、C、E在一条水平直线上．已知米，米，米，米，人从点F远眺塔顶B，视线恰好经过竹竿的顶端D，可求出塔的高度．根据以上信息，塔的高度为米．
12. 如图，在长沙一小区内拐角处的一段道路上，有一小朋友在C处玩耍，一辆汽车从被楼房遮挡的拐角另一侧的A处驶来（ ， ， 与相交于点O），已知米，米，米，米，则汽车从A处前行的距离米时，才能发现C处的小朋友．
三、解答题
-
13. 如图1所示的是古代一种可以远程攻击的投石车，图2是投石车投石过程中某时刻的示意图，GP是杠杆，弹袋挂在点G，重锤挂在点P，点A为支点，点D是水平底板BC上的一点，米，米.
(1)、投石车准备时，点G恰好与点B重合，此时AG和AC垂直，求AG(2)、投石车投石瞬间，AP的延长线交线段DC于点E，若DE：CE=5：1，则点G的上升高度为米.14. 为测量水平操场上旗杆的高度，九（2）班各学习小组运用了多种测量方法．
(1)、如图1，小张在测量时发现，自己在操场上的影长恰好等于自己的身高 ． 此时，小组同学测得旗杆的影长为 ， 据此可得旗杆高度为m；(2)、如图2，小李站在操场上E点处，前面水平放置镜面C ， 并通过镜面观测到旗杆顶部A ． 小组同学测得小李的眼睛距地面高度 ， 小李到镜面距离 ， 镜面到旗杆的距离 ． 求旗杆高度；(3)、小王所在小组采用图3的方法测量，结果误差较大．在更新测量工具，优化测量方法后，测量精度明显提高，研学旅行时，他们利用自制工具，成功测量了江姐故里广场雕塑的高度．方法如下：
如图4，在透明的塑料软管内注入适量的水，利用连通器原理，保持管内水面M ， N两点始终处于同一水平线上．
如图5，在支架上端P处，用细线系小重物Q ， 标高线始终垂直于水平地面．
如图6，在江姐故里广场上E点处，同学们用注水管确定与雕塑底部B处于同一水平线的D ， G两点，并标记观测视线与标高线交点C ， 测得标高 ， ． 将观测点D后移到处，采用同样方法，测得 ， ． 求雕塑高度（结果精确到）．
15. 学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．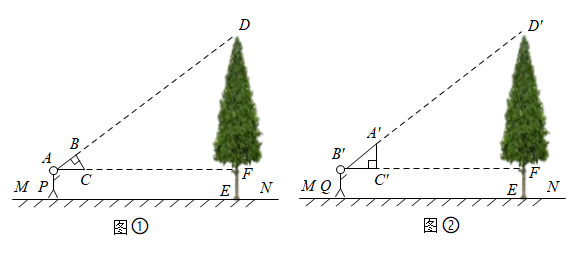
(1)、小丽先调整自己的位置至点 ， 将直角三角形纸板的三个顶点位置记为、、（如图①），斜边平行于地面（点、、、在一直线上），且点在边（较长直角边）的延长线上，此时测得边距离地面的高度为1.5米，小丽与古树的距离为16米，求古树的高度；(2)、为了尝试不同的思路，小丽又向前移动自己的位置至点 ， 将直角三角形纸板的三个顶点的新位置记为、、（如图②），使直角边（较短直角边）平行于地面（点、、、在一直线上），点在斜边的延长线上，且测得此时边距离地面的高度依然是1.5米，那么小丽向前移动了多少米？