【培优版】浙教版数学九上4.4 两个三角形相似的判定 同步练习
试卷更新日期:2024-09-27 类型:同步测试
一、选择题
-
1. 如图,点是□ABCD的边BA延长线上一点,连接CE,交边AD于点F,则下列各式正确的是( )
 A、 B、 C、 D、2. 如图,的顶点在第一象限内,边在轴正半轴上,点为原点,反比例函数交于点 , 交于点 , 且点为中点, , 若的面积为14,则的值为( )
A、 B、 C、 D、2. 如图,的顶点在第一象限内,边在轴正半轴上,点为原点,反比例函数交于点 , 交于点 , 且点为中点, , 若的面积为14,则的值为( ) A、 B、 C、 D、3. 如图,一块矩形木板 , 长 , 宽 , 小虎将一块等腰直角三角板的一条直角边靠在顶点上,另一条直角边与边交于点 , 三角板的直角顶点在边上移动(不含端点),当线段最短时,的长为( )
A、 B、 C、 D、3. 如图,一块矩形木板 , 长 , 宽 , 小虎将一块等腰直角三角板的一条直角边靠在顶点上,另一条直角边与边交于点 , 三角板的直角顶点在边上移动(不含端点),当线段最短时,的长为( ) A、 B、 C、 D、4. 在中, , , , 为边一点且 , 若过点作直线截 , 使截得的三角形与原三角形相似,则满足条件的直线有( )A、条 B、条 C、条 D、条5. 如图,在矩形中,以A为圆心,长为半径画圆弧,交于点E , 以E为圆心长为半径画圆弧与的延长线交于点F , 连接分别与、交于点M、N , 连接 , 下列结论中下列结论中错误的是( )
A、 B、 C、 D、4. 在中, , , , 为边一点且 , 若过点作直线截 , 使截得的三角形与原三角形相似,则满足条件的直线有( )A、条 B、条 C、条 D、条5. 如图,在矩形中,以A为圆心,长为半径画圆弧,交于点E , 以E为圆心长为半径画圆弧与的延长线交于点F , 连接分别与、交于点M、N , 连接 , 下列结论中下列结论中错误的是( ) A、四边形为菱形 B、 C、 D、6. 如图,在△ABC中,点D是AB上一点(不与点A , B重合),过点D作DE∥BC交AC于点E , 过点E作EF//AB交BC于点F , 点G是线段DE上一点,EG=2DG , 点H是线段CF上一点,CH=2HF , 连接AG , AH , GH , HE. 若已知△AGH的面积,则一定能求出( )
A、四边形为菱形 B、 C、 D、6. 如图,在△ABC中,点D是AB上一点(不与点A , B重合),过点D作DE∥BC交AC于点E , 过点E作EF//AB交BC于点F , 点G是线段DE上一点,EG=2DG , 点H是线段CF上一点,CH=2HF , 连接AG , AH , GH , HE. 若已知△AGH的面积,则一定能求出( ) A、△ABC的面积 B、△ADE的面积 C、四边形DBFE的面积 D、△EFC的面积7. 如图,四个全等的直角三角形排成“赵爽弦图”,其中四边形ABCD与四边形EFGH都是正方形.连结DG并延长,交BC于点 , 点为BC的中点.若 , 则AE的长为( )
A、△ABC的面积 B、△ADE的面积 C、四边形DBFE的面积 D、△EFC的面积7. 如图,四个全等的直角三角形排成“赵爽弦图”,其中四边形ABCD与四边形EFGH都是正方形.连结DG并延长,交BC于点 , 点为BC的中点.若 , 则AE的长为( ) A、4 B、 C、 D、8. 如图,在△ABC纸板中,AC=4,BC=8,AB=10,P是BC上一点,沿过点P的直线剪下一个与△ABC
A、4 B、 C、 D、8. 如图,在△ABC纸板中,AC=4,BC=8,AB=10,P是BC上一点,沿过点P的直线剪下一个与△ABC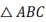 相似的小三角形纸板.针对CP的不同取值,三人的说法如下.下列判断正确的是( )
相似的小三角形纸板.针对CP的不同取值,三人的说法如下.下列判断正确的是( )甲:若CP=4,则有3种不同的剪法;乙:若CP=2,则有4种不同的剪法;
丙:若CP=1,则有3种不同的剪法.
 A、只有甲错 B、只有乙错 C、只有丙错 D、甲、乙、丙都对
A、只有甲错 B、只有乙错 C、只有丙错 D、甲、乙、丙都对二、填空题
-
9. 如图,在四边形ABCD中,连接AC , BD交于点E , 已知BE=CE , AB=AD , ∠ECB=2∠ABD , 若BD=16,AC=11,则边AB的长为 .
 10. 如图所示,点A1 , A2 , A3在x轴上且OA1=A1A2=A2A3 , 分别过点A1 , A2 , A3作y轴的平行线与反比例函数y(k>0,x>0)的图象分别交于点B1 , B2 , B3 , 分别过点B1 , B2 , B3作x轴的平行线分别与y轴交于点C1 , C2 , C3 , 连接OB1 , OB2 , OB3 , 那么图中阴影部分的面积之和为 .
10. 如图所示,点A1 , A2 , A3在x轴上且OA1=A1A2=A2A3 , 分别过点A1 , A2 , A3作y轴的平行线与反比例函数y(k>0,x>0)的图象分别交于点B1 , B2 , B3 , 分别过点B1 , B2 , B3作x轴的平行线分别与y轴交于点C1 , C2 , C3 , 连接OB1 , OB2 , OB3 , 那么图中阴影部分的面积之和为 . 11. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .
11. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .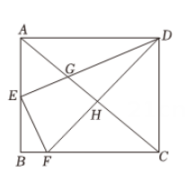 12. 如图,正比例函数的图象与反比例函数的图象交于A , B两点,过点A的直线分别与x轴、y轴交于C , D两点.当 , 时,则 .
12. 如图,正比例函数的图象与反比例函数的图象交于A , B两点,过点A的直线分别与x轴、y轴交于C , D两点.当 , 时,则 .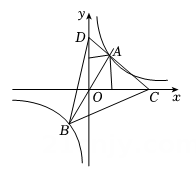 13. 如图,△ABC的面积为2,AD为BC边上的中线,点A , C1 , C2 , C3是线段CC4的五等分点,点A , D1 , D2是线段DD3的四等分点,点A是线段BB1的中点.
13. 如图,△ABC的面积为2,AD为BC边上的中线,点A , C1 , C2 , C3是线段CC4的五等分点,点A , D1 , D2是线段DD3的四等分点,点A是线段BB1的中点. (1)、△AC1D1的面积为;(2)、△B1C4D3的面积为 .
(1)、△AC1D1的面积为;(2)、△B1C4D3的面积为 .三、解答题
-
14. 矩形ABCD中,M , N分别是边AB , BC上的两个动点.
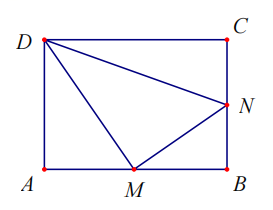 (1)、如图,当 DM⊥ MN , AM=BM时. 求证:①△DAM∽△MBN;②DN=AD+BN.(2)、当 AB=5,BC=3 时,是否存在点 M的某个位置,使得△DAM∽△MBN∽△DCN ,
(1)、如图,当 DM⊥ MN , AM=BM时. 求证:①△DAM∽△MBN;②DN=AD+BN.(2)、当 AB=5,BC=3 时,是否存在点 M的某个位置,使得△DAM∽△MBN∽△DCN ,若存在,求 AM的长. 若不存在,说明理由.
(3)、是否存在矩形 ABCD , 使得△DAM , △MBN , △DCN都和△DMN相似,若存在,求 的值;若不存在,请说明理由.15. 如图1,在中, , , 点P为AB上一点, , 过点P作交AC于点Q点P , Q的距离为 , 的周长与的周长之比为. (1)、请直接写出 , 分别关于x的函数表达式,并注明自变量x的取值范围;(2)、在给定的平面直角坐标系中,画出函数 , 的图象,并分别写出函数 , 的一条性质;(3)、结合函数图象,请直接写出时x的取值范围(近似值保留小数点后一位,误差不超过0.2).
(1)、请直接写出 , 分别关于x的函数表达式,并注明自变量x的取值范围;(2)、在给定的平面直角坐标系中,画出函数 , 的图象,并分别写出函数 , 的一条性质;(3)、结合函数图象,请直接写出时x的取值范围(近似值保留小数点后一位,误差不超过0.2).四、实践探究题
-
16. 【教材呈现】如图是华师版九年级上册数学教材第77页的部分内容.

猜想:如图,在△ABC中,点D、E分别是AB与AC的中点.根据画出的图形,可以猜想:
DE∥BC , 且DE=BC
对此,我们可以用演绎推理给出证明.
(1)、【定理证明】请根据教材内容,结合图①,写出证明过程.(2)、【定理应用】如图②,已知矩形ABCD中,AD=6,CD=4,点P在BC上从B向C移动,R、E、F分别是DC、AP、RP的中点,则EF= .(3)、【拓展提升】如图③,△ABC中,AB=12,BC=16,点D , E分别是AB , AC的中点,点F在DE上,且∠AFB=90°,则EF= .17. 中, , , 点为直线上一动点点不与 , 重合 , 以为边在右侧作菱形 , 使 , 连接 .
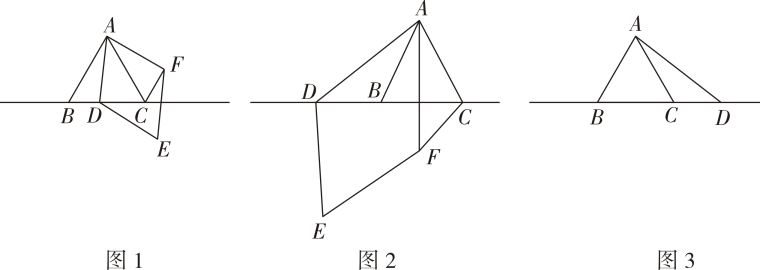 (1)、观察猜想:如图 , 当点在线段上时,
(1)、观察猜想:如图 , 当点在线段上时,
与的位置关系为: .
, , 之间的数量关系为:;(2)、数学思考:如图 , 当点在线段的延长线上时,结论 , 是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)、拓展延伸:如图 , 当点在线段的延长线上时,设与相交于点 , 若已知 , , 求的长.18. (1)、如图1,在矩形中,点 , 分别在边 , 上, , 垂足为点 . 求证: .(2)、【问题解决】
(1)、如图1,在矩形中,点 , 分别在边 , 上, , 垂足为点 . 求证: .(2)、【问题解决】如图2,在正方形中,点 , 分别在边 , 上, , 延长到点 , 使 , 连接 . 求证: .
(3)、【类比迁移】如图3,在菱形中,点 , 分别在边 , 上, , , , 求的长.