【提升版】浙教版数学九上4.4 两个三角形相似的判定 同步练习
试卷更新日期:2024-09-27 类型:同步测试
一、选择题
-
1. 如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
 A、
A、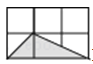 B、
B、 C、
C、 D、
D、 2. 下列图形不一定相似的是( )A、有一个角是120°的两个等腰三角形 B、有一个角是60°的两个等腰三角形 C、两个等腰直角三角形 D、有一个角是45°的两个等腰三角形3. 已知Rt△ABC,∠BCA=90°,过点C作一条射线,使其将△ABC分成两个相似的三角形.观察图中尺规作图的痕迹,作法正确的是( )
2. 下列图形不一定相似的是( )A、有一个角是120°的两个等腰三角形 B、有一个角是60°的两个等腰三角形 C、两个等腰直角三角形 D、有一个角是45°的两个等腰三角形3. 已知Rt△ABC,∠BCA=90°,过点C作一条射线,使其将△ABC分成两个相似的三角形.观察图中尺规作图的痕迹,作法正确的是( ) A、①② B、①③ C、②③ D、①②③4. 如图,点在的边上,添加一个条件,使得.以下是天翼和徍琛的做法.下列说法不正确的是( )
A、①② B、①③ C、②③ D、①②③4. 如图,点在的边上,添加一个条件,使得.以下是天翼和徍琛的做法.下列说法不正确的是( )
天翼的做法:添加条件.
证明: , , .(两组角对应相等的两个三角形相似)
徍琛的做法:添加条件.
证明: , ,
.(两组对应边成比例及一组对应角相等的两个三角形相似)
A、天翼的做法证明过程没有问题 B、徍琛的做法证明过程没有问题 C、天翼的做法添加的条件没有问题 D、徍琛的做法添加的条件有问题5. 如图,是边上一点,连接 , 则添加下列条件后,仍不能判定的是( ) A、 B、 C、 D、6. 如图,四个边长均为的正方形如图摆放,其中三个顶点位于坐标轴上,其中一个顶点在反比例函数的图象上,则的值为( )
A、 B、 C、 D、6. 如图,四个边长均为的正方形如图摆放,其中三个顶点位于坐标轴上,其中一个顶点在反比例函数的图象上,则的值为( ) A、 B、 C、 D、7. 如图, 为线段 上的一点, 与 交于点 , 与 交于点 交 于点 , 则下列结论中错误的是 ( )
A、 B、 C、 D、7. 如图, 为线段 上的一点, 与 交于点 , 与 交于点 交 于点 , 则下列结论中错误的是 ( ) A、△APD∽△PGD B、△APG∽△BFP C、△PCF∽△BCP D、△CGE∽△CBP8. 如图,在△ABD中,∠ABD=30°,∠A=105°,将△ABD沿BD翻折180°得到△CBD , 将线段DC绕点D顺时针旋转30°得到线段DF , 点E为AB的中点,连接EF , ED . 若EF=1,则△BED的面积是( )
A、△APD∽△PGD B、△APG∽△BFP C、△PCF∽△BCP D、△CGE∽△CBP8. 如图,在△ABD中,∠ABD=30°,∠A=105°,将△ABD沿BD翻折180°得到△CBD , 将线段DC绕点D顺时针旋转30°得到线段DF , 点E为AB的中点,连接EF , ED . 若EF=1,则△BED的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图, , 若 , 可添加的一个条件是(填写一个条件即可)
 10. 如图,这是由10个边长均为1的小正方形组成的图形,点P、X、Y是小正方形的顶点,Q为边上一点,连接 . 若平分这个图形的面积,则的值为 .
10. 如图,这是由10个边长均为1的小正方形组成的图形,点P、X、Y是小正方形的顶点,Q为边上一点,连接 . 若平分这个图形的面积,则的值为 . 11. 如图,有一个侧面为梯形的容器,高为 , 内部倒入高为的水.将一根长为的吸管如图放置,若有露出容器外,则吸管在水中部分的长度为 .
11. 如图,有一个侧面为梯形的容器,高为 , 内部倒入高为的水.将一根长为的吸管如图放置,若有露出容器外,则吸管在水中部分的长度为 . 12. 如图,正方形中,点为边上一点,点为左侧一点, , 若 , , 则 .
12. 如图,正方形中,点为边上一点,点为左侧一点, , 若 , , 则 .
三、解答题
-
13. 如图,△ABC的顶点均为网格中的格点.
 (1)、选择合适的格点(包括边界)为点D和点E,请画出一个△ADE,使△ADE∽△ABC(相似比不为1).(2)、证明:△ADE∽△ABC.14. 如图,AC、BD交于点E , ,且BD平分 .
(1)、选择合适的格点(包括边界)为点D和点E,请画出一个△ADE,使△ADE∽△ABC(相似比不为1).(2)、证明:△ADE∽△ABC.14. 如图,AC、BD交于点E , ,且BD平分 . (1)、求证: ∽ .(2)、若 , , ,求AB的长.15. 已知,在中, , 于点 , 是上一点,满足:;将绕点顺时针旋转 , 交于点 .
(1)、求证: ∽ .(2)、若 , , ,求AB的长.15. 已知,在中, , 于点 , 是上一点,满足:;将绕点顺时针旋转 , 交于点 . (1)、如图 ,
(1)、如图 ,(ⅰ)试说明:;
(ⅱ)若 , 请探究与的数量关系,并说明理由;
(2)、如图 , 若是线段的中点,求的值.16. 【问题提出】已知有两个Rt△ABC和Rt△A'B′C',其中∠C=∠C′=90°,∠A=60°,∠A′=45°. (1)、如图1,作线段CD,C′D′,分别交AB于点D,交A'B′于点D′,使得∠BCD=45°,∠B'C′D'=30°,问△BCD与△B'C′D',△ACD与△A′C′D′是否相似?并选择其中相似的一对三角形,说明理由.(2)、如图2,作线段AD,B'D′,分别交BC于点D,交A'C'于点D,若△ACD与△B′C′D′、△ABD与△A′B'D'均相似,求∠CAD,∠C'B'D′的度数.(3)、【拓展思考】已知任意两个不相似的直角三角形,能否分别作一条直线对其进行分割,使其中一个三角形所分割得到的两个三角形与另一个三角形所分割得到的两个三角形分别对应相似?如果可以,请直接画出一种分割示意图;如果不能,请说明理由.
(1)、如图1,作线段CD,C′D′,分别交AB于点D,交A'B′于点D′,使得∠BCD=45°,∠B'C′D'=30°,问△BCD与△B'C′D',△ACD与△A′C′D′是否相似?并选择其中相似的一对三角形,说明理由.(2)、如图2,作线段AD,B'D′,分别交BC于点D,交A'C'于点D,若△ACD与△B′C′D′、△ABD与△A′B'D'均相似,求∠CAD,∠C'B'D′的度数.(3)、【拓展思考】已知任意两个不相似的直角三角形,能否分别作一条直线对其进行分割,使其中一个三角形所分割得到的两个三角形与另一个三角形所分割得到的两个三角形分别对应相似?如果可以,请直接画出一种分割示意图;如果不能,请说明理由.