【培优版】浙教版数学九上4.2 由平行线截得的比例线段同步练习

试卷更新日期：2024-09-27 类型：同步测试

进入出卷网下载

一、选择题

1. 如图所示，在矩形ABCD中，AB=4，BC=3，E为DC的中点，连接AE交BD于点F，则BF的长为( )

A、 $\frac{8}{3}$ B、4 C、 $\frac{2}{3}$ D、 $\frac{10}{3}$

查看试题解析
2. 如图，等腰三角形ABC中， $A B = A C$ ，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点A、B及AC的中点M ， $B C ∥ x$ 轴，AB与y轴交于点N ．则 $\frac{A N}{A B}$ 的值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{2}{5}$

查看试题解析
3. 如图，在菱形 $A B C D$ 中，对角线交点为O ， E是 $A D$ 的中点，作 $E F ⊥ B D$ 于点F ， $E G ⊥ A C$ 于点G ，连接 $F G$ ．若 $A C = 10 ， B D = 24$ ，则 $F G$ 的长为（）

A、12 B、10 C、 $6.5$ D、5

查看试题解析
4. 如图，在 $△ A B C$ 中，点D在边AB上，过点D作 $D E ∥ B C$ ，交AC点E ．若 $A D = 2$ ， $B D = 3$ ，则 $\frac{A E}{A C}$ 的值是（）

A、 $\frac{2}{5}$ B、 $\frac{1}{2}$ C、 $\frac{3}{5}$ D、 $\frac{2}{3}$

查看试题解析
5. 如图，一次函数y=2x与反比例函数 $y = \frac{k}{x}$ 的图象相交于A，B两点，AC⊥AB交y轴于点C，BC的延长线交反比例函数的图象于点D，则 $\frac{C D}{B D}$ 的值为（）

A、2 B、3 C、 $\sqrt{3}$ D、 $\frac{4}{13}$

查看试题解析
6. 如图，在正方形ABCD中，E，F是对角线AC上的两点，且EF＝2AE＝2CF，连接DE并延长交AB于点M，连接DF并延长交BC于点N，连接MN，则 $\frac{S_{△ AMD}}{S_{△ M B N}} =$ （）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、1 D、 $\frac{1}{2}$

查看试题解析

二、填空题

7. 如图，正方形ABCD中，E为AB边上一点，过点E作EF⊥AB交对角线BD于点F.连接EC交BD于点G.取DF的中点H，并连接AH.若AH= $\sqrt{2}$ ，EG= $\frac{4}{7}$ ，则四边形AEFH的面积为.

查看试题解析
8. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，将 $△ A B C$ 绕点B顺时针旋转得到 $△ A^{'} B C^{'}$ ，其中点A ， C的对应点分别为点 $A^{'}$ ， $C^{'}$ ．当点 $C^{'}$ 落在 $A B$ 的延长线上时，连接 $C C^{'}$ ，交 $A^{'} B$ 于点P ，若 $A C ， B C$ 是方程 $x^{2} + 12 = 7 x$ 的两个实数根（ $A C > B C$ ），则 $△ A^{'} P C^{'}$ 的面积为．

查看试题解析
9. 如图， $△ A B F$ 、 $△ B C G$ 、 $△ C D H$ 、 $△ D A E$ 为四个全等的直角三角形， $B D$ 与 $C H$ 、 $E G$ 、 $A F$ 分别交于点 $M$ 、 $O$ 、 $N$ ，且满足 $D N = D C$ ，则两个阴影部分的面积和与四边形 $A B C D$ 面积的比值为．

查看试题解析
10. 如图，已知 $F$ 是 $△ A B C$ 内的一点， $F D ∥ B C$ ， $F E ∥ A B$ ，若 $▱ B D F E$ 的面积为2， $B D = \frac{1}{3} B A$ ， $B E = \frac{1}{4} B C$ ，则 $△ A B C$ 的面积是.

查看试题解析
11. 如图，在平行四边形ABCD中， $A B ⊥ A C$ ， $A B = 3$ ， $A C = 4$ ，分别以A，C为圆心，大于 $\frac{1}{2} A C$ 的长为半径画弧，两弧相交于点M，N，过M，N两点作直线，与BC交于点E，与AD交于点F，连接AE，CF，则四边形AECF的周长为.

查看试题解析
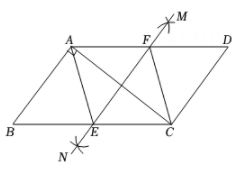12. 如图，AB∥CD ， AD与BC相交于点O ．若 $\frac{B O}{O C} = \frac{2}{3}$ ， AD＝15，则AO的长为．

查看试题解析

三、解答题

13. 如图．在△ABC中，E是AB的中点，D是AC上的一点，且AD：DC=2：3，BD与CE交于F，S_△_AB_C=40，求S_AEFD ．

查看试题解析
14. 如图1， $△ A B C$ 是等腰直角三角形， $∠ A C B = 90 ° ， A C = B C$ ，先将边 $B C$ 沿过点B的直线l对折得到 $B D$ ，连接 $C D$ ，然后以 $C D$ 为边在左侧作 $△ C D E$ ，其中 $∠ C D E = 90 °$ ， $C D = D E$ ， $B D$ 与 $C E$ 交于点F，连接 $B E$ ， $A D$ ．

(1)、求证： $△ A C D ≌ △ B D E$ ；

(2)、如图2，当点D在 $△ A B C$ 的斜边 $A B$ 上时，请直接写出用 $B C ， B E$ 表示 $A B$ 的关系式；

(3)、如图3，当点D在 $△ A B C$ 的内部时，若点F为 $B D$ 的中点，且 $△ A C D$ 的面积为10，求 $△ C D F$ 的面积．

查看试题解析
15. 如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）.DE∥AB交AC于点F，CE∥AM，连结AE.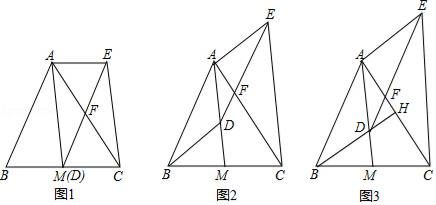

(1)、如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；

(2)、如图2，当点D不与M重合时，（1）中的结论还成立吗？请说明理由.

(3)、如图3，延长BD交AC于点H，若BH⊥AC，且BH=AM.
①求∠CAM的度数；

②当FH= $\sqrt{3}$ ，DM=4时，求DH的长.

查看试题解析
16. 如图，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与直线 $y = 4 x$ 交于点 $D (1 ， m)$ ，在射线 $O D$ 上取一点 $A$ ，过点 $A$ 作 $y$ 轴的垂线分别交反比例函数的图象和 $y$ 轴于点 $B$ 和点 $C$ ．

(1)、求反比例函数的解析式；

(2)、当 $A D = 2 O D$ 时，
①求点 $A$ 的坐标；
②求 $△ O B D$ 的面积．

查看试题解析

四、实践探究题

17. 垂中平行四边形的定义如下：在平行四边形中，过一个顶点作关于不相邻的两个顶点的对角线的垂线交平行四边形的一条边，若交点是这条边的中点，则该平行四边形是 “垂中平行四边形”.

(1)、如图所示，四边形 $A B C D$ 为 “垂中平行四边形”， $A F = \sqrt{5}, C E = 2$ ，则 $A E =$ ； $A B =$ ；

(2)、如图 2，若四边形 $A B C D$ 为 “垂中平行四边形”，且 $A B = B D$ ，猜想 $A F$ 与 $C D$ 的关系，并说明理由；

(3)、①如图 3 所示，在 $△ A B C$ 中， $B E = 5, C E = 2 A E = 12, B E ⊥ A C$ 交 $A C$ 于点 $E$ ，请画出以 $B C$ 为边的垂中平行四边形，要求：点 $A$ 在垂中平行四边形的一条边上 (温馨提示：不限作图工具)；
②若 $△ A B C$ 关于直线 $A C$ 对称得到 $△ A B^{^{'}} C$ ，连接 $C B^{^{'}}$ ，作射线 $C B^{^{'}}$ 交①中所画平行四边形的边于点 $P$ ，连接 $P E$ ，请直接写出 $P E$ 的值.

查看试题解析

【培优版】浙教版数学九上4.2 由平行线截得的比例线段 同步练习

一、选择题

二、填空题

三、解答题

四、实践探究题

【培优版】浙教版数学九上4.2 由平行线截得的比例线段同步练习