【提升版】浙教版数学九上4.2 由平行线截得的比例线段 同步练习
试卷更新日期:2024-09-27 类型:同步测试
一、选择题
-
1. 如图,在 中, , , , ,则 的长为( )
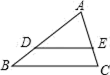 A、6 B、7 C、8 D、92. 如图,已知 , 它们依次交直线、于点、、和点、、 , 如果:: , , 那么的长等于( )
A、6 B、7 C、8 D、92. 如图,已知 , 它们依次交直线、于点、、和点、、 , 如果:: , , 那么的长等于( ) A、 B、 C、 D、3. 如图, , 若 , , , 则DF的长度是( )
A、 B、 C、 D、3. 如图, , 若 , , , 则DF的长度是( ) A、6 B、8 C、10 D、124. 如图,已知AD∥BE∥CF,若AB=2BC,DF=12,则EF的长为( )
A、6 B、8 C、10 D、124. 如图,已知AD∥BE∥CF,若AB=2BC,DF=12,则EF的长为( ) A、2 B、4 C、6 D、85. 中,D、E分别是边、上的点,下列各式中,能判断的是( )A、 B、 C、 D、6. 一段加固后的护栏如图所示,该护栏竖直部分是由等距(任意相邻两根木条之间的距离相等)且平行的木条构成.已知AC=50cm,则BC的长度为( )
A、2 B、4 C、6 D、85. 中,D、E分别是边、上的点,下列各式中,能判断的是( )A、 B、 C、 D、6. 一段加固后的护栏如图所示,该护栏竖直部分是由等距(任意相邻两根木条之间的距离相等)且平行的木条构成.已知AC=50cm,则BC的长度为( )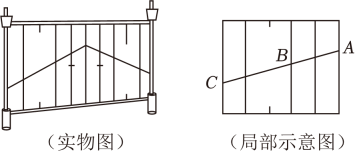 A、20cm B、25cm C、30cm D、cm7. 如图,直线 , 直线a , b相交于点 , 且与分别相交于点B , C和点D , E . 若 , , 则的长为( )
A、20cm B、25cm C、30cm D、cm7. 如图,直线 , 直线a , b相交于点 , 且与分别相交于点B , C和点D , E . 若 , , 则的长为( ) A、 B、 C、 D、8. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( )
A、 B、 C、 D、8. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、2
A、 B、1 C、 D、2二、填空题
-
9. 如图, , 则的长是 .
 10. 如图,点D、E是边 上的点, , 连接 , 交点为F , , 那么的值是 .
10. 如图,点D、E是边 上的点, , 连接 , 交点为F , , 那么的值是 . 11. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点、、都在横格线上若线段 , 则线段 .
11. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点、、都在横格线上若线段 , 则线段 .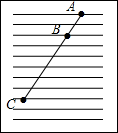 12. 如图,在边长为1的正方形网格中,点A , B均在格点上.
12. 如图,在边长为1的正方形网格中,点A , B均在格点上.
⑴的长为;
⑵请只用无刻度的直尺,在如图所示的网格中,画出以为边的矩形 , 使其面积为 , 并简要说明点C , D的位置是如何找到的(不用证明): .
三、解答题
-
13. 如图, , 直线 , 交于点 , 且分别与直线 , , 交于点、、和点、、 , 已知 , , , , 求的长度是?
 14. 如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
14. 如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
四、综合题
-
15. 如图,已知AD∥BE∥CF,它们依次交直线l1 , l2 , 于点A,B,C和点D,E,F.
 (1)、如果AB=6,BC=8,DF=7,求EF的长.(2)、如果AB:AC=2:5,EF=9,线段x是线段DE和线段DF的比例中项,求x的值.16. 如图,已知 , 与相交于点E,点F在线段上, , .
(1)、如果AB=6,BC=8,DF=7,求EF的长.(2)、如果AB:AC=2:5,EF=9,线段x是线段DE和线段DF的比例中项,求x的值.16. 如图,已知 , 与相交于点E,点F在线段上, , . (1)、求证:;(2)、求 .
(1)、求证:;(2)、求 .五、实践探究题
-
17. 综合与实践课本再现
思考:我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?可以发现并证明菱形的一个判定定理:对角线互相垂直的平行四边形是菱形.

定理证明:为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.
已知:在中,对角线 , 垂足为O.
求证:是菱形.
证明:四边形是平行四边形,
又∵、垂足为O ,
是的垂直平分线,
▲ 是菱形.
(1)、上述证明定理过程中的横线上填的内容是;(2)、知识应用:如图2,在中,对角线和相交于点O , , , .①求证:是菱形;
②延长至点E , 连接交于点F , 若 , 求的值.